图解LeetCode——48. 旋转图像

news2024/12/25 9:03:25

一、题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

二、示例

2.1> 示例 1：

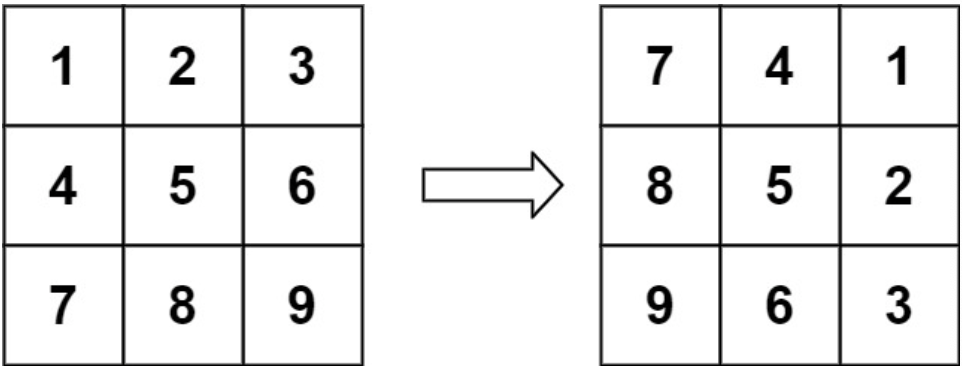
【输入】matrix = [[1,2,3],[4,5,6],[7,8,9]]
【输出】[[7,4,1],[8,5,2],[9,6,3]]

2.2> 示例 2：

【输入】matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
【输出】[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

三、解题思路

根据题目描述，我们要将题目给出的二维矩阵matrix进行顺时针90度的旋转，然后返回旋转后matrix数组即可。其中，比较容易想到就是先创建一个相同大小的二维矩阵matrix_new，然后执行如下步骤：

【步骤1】遍历二维矩阵matrix第1行的时候，就将其赋值为matrix_new的最后1列；
【步骤2】遍历二维矩阵matrix第2行的时候，就将其赋值为matrix_new的倒数第2列；
【步骤2】遍历二维矩阵matrix第3行的时候，就将其赋值为matrix_new的倒数第3列；
以此类推……

但是，题目有一个要求，就是请不要使用另一个矩阵来旋转图形，所以上面的解法就不适合去解答这道题了。那么我们还有什么其他的解法呢？我们其实可以采用如下两个步骤移动二维矩阵：

【步骤1】将matrix二维矩阵进行上下互换；
【步骤2】将matrix二维矩阵进行对角互换；

经过上面两个步骤，我们就可以实现将matrix二维矩阵顺时针旋转90度。为了便于理解，我们以输入matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]为例，来看一下具体的操作流程。具体请见下图所示：

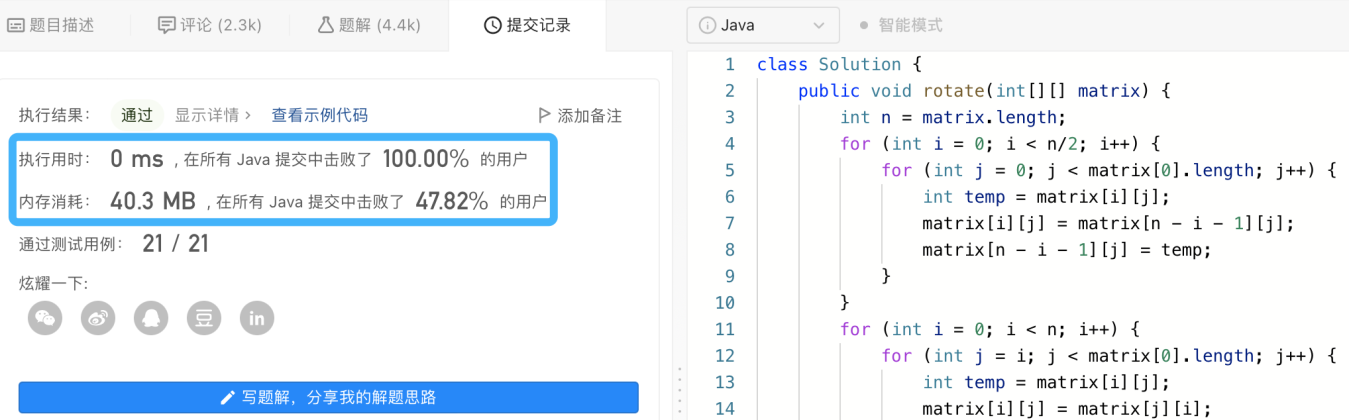
四、代码实现

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n/2; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = i; j < matrix[0].length; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }    
        }
    }
}