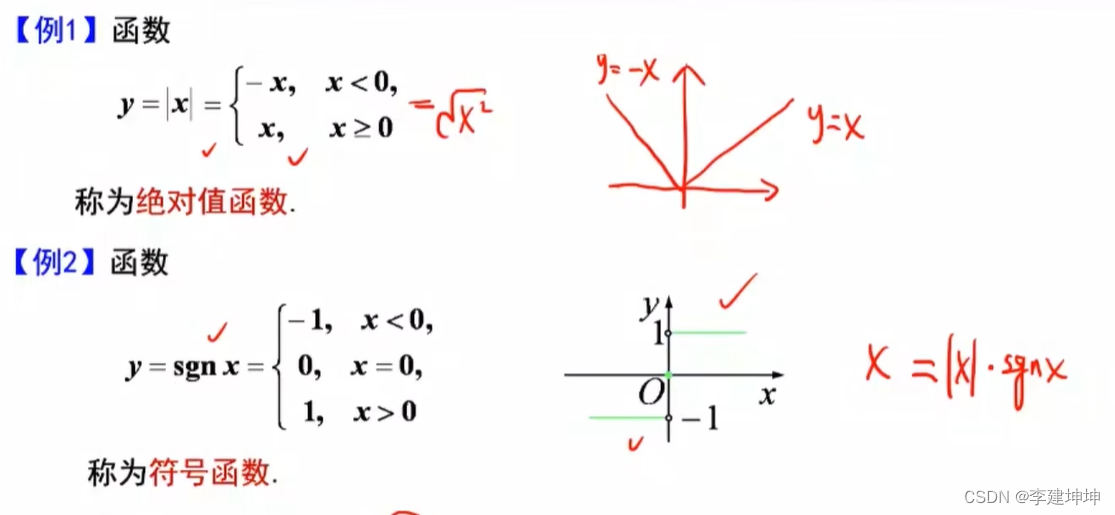
常见的函数

取整函数的基本性质

函数的有界性

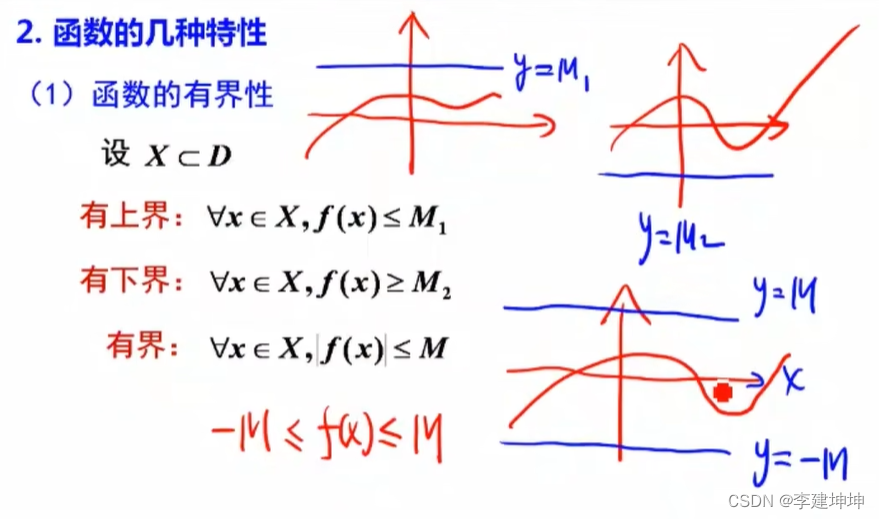
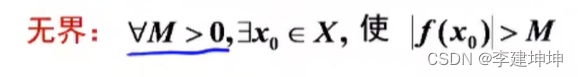
例题

sinx 是从-1到1的，但是x是无界的

遇到这种带sin的，就要试着取特殊值，让它为1或者为0

函数的单调性

函数的奇偶性

函数的周期性

举例

数学中Q表示有理数集，下面那个符号表示无理数集
这个函数是周期函数，但是没有最小正周期

这个也一样，是周期函数，但是没有最小正周期，任何一个常数都是它的周期

反函数

复合函数

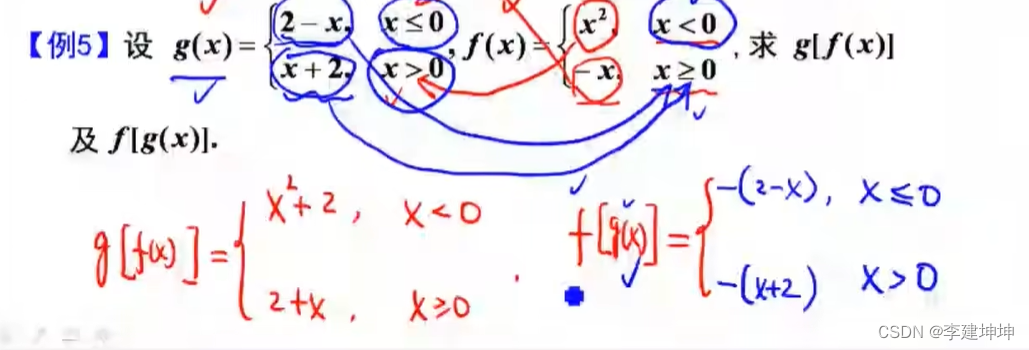
函数的运算

例题

初等函数

比如：


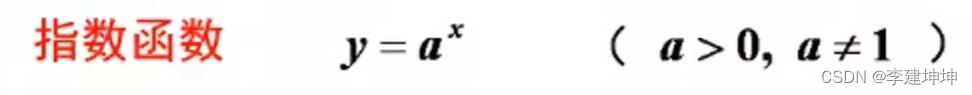
比如：

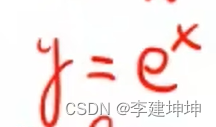
图像是这样的

值域是


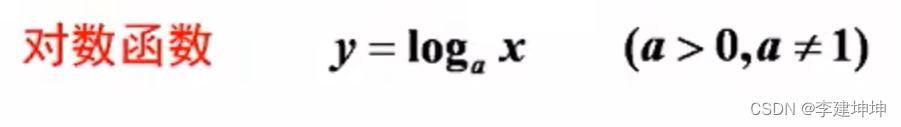
常见的是：

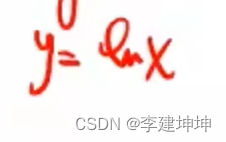
图像是这样的

值域是（-∞，+∞），单调增，经过（1，0）

y = sin x 和 y = cos x 周期是2Π，是有界函数
y = tanx 和 y = cot x 周期是Π ，是无界函数

其中最常见的是 y = arctan x ,图像如下：

基本概念

函数小结

作业

课后习题

1.根号下≥0
2.分母不能为0
3.分母不能为0且根号下大于等于0
4.分母不能为0且根号下大于等于0
5.根号下大于等于0 ，注意 sin 里面没有对定义域的限制
6.反斜杠""是一种集合运算符号，集合U和A的相对差集，符号为U \ A，是在集合U中，但不在集合A中的所有元素，相对差集{1，2，3} \ {2，3，4} 为{1} ，而相对差集{2，3，4} \ {1，2，3} 为{4}
tan x 的值域为（-Π/2 +kΠ，Π/2 + kΠ）
7.arcsin x 的值域为 [-1,1]
8.根号下≥0，分母不为0
9.

10.分母不能为0

1.虽然化简之后相同，但是定义域不同

2.值域不一样，一个是R,一个≥0
3.相同，因为开立方根的定义域是全体实数
4.