前言

链表是面试中常见的一类题。分为单链表，双向链表，循环链表等八类。

在基础部分考察单链表较多，涉及：有序链表的合并、链表的逆置、链表的分割、找链表的中间结点。

在进阶方面一种不可少的类型：链表带环问题。

本文就深入探讨如何判断链表是否带环，如何找到环的入口点及其证明。

一、什么是环形链表

定义：链表的tail结点的next不为空，指向该链表的某个结点。则改链表带环。

另一个定义：如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

如下图所示：第3个结点的next指向第1个结点。这称该链表带环。

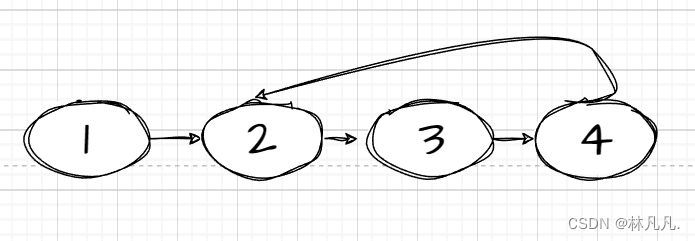
通过链表带环的性质，可以得到：

带环链表不能连续遍历。

如果tail结点的next指向head结点，这时链表为循环链表。

二、判断链表是否带环

方法：快慢指针

思路：fast(快指针)和slow(慢指针)同时从head起点开始走，fast一次走俩步，slow一次走一步。

如果没有环，fast会走到NULL。如果存在环，fast会先进入环，然后在环里一直走（甚至可能多绕几次圈），直到slow进环。此时fast和slow同时在环中，fast开始追slow。

下面来看一下代码

bool hasCycle(struct ListNode *head) {
    if(head==NULL)
    {
        return false;
    }
    struct ListNode*fast=head,*slow=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast)
        {
            return true;
        }
    }
    return false;
}

相信写出这样的代码对于大多数人来说并不是问题

但是通常面试官会接着往下问这俩个问题。

三、（问题1）slow和fast一定会相遇吗？

答案：slow走一步fast走俩步，一定会相遇。

证明：

fast走的路程是slow的俩倍，所以fast会先进环，slow一步一步往前走，fast在环里走。

假设slow进环时与fast的距离是N

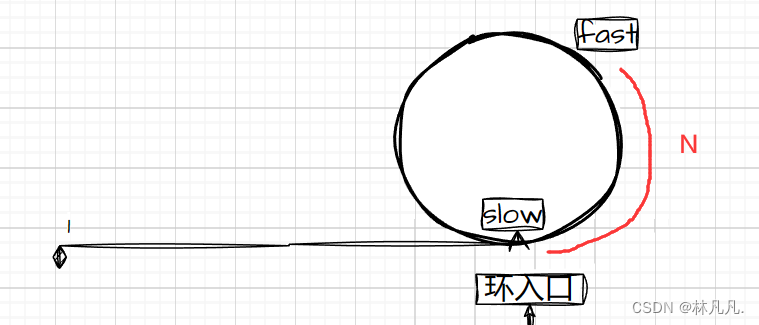
fast开始追slow,fast一次走俩步，slow一次走一步，它们的路程差为1步，每次减小1。

它们之间的距离就会从N、N-1、N-2.......4、2直到0,为0时，就是相遇。

所以fast一次走两步，slow一次走一步，一定会相遇。

四、（问题2）fast一次走3/4/n步，还会相遇吗？

答案：不一定

1.fast一次走3步

假设slow进环时与fast的距离是N，路程差为2，每次减少2

N为偶数时 N为奇数时

N-2 N-2

N-4 N-4

N-6 N-6

..... ......

4 3

2 1

0 -1

当N为偶数时，fast一定能追上slow

当N为奇数时，fast会错过slow，再次追击

假设链表环的长度是C

fast与slow的距离为-1，就是fast在slow前一步。

可以理解为初始时刻，fast与slow的距离为C-1。将slow看为参照物，fast就是每次走俩步，追击slow。能否遇到，还是要分C-1为奇数还是偶数。

C-1是偶数 C-1是奇数

C-1-(2) C-1-(2)

C-1-(4) C-1-(4)

C-1-(6) C-1-(6)

....... ........

2 1

0 -1

C-1是奇数时，最后余下-1，意味着fast第二次经过slow,之后它们永远不会相遇。

错过永远不会再遇到。

2.fast一次走4步

假设slow进环时与fast相差N的距离,每次距离减少3步