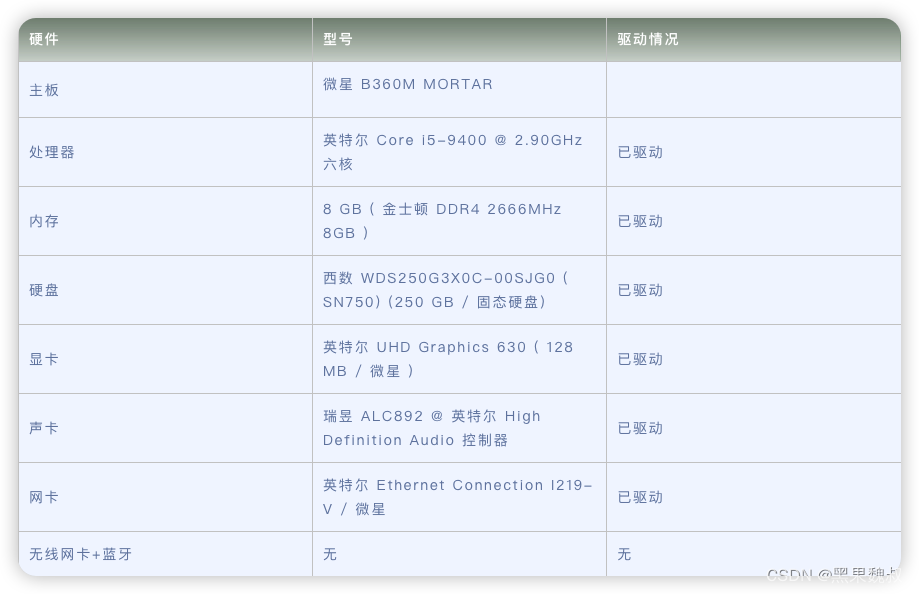
目录
- 1引入情境
- 2 形式化描述
- 2-1递归结构
- 2-2 一次划分
- 2-3 C++实现
- 3 在工程中的改进
- 3-1 处理重复元素
- 双向划分
- 三路划分
- C++ 实现
- 3-2 最差情况的改进
- 三点中值法
- 随机选择pivot
- 短序列切回插入排序
- 4 全部改进技术加持
1引入情境

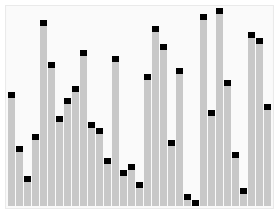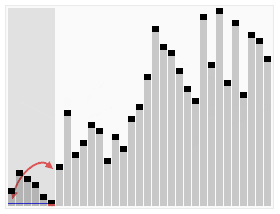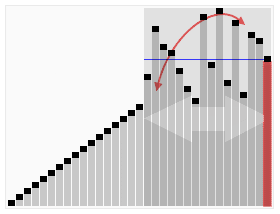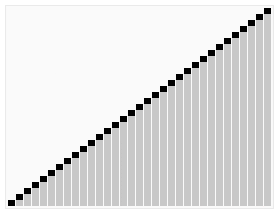
- 以大雄为中心,比他高度的到右边,比他低的到左边。
- 分好之后左侧的每个人也重复第一步,右侧也重复第一步。
把大雄的身高为枢纽,如果下图中的紫色横线。每次从左右两侧找的不满足条件的,即在大雄左边却比大雄高,在大雄右边却比大雄低,交换两者,不断递归,最后有序。
2 形式化描述
2-1递归结构
整体是函数递归的方式对序列L排序:
s
o
r
t
(
L
)
=
{
s
o
r
t
(
{
x
∣
x
∈
L
′
,
x
≤
l
1
}
)
∪
{
l
1
}
∪
s
o
r
t
(
{
x
∣
x
∈
L
′
,
x
>
l
1
}
)
,
L不空
∅
,
L为空集
sort(L) = \begin{cases} sort(\{ x| x\in L^\prime ,x \leq l_1 \} )\cup \{l_1\}\cup sort(\{x| x\in L^\prime ,x > l_1 \}), & \text{L不空} \\ \emptyset, & \text {L为空集 } \end{cases}
sort(L)={sort({x∣x∈L′,x≤l1})∪{l1}∪sort({x∣x∈L′,x>l1}),∅,L不空L为空集
-
l
1
l_1
l1 是上图的紫色横线,即分割点或枢纽
pivot,通常取队列的第一个数据。注意,pivot的选择会直接影响到排序的效率。 - L ′ L^\prime L′是队列去除枢纽值 l 1 l_1 l1后的部分。
- 比较条件为小于等于,即单调非递减的顺序排序。
利用python 可以基本如上公式实现快速排序。
def sort(L):
if L == []:
return []
pivot = L[0]
aL = sort(filter(lambda x:x<=pivot,L[1:]))
bL = sort(filter(lambda x:x >pivot,L[1:]))
return aL+[pivot]+bL
注意到,这里为了获得比枢纽pivot大的元素遍历了一次(filter),同样的为了获得比枢纽pivot小的元素又遍历了一次(filter),这个过程可以合并为一次划分过程,就是最上面图示里的交换。
2-2 一次划分
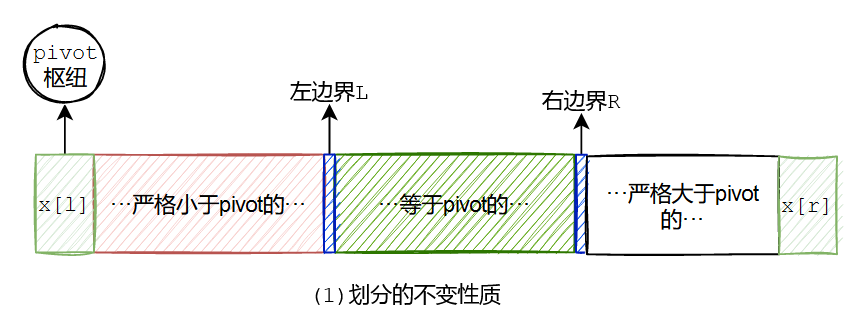
对(Nico Lomuto提出的)划分方法说明具体可参照下图:

- 选取最左边第一个元素 x l x_l xl为枢纽pivot,当划分结束,pivot会被放到分界线位置,作为不大于pivot和大于它的枢纽。
- 大于pivot的部分被显式的下标
L,R所确定,即区间[L,R]内的元素都大于pivot,记为断言P。 - 划分开始,L=R,即大于pivot的区间初始化为空集。之后,R向右移动,如果
x
R
>
p
i
v
o
t
x_R>pivot
xR>pivot即满足断言P故R继续向右移动;如果
x
R
≤
p
i
v
o
t
x_R\leq pivot
xR≤pivot,不满足断言P,需要将
x
R
x_R
xR移出区间
[L,R],具体来说就是交换 x L + 1 x_{L+1} xL+1和 x R x_R xR,即可保证[l,L)内的元素不大于pivot。 - 划分结束时,L指向边界,需要把pivot和当前值交换,划分后即得到不大于枢纽的
[l,L)与大于枢纽的[L,r]。
伪代码说明
function partitio(A,l,r):
p = A[l] #枢纽pivot
L = l # 左侧标记
for R from l+1 to r do # 迭代未处理的元素
if not (p < A[R]) then
L=L+1
swap(A[L],A[R])
swap(A[L],A[l])
return L+1 #返回划分位置
2-3 C++实现
代码将断言P封装为独立的函数,然后作为参数传入划分函数中。
#include<iostream>
#include<vector>
#include<functional> //函数指针包装
using namespace std;
using Array=vector<int>;
using Assertion=function<bool(int,int)>;
//断言 当前值大于枢纽
bool P(int now,int pivot){
return pivot<now;
}
int partition(Array &A,int l,int r,Assertion P){
int p=A[l];
int L=l,R;
for(R=l+1;R<=r;++R){
if(!P(A[R],p)){ //不满足断言P需要交换
++L;
swap(A[R],A[L]);
}
}
swap(A[l],A[L]);
return L+1;
}
void qsort(Array &A,int l,int r){
if(l<r){
int p=partition(A,l,r,P);
qsort(A,l,p-1);
qsort(A,p,r);//p是枢纽的下一个位置
}
}
#define see(x) cout<<(x)<<endl
void test(){
Array A{5,9,2,6,1};
// test partition
// see(partition(A,0,4));
//test qsort
qsort(A,0,A.size()-1);
for(auto &x:A){
see(x);
}
}
int main(){
test();
return 0;
}
3 在工程中的改进
考虑不同情况下的性能:
- 理想情况下,每次都能平均划分成差不多的两段,即分lgN次最后得到一棵平衡二叉树,N个单一元素为叶子,总处理时间O(N);层层加起来,即
O(NlgN)。 - 最坏情况下二叉树退化为链表,即
O
(
N
2
)
O(N^2)
O(N2)。
- 其中一种情况是大部分元素都相同,上述的划分方法会对相同值也做无效交换,效率降低;
- 或序列本来有序,因此每次划分得到左边(或右边)是空集,相当于无效划分。
3-1 处理重复元素
如下图,把二分划分变为三分划分,将重复元素(即等于枢纽pivot)的值作为一个集合E。为方便理解三路划分的思路,需要先了解一下经典的双向划分作为基础。
双向划分
再把开头的图拉上来,注意到红色双箭头表示有两个指针分别从当前段的头尾出发,向中间收缩,等找到一对儿违反断言X:左侧
≤
\leq
≤ pivot
<
<
<右侧的数据就交换左右的值。

// 注意 数组范围是A[l,r]
void qsort1(Array &A,int l,int r){
int i,j,pivot;
if(l<r-1){
pivot=i=l;
j=r+1;//为了凑下面形式一致用--j得到真实数据
while(1){
while(i<r && A[++i]<A[pivot]);
while(j>=l && A[pivot]<A[--j]);
if(i>j) break;
swap(A[i],A[j]);
}
swap(A[pivot],A[j]);
qsort1(A,l,j);
qsort1(A,i,r);
}
}
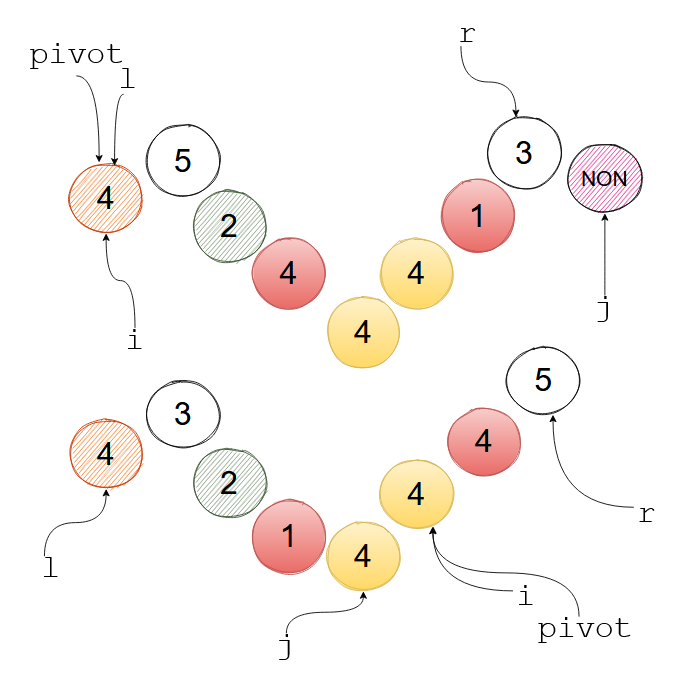
极端情况下,所有数字都相同,会发生N/2次不必要的交换,因为划分是平衡的,故总体性能还是O(NlgN)。这里举一个划分一次的实际用来说明i、 pivot 、j实际的位置含义。注意到,这种划分跳过了本来就正确的元素2,不进行交换,比Nick Lomuto 提出的一次划分减少了交换次数。
- 同色的气球发生了交换
- 划分完成后,
pivot并不在边界上 - 注意到 j j j 最终在 i i i的左侧
#include<iostream>
#include<vector>
using namespace std;
using Array=vector<int>;
void qsort1(Array &A,int l,int r){
int i,j,pivot;
if(l<r-1){
pivot=i=l;
j=r+1;
while(1){
while(i<r && A[++i]<A[pivot]);
while(j>=l && A[pivot]<A[--j]);
if(i>j) break;
//cout<<i<<" <--> "<<j<<endl;
swap(A[i],A[j]);
}
//cout<<"final "<<pivot<<" "<<j<<endl;
// for(auto& x:A){
// cout<<x<<" ";
//}
//cout<<endl;
swap(A[pivot],A[j]);
qsort1(A,l,j);
qsort1(A,i,r);
}
}
#define see(x) cout<<(x)<<endl
void test(){
Array A{4,5,2,4,4,4,1,3};
//test qsort
qsort1(A,0,A.size()-1);
for(auto &x:A){
see(x);
}
}
int main(){
test();
return 0;
}
三路划分
如下图所示,三路划分有几个特点:
- i 和 j 指针和二路划分的动作相似,从两头向中间,寻找不满足断言Y:左侧 < < < pivot < < <右侧的一对 x i x_i xi 和 x j x_j xj。
- 当
x
i
≥
p
i
v
o
t
x_i \geq pivot
xi≥pivot 并且
x
j
≤
p
i
v
o
t
x_j \leq pivot
xj≤pivot 时,有个分类讨论。
- 当 i < j i < j i<j时,先交换 x j x_j xj 和 x i x_i xi,否则退出。
- 当存在某值等于 p i v o t pivot pivot,需要交换 s w a p ( x p , x i ) swap(x_p, x_i) swap(xp,xi),或 s w a p ( x j , x q ) swap(x_j,x_q) swap(xj,xq),保证等于pivot的元素在两边。 - 划分结束之前需要把所有等于pivot的元素从两边交换到中间,O(重复元素个数),之后对严格大于、严格小于的部分递归排序。

伪代码说明:
# 数组A[l,r),r取不到
function Sort(A,l,r):
if r-l >1 then # 至少有1个数据
i=l, j=r
p=l, q=r
pivot= A[l] # 以上初始化
loop
# 先忽略下标检查
repeat
i=i+1
until A[i]>= pivot
repeat
j=j-1
until A[j]<= pivot # 以上寻找非断言Y的数据对
if j<=i then # 注意,取等也要退出
break
swap(A[j],A[i])
if A[i]==pivot then
p=p+1
swap(A[p],A[i])
if A[j]==pivot then
q= q -1
swap(A[q],A[j])
#loop end
if i==j and A[i]==pivot then #特殊情况
j= j-1, i=i+1
# 移动到中间,注意此刻j在i的左边
for k from l to p do
swap(A[k],A[j])
j=j-1
for k from r-1 down-to q do
swap(A[k],A[i])
i=i+1
Sort(A,l,j+1)
Sort(A,i,r)
C++ 实现
void qsort2(Array A,int l,int r){
// A[l,r),注意r是取不到的
int i, j, k, p, q, pivot;
if (l < r - 1)
{
i = p = l;
j = q = r;
pivot = A[l];
while (1)
{
while (i < r && A[++i] < pivot)
; //先检查下标
while (j >= l && pivot < A[--j])
;
if (j <= i)
break;
swap(A[i], A[j]);
// 多了移动相同值
if (A[i] == pivot)
{
++p;
swap(A[i], A[p]);
}
if (A[j] == pivot)
{
--q;
swap(A[j], A[q]);
}
}
// 确认j在i的左边
if (i == j && A[i] == pivot)
{
--j;
++i;
}
for (k = l, k <= p; ++k, --j)
{
swap(A[k], A[j]);
}
for (k = u - 1; k >= q; --k, ++i)
{
swap(A[k], A[i]);
}
qsort2(A, l, j + 1);
qsort2(A, i, r);
}
}
3-2 最差情况的改进
假定 x 1 x_1 x1到 x n x_n xn自然有序,最差情况:
- 有序,还选取第一个数作为pivot,划分的结果总包含一个空集。
- { x n , x 1 , x n − 1 , x 2 , . . . } \{x_n,x_1,x_{n-1},x_2,...\} {xn,x1,xn−1,x2,...},重复的Z字形,选第一个做pivot还是补平衡,一边可能只有一个元素;
- { x m , x m − 1 , . . . , x 1 , x m + 1 , x m + 2 , . . . , x n } \{x_m,x_{m-1},...,x_1,x_{m+1},x_{m+2},...,x_n\} {xm,xm−1,...,x1,xm+1,xm+2,...,xn}只有第一次平衡,其他都是不平衡的。
可以发现问题出在对pivot的选择有局限性。怎么选择pivot来实现平衡的划分是一个关键。
三点中值法
一种抽样的方法是检查,头,尾巴,中间的元素,然后选出其中的中位数作为pivot,即可保证最短序列至少有一个元素。
注意,计算中间值下标,用 L + R L+R L+R可能会溢出,建议用 L + ( R − L ) / 2 L+(R-L)/2 L+(R−L)/2。
怎么求中位数呢?
- 三次比较,ABC来确定
- 交换方法,使得最小值在左边,中值在中间,大值在右边。
# 采用交换的方式来实现
function Sort(A,l,r):
if r-l > 1 then
m = (l+r)/2 # 小心溢出问题
if A[m] < A[l] then # 保证 A[l]<=A[m]
swap(A[l],A[m])
if A[u-1]<A[l] then # 保证A[l]<=A[r-1]
swap(A[l],A[u-1])
if A[r-1]<A[m] then # 保证 A[m]<=A[r-1]
swap(A[m],A[r-1])
swap(A[m],A[l]) # 把选出来的中值放到首个,默认作为partition函数枢纽
(i,j) <- partition(A,l,r)
Sort(A,l,i)
Sort(A,j,r)
随机选择pivot
很简单,就是随机选一个值和左边的第一个值交换。见命令式函数的伪代码描述:
# A[l,r) 末尾r取不到
function Sort(A,l,r)
if r-l > 1 then
swap(A[l],A[Random(l,r)]) # 随机选择元素,放到首位
(i,j) = partition(A,l,r)
Sort(A,l,i)
Sort(A,j,r)
注意到,纯函数式编程中,列表的底层是单向链表,没有简单的方法可以实现纯函数式的随机快速排序。
短序列切回插入排序
这个更简单,因为Robert Sedgewick 观察到,当序列较短时,快速排序引入的额外代价比较明显,此时插入排序反而更快。即如果序列的元素个数少于Cut-Off 就转入插入排序。其中Cut-Off可以由对特定的数据做具体实验获得。
function Sort(A,l,r):
if r-l >Cut-Off then
Quick-Sort(A,l,r)
else
Insertion-Sort(A,l,r);
4 全部改进技术加持
测试后可知,对int数当序列长度接近23左右时,插入排序更好,且该结果随着整体元素的变大而有所波动。
#include<iostream>
#include<vector>
#include<functional> //函数指针包装
#include<chrono> //测试运行时间
#include<ctime> // 随机数数组
using namespace std;
// 模拟模板类
using Key=int;
using Array=vector<Key>;
using Assertion=function<bool(int,int)>; //断言函数指针
// 用于测试运行的时间
using Time=chrono::steady_clock;
using Duration=chrono::duration<double>;
using SortFunc=function<void(Array&,int ,int)>; //排序的函数指针
double getRunTime(SortFunc run,Array &A,int l,int r){
auto beforeTime = Time::now();
run(A,l,r);
auto afterTime = Time::now();
// 运行多少秒
return Duration(afterTime - beforeTime).count();
}
class Sort
{
// 默认A[l,r)右边界一律取不到;(r-l)即数组长度。
private:
static const size_t CUT_OFF=24;
static void get_pivot(Array &A, int l, int r);//三点中值法求pivot
public:
static void insert_sort(Array &A,int l,int r);
static void quick_sort(Array &A,int l,int r);
static void sort(Array &A,int l,int r){
if(r-l>CUT_OFF){
quick_sort(A,l,r);
}else{
insert_sort(A,l,r);
}
}
};
// 三点中值法,并将中值放到A[l],划分默认以A[l]为pivot
void Sort::get_pivot(Array &A, int l, int r){
int m=l+(r-l)/2;
if(A[m]<A[l]){ //保证A[l]<=A[m]
swap(A[m],A[l]);
}
if(A[r-1]<A[l]){ //保证A[l]<=A[r-1]
swap(A[r-1],A[l]);
}
if(A[r-1]<A[m]){ //保证A[m]<=A[r-1]
swap(A[r-1],A[m]);
}
swap(A[l],A[m]);
}
//三路划分+三点中值法
void Sort::quick_sort(Array &A, int l, int r)
{
// A[l,r),注意r是取不到的
int i, j, k, p, q, pivot;
if (l < r - 1)
{
i = p = l;
j = q = r;
get_pivot(A,l,r);//三点中值法
pivot = A[l];
while (1)
{
while (i < r && A[++i] < pivot)
;
while (j >= l && pivot < A[--j])
;
if (j <= i)
break;
swap(A[i], A[j]);
// 多了移动相同值
if (A[i] == pivot)
{
++p;
swap(A[i], A[p]);
}
if (A[j] == pivot)
{
--q;
swap(A[j], A[q]);
}
}
// 包装j在i的左边
if (i == j && A[i] == pivot)
{
--j;
++i;
}
for (k = l; k <= p; ++k, --j)
{
swap(A[k], A[j]);
}
for (k = r - 1; k >= q; --k, ++i)
{
swap(A[k], A[i]);
}
quick_sort(A, l, j + 1);
quick_sort(A, i, r);
}
}
void Sort::insert_sort(Array &A, int l, int r){
if (r - l > 1)
{
for (int j = l + 1; j < r; j++)
{
int key = A[j];
int i = j - 1;
while (i >= 0 && A[i] > key)
{
A[i + 1] = A[i];
i--;
}
A[i + 1] = key;
}
}
}
//生成范围在l~r的随机数
void random_array(Array &A,int l,int r)
{
srand(time(0)); //设置时间种子
for(int i=0;i<A.size();i++){
A[i]=rand()%(r-l+1)+l;
}
}
// 用于测试真实的cut-off的值
void test_cutoff(size_t cutoff)
{
//随机数组
Array A(cutoff);
const size_t MAX=992453499;
random_array(A, 0, MAX);
// 测时间
Sort obj;
auto insert_time = getRunTime(obj.insert_sort,A,0,A.size());
auto qsort_time = getRunTime(obj.quick_sort,A,0,A.size());
cout<<"MAX = "<<MAX <<" CUT-OFF = "<<cutoff<<" ";
if(insert_time<qsort_time){
cout<<"insert better"<<endl;
}else{
cout<<"qsort better"<<endl;
}
} // MAX = 992453499 CUT-OFF = 24 insert better
#define see(x) cout<<(x)<<endl
void test(){
Sort obj;
Array A{4,5,2,4,4,4,1,3};
obj.sort(A,0,A.size());
obj.insert_sort(A,0,A.size());
obj.quick_sort(A,0,A.size());
for(auto &x:A){
see(x);
}
}
int main(){
test();
// test_cutoff(24);
return 0;
}


![[JAVA数据结构]希尔排序/缩小增量法](https://img-blog.csdnimg.cn/623ef95603cf411c91edb4467c00534d.png)