离散Markov Chain序列及可视化

---

文章目录

• 离散Markov Chain序列及可视化
• • @[toc]
  • 1 天气预测
  • 2 赌徒问题

1 天气预测

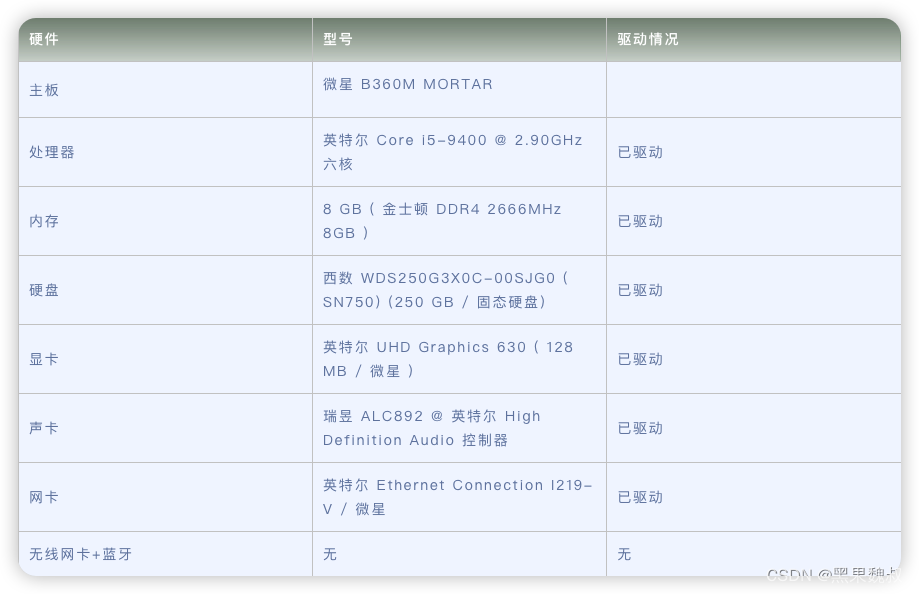
假设仅存在三种天气：晴天、阴天和雨天，每种天气状态构成的系统满足(齐次)马氏链过程，即下一期的天气状态仅取决于当前的天气状态，基于先验概率统计得到某地天气状态转移概率矩阵如下

     晴天 阴天 雨天
晴天  0.8 0.15 0.05
阴天  0.2 0.60 0.20
雨天  0.1 0.30 0.60

即当前如是晴天，则明天是晴天的概率为0.8，是阴天的概率为0.15，是雨天的概率为0.05；其他同理。随着时间推移，每种状态均存在，因此不存在吸收态。

接下来使用R构建markovchain对象，基于markovchain对象生产预测序列及可视化。首先构建markovchain对象，安装并导入markovchain包即可

statesNames=c("晴天","阴天","雨天")
mcA<-new("markovchain", states=statesNames, transitionMatrix=
           matrix(c(0.8,0.15,0.05,0.2,0.6,0.2,0.1,0.3,0.6), nrow=3,
                  byrow=TRUE, dimnames=list(statesNames, statesNames)))
plot(mcA,edge.arrow.size = 0.4,edge.color = 3,edge.width = 2,
     edge.curved = 0.1,vertex.shape = "rectangle")

计算不同天气状态平稳分布

steadyStates(mcA)
#           晴天      阴天      雨天
# [1,] 0.4444444 0.3333333 0.2222222

给定初始状态，基于上述天气马氏链生成未来100期的天气状态

markovchainSequence(n=100, markovchain=mcA, 
                    t0 = mcA@states[1],include=TRUE)
# [1] "晴天" "晴天" "晴天" "晴天" "晴天" "雨天" "雨天" "晴天" "晴天"
# [10] "阴天" "阴天" "阴天" "阴天" "雨天" "雨天" "阴天" "阴天" "阴天"
# [19] "阴天" "雨天" "雨天" "阴天" "晴天" "阴天" "雨天" "雨天" "晴天"
# [28] "晴天" "阴天" "晴天" "阴天" "阴天" "晴天" "晴天" "晴天" "晴天"
# [37] "晴天" "晴天" "阴天" "晴天" "晴天" "晴天" "晴天" "晴天" "晴天"
# [46] "晴天" "晴天" "晴天" "晴天" "晴天" "晴天" "晴天" "雨天" "雨天"
# [55] "晴天" "晴天" "晴天" "晴天" "晴天" "晴天" "晴天" "晴天" "晴天"
# [64] "晴天" "阴天" "阴天" "阴天" "阴天" "阴天" "阴天" "晴天" "晴天"
# [73] "晴天" "晴天" "晴天" "晴天" "晴天" "晴天" "阴天" "雨天" "阴天"
# [82] "阴天" "阴天" "阴天" "雨天" "阴天" "晴天" "晴天" "晴天" "晴天"
# [91] "阴天" "阴天" "阴天" "阴天" "阴天" "阴天" "阴天" "阴天" "阴天"
# [100] "雨天" "阴天"

反过来也可以根据一段时期内的天气序列估计天气马氏链转换概率矩阵，估计方法包括统计法，极大似然估计和bootstrap方法。

sequence = c("晴天", "晴天" ,"晴天", "晴天" ,"雨天", "阴天", "阴天", "阴天", "雨天"
             ,"雨天", "雨天" ,"阴天" ,"阴天" ,"阴天", "晴天", "晴天", "晴天", "雨天"
             ,"雨天" ,"雨天", "雨天", "雨天" ,"阴天", "晴天" ,"晴天" ,"阴天", "晴天"
             ,"晴天", "晴天" ,"阴天" ,"阴天" ,"阴天", "阴天", "阴天", "阴天", "晴天"
             ,"阴天", "阴天", "晴天" ,"晴天" ,"晴天", "晴天" ,"晴天", "阴天", "阴天"
             ,"阴天", "阴天", "阴天", "阴天" ,"雨天", "雨天" ,"雨天", "阴天", "阴天"
             ,"阴天", "阴天", "阴天", "阴天", "雨天", "晴天" ,"阴天" ,"雨天", "雨天"
             ,"雨天" ,"阴天" ,"晴天" ,"晴天" ,"雨天" ,"雨天" ,"雨天", "雨天" ,"阴天"
             ,"阴天" ,"阴天", "晴天" ,"阴天" ,"阴天", "阴天", "阴天" ,"雨天", "阴天"
             ,"阴天" ,"阴天" ,"雨天", "雨天" ,"雨天" ,"雨天" ,"阴天", "阴天", "阴天"
             ,"阴天" ,"阴天" ,"阴天", "晴天", "阴天" ,"阴天", "晴天" ,"阴天", "阴天"
             ,"阴天" ,"阴天")

基于计数的统计方法

sequenceMatr <- createSequenceMatrix(sequence, sanitize = FALSE)
sequenceMatr
#        晴天 阴天 雨天
# 晴天   13    8    3
# 阴天    9   36    6
# 雨天    1    8   16

基于极大似然估计方法

mcFitMLE <- markovchainFit(data = sequence)
mcFitMLE$estimate
#          晴天      阴天      雨天
# 晴天 0.5416667 0.3333333 0.1250000
# 阴天 0.1764706 0.7058824 0.1176471
# 雨天 0.0400000 0.3200000 0.6400000
mcFitMLE$standardError
#          晴天      阴天       雨天
# 晴天 0.15023130 0.1178511 0.07216878
# 阴天 0.05882353 0.1176471 0.04802921
# 雨天 0.04000000 0.1131371 0.16000000
# 还包括置信水平、置信区间不再演示

基于bootstrap方法

mcFitBSP <- markovchainFit(data = sequence, 
                           method = "bootstrap", 
                           nboot = 100, 
                           name = "Bootstrap Mc")

mcFitBSP$estimate 
#          晴天      阴天      雨天
# 晴天 0.50632697 0.3591076 0.1345655
# 阴天 0.17673460 0.6971927 0.1260727
# 雨天 0.04392222 0.3457910 0.6102868

mcFitBSP$standardError
#         晴天        阴天        雨天
# 晴天 0.011204577 0.011693831 0.007900094
# 阴天 0.005394905 0.006909293 0.004826192
# 雨天 0.004952809 0.011784305 0.012170454

---

2 赌徒问题

在一次赌徒中，赢得1元概率为0.4，输掉1元概率为0.6，赌徒退出条件为输光或财富达到N元。假设随机变量$X_n$表示$n$次赌博后的财富数量，于是转移概率可表示为
$$\{\begin{array}{l}p(i,i-1)=P(X_{n+1}=i-1|X_n=i)=0.6\\ p(i,i+1)=P(X_{n+1}=i+1|X_n=i)=0.4\\ p(0,0)=p(N,N)=1\end{array}$$
假设财富达到$N=5$元时退出赌博，则转移概率矩阵为

    0元 1元 2元 3元 4元 5元
0元 1.0 0.0 0.0 0.0 0.0 0.0
1元 0.6 0.0 0.4 0.0 0.0 0.0
2元 0.0 0.6 0.0 0.4 0.0 0.0
3元 0.0 0.0 0.6 0.0 0.4 0.0
4元 0.0 0.0 0.0 0.6 0.0 0.4
5元 0.0 0.0 0.0 0.0 0.0 1.0

下面构建markovchain对象

statesNames = c('0元','1元','2元','3元','4元','5元')
mat = matrix(c(1,0,0,0,0,0,
               0.6,0,0.4,0,0,0,
               0,0.6,0,0.4,0,0,
               0,0,0.6,0,0.4,0,
               0,0,0,0.6,0,0.4,
               0,0,0,0,0,1), byrow=TRUE, nrow=6,
             dimnames=list(statesNames, statesNames))
mcB<-new("markovchain", states=statesNames, 
         transitionMatrix= mat)
plot(mcB,edge.arrow.size = 0.4,edge.color = 3,edge.width = 2,
     edge.curved = 0.6,vertex.shape = "rectangle")

马氏链图可以看出存在吸收态0元、5元。使用R计算吸收态

absorbingStates(mcB)
# "0元" "5元"

计算平稳分布

steadyStates(mcB)
#        0元 1元 2元 3元 4元 5元
# [1,]   0   0   0   0   0   1
# [2,]   1   0   0   0   0   0

---

-END-

参考文献：

冯玲，方杰. 随机过程及其在金融中的应用[M].北京：中国人民大学出版社，2020.10