前言

斐波那契数列每次学都有不一样的体会，从最开始简单理解就是，一个找规律的游戏，就是更新数值，往后算就行了，但是，后来，用斐波那契数列理解递归算法，是一个很好的例子，由上向下计算，依次回溯，最后，没想到斐波那契数列还能和动态规划联系起来。当然，斐波那契数列也有很多的变式，青蛙跳台阶、兔子繁殖、将数字翻译成字符串等。只有将最基本的理解到位，后面的变式才能游刃有余的解决。

青蛙跳台阶

题目

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

最优解结构性质

画图分析

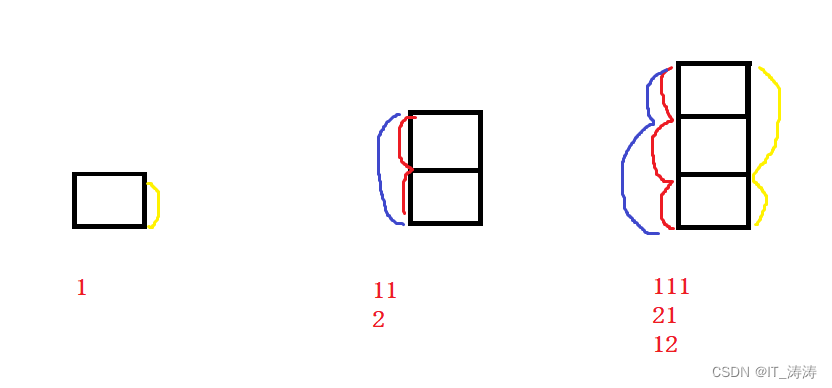
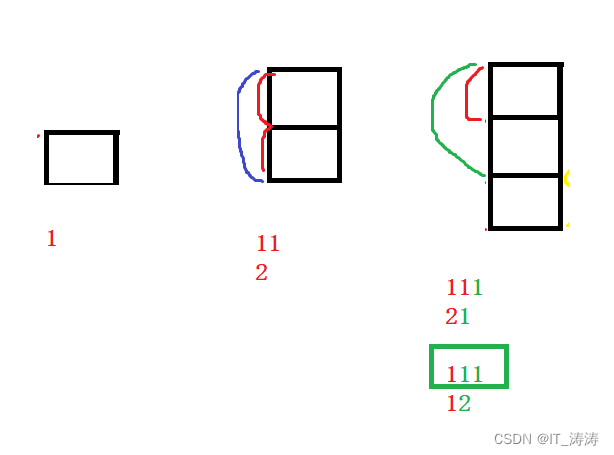
当只有1 2 3 节台阶的时候，我们可以直接画出来，比如2阶台阶时，有两种方法可以跳上去，每次跳1阶，跳两次，用11表示，或者直接跳2阶，用2表示
当有3阶台阶时有三种跳发，即 111 21 12
在这里插入图片描述

发现规律

对于3阶台阶，最后一步有两种跳发，跳一阶和两阶，
如果跳1阶，跳之前青蛙所处的位置在第2 阶台阶，只用跳一步就行，跳到第2阶台阶方法有11 2
在此基础上就是 111 21
如果跳2阶，跳之前青蛙所处的位置在第1阶台阶，要想跳到顶部，有两个办法，要么一步一步跳，即 111，要么直接跳两步即12 。即，111 12
可以看到，跳一阶和跳2阶，都有方法111 ，因为，在第1阶台阶时，你如果一步一步跳的话，你跳第一步的时候，你就变成了上一个情况(从第2阶台阶向上跳一步)，所以这里，不能跳一步，只能跳两步，即12
所以总的跳法就是 111 21 12
这种求法是建立在第1阶和第2阶基础上来的。

在这里插入图片描述

验证规律

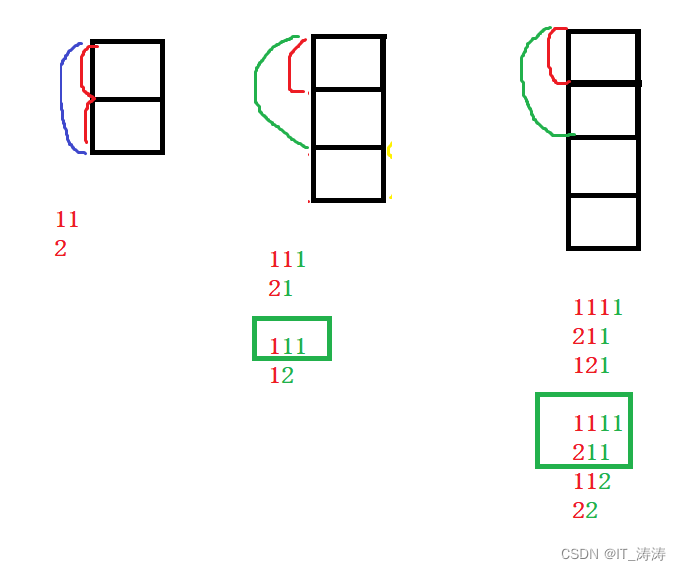
用1 2阶台阶推导第3阶的方法，根据2 3阶推导第4阶台阶。
到达第4阶台阶，要么从第3阶开始，就跳1步，要么从第2阶开始，跳2步，否则有重复
在这里插入图片描述

动规表达式

青蛙跳台阶

dp[i]表示到达第i阶台阶的跳法

dp[0]=1
dp[1]=1
dp[2]=2
dp[i]=dp[i-1]+dp[i-2]

与斐波那契数列的不同之处

可以先了解: 斐波那契数列的分析这样更好理解异同之处。
类似斐波那契数列，区别就是起始数字不同
斐波那契数列：0 1 1 2 3 5 …

dp[0]=0
dp[1]=1
dp[i]=dp[i-1]+dp[i-2]

递归实现

根据递归表达式，递归实现该算法

代码实现

#include<iostream>
#include<vector>
using namespace std;
int wayNums(int n) {
	if (n == 1|| n==0)return 1;
	return wayNums(n - 1) + wayNums(n - 2);
}
int main() {
	int num = wayNums(5);//8
	cout << num << endl;
	return 0;
}

测试结果

在这里插入图片描述

递归过程画图分析

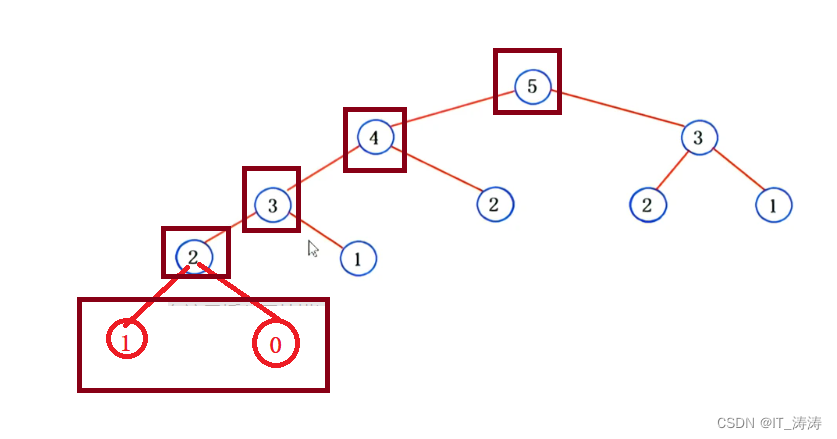
即你需要算跳到第5阶台阶的值，首先需要4 3 的值，以此类推，逐步回溯
在这里插入图片描述
递归算法，自顶而下，算了许多的重复值，即如图 wayNums(1)算了5次，wayNums(2)算了，3次，wayNums(3)算了2次。
我们用一个表记录重复的值，需要用的时候，我们在直接用，不用重新算了

非递归实现

根据已经有的值，自底而上，向上计算。

代码实现

#include<iostream>
#include<vector>
using namespace std;
int main() {
	vector<int>dp(6);
	dp[0] = 1;
	dp[1] = 1;
	for (int i = 2; i <= 5; i++) {
		dp[i] = dp[i - 1] + dp[i - 2];
	}
	cout << dp[5] << endl;
	return 0;
}