两个人有不想让第三者知道的事情,可以找一个私密的空间去聊。而互联网本身是一个开放的体系,双方在交换数据的时候会经历大量的第三者——公司的防火墙、ISP 的路由器,还有可能有黑客抓取数据。那么这个时候如果张三和李四有私密的话想聊,该怎么办呢?当然是加密传输,想办法让双发传输的数据只有双方才能理解。目前有两种主流的加密方式——对称加密和非对称加密
对称加密
最简单的加密算法
因此,在实际的操作中我们会使用更简单直接的方式计算加密,比如交换和取补操作就是很不错的选择。假设你要加密数字 1234,假设 x 的补是 10-x,那么取补就是得到 9876。单单看这个操作太容易被破解,这个时候我们将操作复杂化。假设有 3 种取补操作:
- 前两个数字取补,后两个不变得到:9834。记作 1 号方案;
后两个数字取补,前两个不变,得到:1276。记作 2 号方案;
全部取补,得到:9876,记作3 号方案。
然后我们再增加两种换序操作,以 1234 为例: - 相邻数字交换,得到 2143, 记作4 号方案;
- 数据对半交换,得到 3412,记作5 号方案。
这样,我们可以设计一个加密过程是这样的,取补和换序操作交替进行,一共进行 4 次。那么如果是 1-4-2-5 就代表一种加密顺序,以 1234 为例: - 前两个数字取补,得到 9834;
- 相邻数据交换,得到 8943;
- 后两个数字取补,得到 8967;
- 数据对半交换得到:6789。
于是 1234 被加密成了 6789。解密的时候,需要知道加密的顺序 1-4-2-5。那么解密的时候就逆着上述操作即可: - 数据对半交换得到:8967;
- 后两个数字取补:8943;
- 相邻数据交换:9834;
- 前两个数字取补:1234。
在上面的过程中,对 5 种加密方案的定义、以及约定进行 4 次交替取补、换序操作,我们称为“加密算法”。1-4-2-5 ,描述的是在过程中的具体方案,是密钥。
对称加密
加密方用 1-4-2-5 加密,解密方用相同的密钥解密——解密方知道加密过程是 1425 就可以解密。像这样,双方加密解密都用相同密钥的算法,我们称为对称加密算法。在实际的操作过程当中,因为都是针对二进制的操作,取补操作可以用异或操作来替代。另外,在其中的某些步骤还可以拿数据和密钥进行位计算,具体不同加密算法实现不同。
数据加密标准(DES)
数据加密标准(DES)算法在 1976 年被美国国家标准局定为使用标准,后来被广泛传播。目前已经被证明可以被暴力破解。所谓暴力破解,就是遍历所有可能的密钥解析数据的方法。举个例子,已知张三和李四传输的是中文,加密算法是 DES,那么拿出一小段数据进行暴力破解,尝试所有的密钥,如果能成功解析出中文词语(词语在词库中可以查到),那么说明破解成功。DES 采用的 56 位密钥,每次计算加密 64 位的数据。在实际的暴力破解过程中,比我上面描述的行为更加复杂。一个通用的暴力破解算法需要较大的算力,一些 DES 的破解算法需要239-241 次操作。这个数量级的操作,目前还没有超出人类计算能力的极限,如果显卡好一点,或者机器多一些还是可以承受的。因此后续很多组织开始利用 3 次 DES 操作来增加破解成本,具体的做法是用 3 个 56 位的密钥组合成一个 168 位的密钥,对数据进行 3 次 DES 操作,这样做大大增加了暴力破解的成本。但是目前针对 3DES 仍然有一些攻击策略,需要 290 次计算和 288 位内存,虽然有一定概率被攻破,但是成本非常高。
高级加密标准
为了应对暴力破解等问题,很多团队选择对称加密算法时开始使用高级加密标准(AES),这个加密法用 128 位密钥,并设计了更难破解的算法。具体我不展开了,如果你在项目中需要使用对称加密,你可以用这个算法。
对称加密的缺陷
使用对称加密双方都知道密钥和算法,会造成很多问题。你可以先这样思考:如果你是一个网站提供服务给用户,你和用户之间如果使用对称加密,那么你需要为每个用户定时生成一个不同的密钥。这是因为,如果所有用户都用一个密钥,那么理论上一个用户就可以看到其他用户和网站之间的通信。有同学会问:以现在的技术给不同的客户端生成一个密钥难道有什么难度吗? 比如一个 UV 在 1000W 的网站,如果每天需要给每个用户生成一次密钥也就是 1000W 次计算,按照现在集群的能力,别说一天,每秒做到生成1000W 个密钥又有什么难度呢?因此,我们还需要进一步思考对称加密的问题。进一步的思考:对称加密安全吗?如果客户端不慎遗失密钥,让黑客拿到后果是什么?后果是黑客可以轻易伪装成服务端和客户端进行通信。在对称加密中,加密解密用的一个密钥,加密是正向过程,解密是逆向过程。那么有没有更好的方案呢?
非对称加密
为了进一步提升安全系数,数学家还提出了非对称加密。在非对称加密中,加密和解密用的不是一个密钥。类比生活中的场景,如果一个礼物箱子,开锁和上锁用的是不同的钥匙会发生什么?只拥有上锁钥匙的人,可以把礼物放到箱子里,但是他只有一次机会,也就是一旦他将礼物上锁,即便反悔了也没法再打开箱子。而收礼物的人只能开箱子取走礼物。如果放礼物的人丢了钥匙,箱子也不会被中间人打开。这个例子类比网络传输的世界,可以防止数据被监听、盗用、篡改……当我们开发一个网站,我们的用户之间的通信用非对称加密。用户发送请求时,用户用一把钥匙加密数据,网站用另一把钥匙解密。在这个过程中,网站拥有的钥匙称为私钥,用户拥有的钥匙称为公钥。之所以这样称呼,是因为很多用户可以共用一把公钥,而只有网站才拥有私钥。
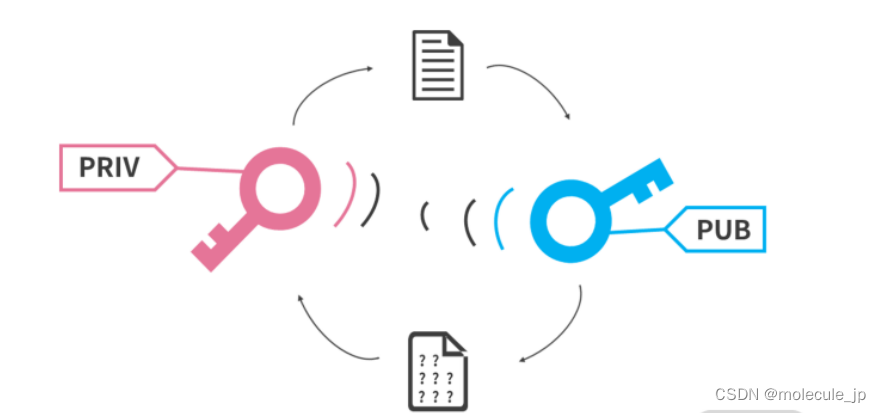
公钥发送的数据必须用私钥解密, 私钥发送的数据必须用公钥解密。网站发送数据加密用私钥,用户用公钥解密。用户发送数据用公钥,网站用私钥解密。而如果用户公钥不小心被盗,黑客也无法通过这把钥匙看其他用户的数据,因为黑客拿不到私钥。另外,当一个数据用公钥加密后,黑客也不可能查阅、篡改数据,因为黑客拿不到私钥。如果黑客要拿到私钥会怎么做呢?比如雇佣特工潜入物理机房、在该网站员工的机器上植入木马,买通公司内部员工购买等——世界上当然没有攻不破的秘密,只要花足够的代价。我们做信息安全,就是要尽量提升黑客的代价。
密钥的创建
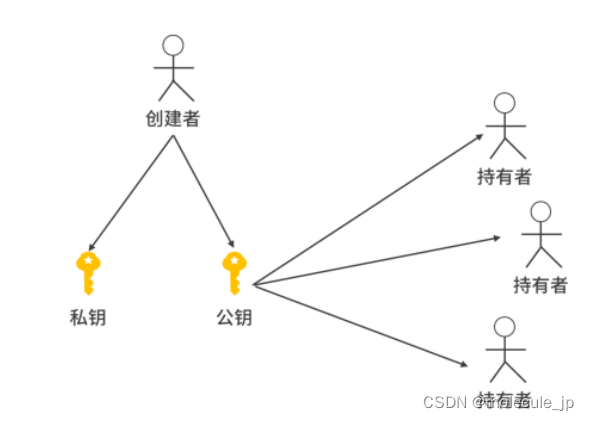
在非对称加密中,密钥通常由提供服务的一方创建。每次创建是一对公私钥对,然后提供者将公钥给用户,自己保留私钥。值得一提的是,我们在 Linux 环境可以用 openssl 创建公私钥对。
下面这行语句就可以生成一个私钥文件:
openssl genrsa -des3 -out privkey.pem 2048
接下来我们可以基于私钥生成公钥:
openssl rsa -in privkey.pem -inform pem -pubout -out pubkey.pem
常见非对称加密算法
目前最常见且广泛使用的非对称加密算法是 RSA 算法。RSA 依赖的是大整数的分解,以及一些和素数相关的算法。目前没有理论可以破译 RSA 算法。总体来说,RSA 密钥越长破解成本就越高,因此仍然被广泛使用。其他的非对称加密算法还有 DSS、EIGamal 等。
常见的应用场景
非对称加密算法目前广泛应用到各个领域,比如 HTTPS 协议的握手和交换密钥过程需要非对称加密算法;SSH 的通信需要非对称加密算法。另外,证书的生程,比如利用证书实现 git 账号的免密操作也是基于非对称加密算法。在线合同、数字货币的签名等都需要非对称加密算法。
总结
对称加密用同样的密钥,安全系数不够。非对称加密,用公钥 + 私钥的方式加强了安全系数。那么是不是我们所有的加密的应用都应该用非对称加密呢?通常情况,非对称加密需要更多的运算资源。因此很多协议使用非对称加密解决最核心的安全问题,再用对称加密解决其他问题。以 HTTPS 协议为例,客户端和服务器之间会先用非对称加密交换临时对称加密密钥,然后之后的通信会以对称加密执行,直到连接结束。也就是非对称加密仅仅存在于 HTTPS 连接建立后,用于交换密钥(对称加密密钥)的少数几次传输中。这样用非对称加密解决最核心的安全问题:交换对称加密密钥;然后利用对称加密进行数据的传输。
对称加密和解密可以用同一套密钥。非对称加密利用数学的方法生成公私钥对,公钥加密的数据私钥可以解密,私钥加密的数据公钥可以解密。但是公钥不能解密公钥加密的数据,私钥也不能解密私钥加密的数据。