第1关:树和二叉树基本概念
任务描述
本关任务:根据所学树和二叉树的基本概念等相关知识,完成右侧的选择题。
相关知识
树的定义
从数据结构角度看,树包含n(n≥0)个结点,当n=0时,称为空树;非空树的定义如下:
T=(D,R) 其中,D为树中结点的有限集合,关系R满足以下条件:
- 有且仅有一个结点d0∈D,它对于关系R来说没有前驱结点,结点d0称作树的根结点。
- 除根结点d0外,D中的每个结点有且仅有一个前驱结点,但可以有多个后继结点。
- D中可以有多个终端结点。
【例】 有一棵树T=(D,R),其中 D={A,B,C,D,E,F,G,H}, R={r} r={<A,B>,<A,C>,<A,D>,<C,E>,<C,F>,<D,G>,<E,H>} 画出其逻辑结构图。
解:A是根结点,其余结点分成三个互不相交的子集: T1={B},T2={C,E,F,H},T3={D,G}。 T1、T2、T3都是根结点A的子树,且各自本身也是一棵树。
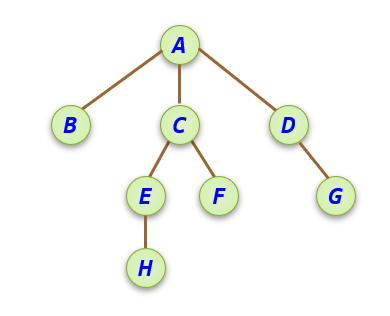
说明:树中结点之间的关系应为有向关系,在上图中,结点之间的连线即分支线都是有向的,默认箭头向下的。
树的基本术语
**结点的度:**树中每个结点具有的子树数或者后继结点数称为该结点的度。

树的度: 树中所有结点的度的最大值称之为树的度。 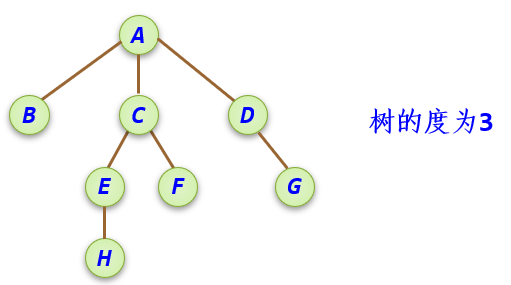
分支结点: 度大于0的结点称为分支结点或非终端结点。度为1的结点称为单分支结点,度为2的结点称为双分支结点,依次类推。 
叶子结点(或叶结点): 度为零的结点称为叶子结点或终端结点。 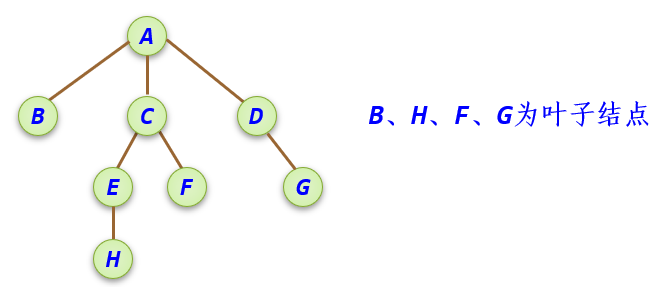
孩子结点: 一个结点的后继称之为该结点的孩子结点。 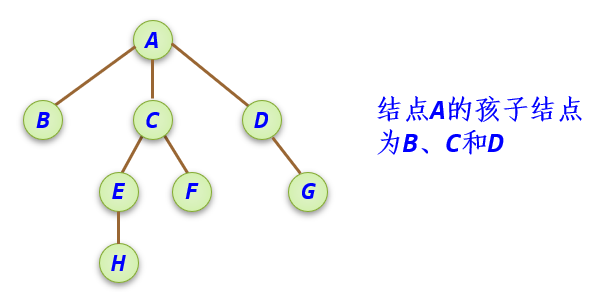
双亲结点(或父亲结点): 一个结点称为其后继结点的双亲结点。 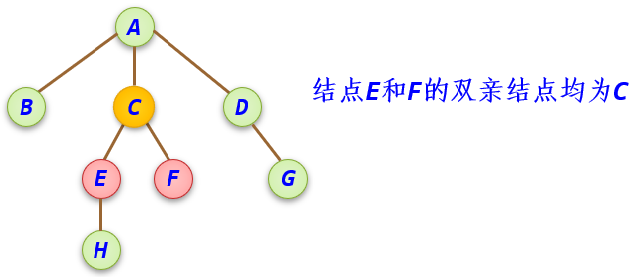
子孙结点: 一个结点的子树中除该结点外的所有结点称之为该结点的子孙结点。 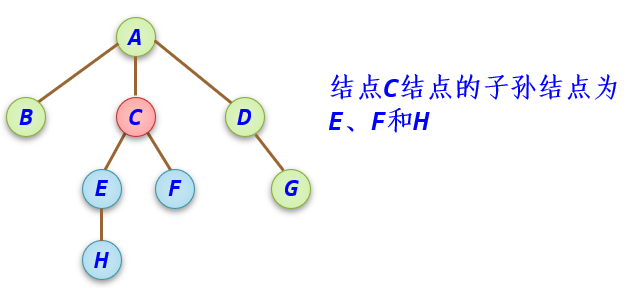
祖先结点: 从树根结点到达某个结点的路径上通过的所有结点称为该结点的祖先结点(不含该结点自身)。 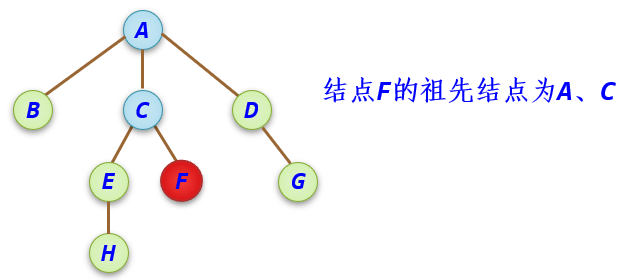
兄弟结点: 具有同一双亲的结点互相称之为兄弟结点。 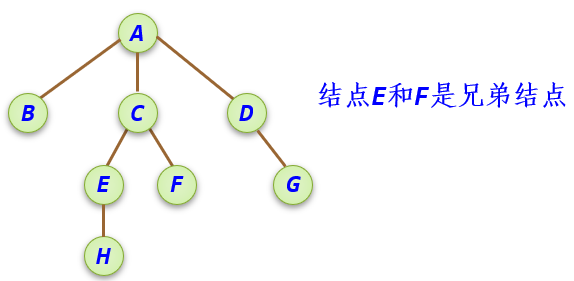
结点层次: 树具有一种层次结构,根结点为第一层,其孩子结点为第二层,如此类推得到每个结点的层次。 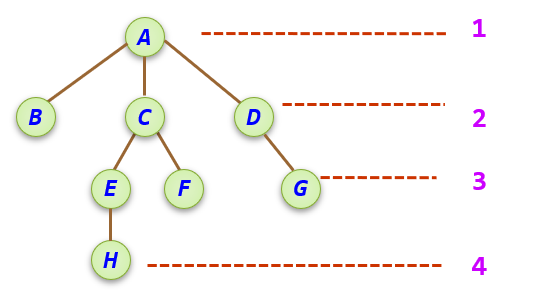
树的高度: 树中结点的最大层次称为树的高度或深度。 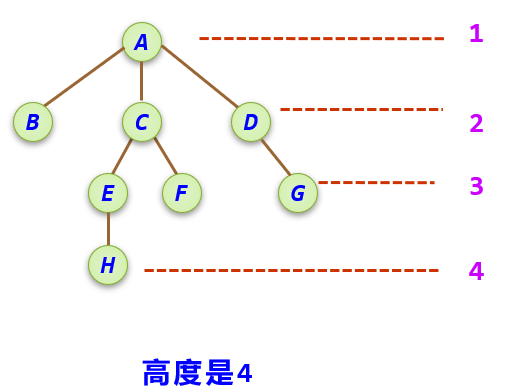
森林: 零棵或多棵互不相交的树的集合称为森林。 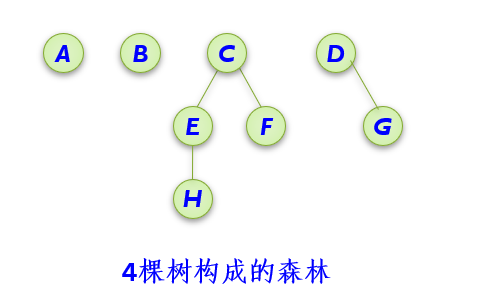
树的运算
树的运算主要分为三大类:
- 查找满足某种特定关系的结点,如寻找当前结点的双亲结点等;
- 插入或删除某个结点,如在树的当前结点上插入一个新结点或删除当前结点的第i个孩子结点等;
- 遍历树中每个结点。
二叉树的定义
二叉树的递归定义:
- 二叉树或者是一棵空树。
- 或者是一棵由一个根结点和两棵互不相交的分别称做根结点的左子树和右子树所组成的非空树,左子树和右子树又同样都是一棵二叉树。
二叉树与度为2的树的区别:
- 度为2的树至少有3个结点,而二叉树的结点数可以为0。
- 度为2的树不区分子树的次序,而二叉树中的每个结点最多有两个孩子结点,且必须要区分左右子树,即使在结点只有一棵子树的情况下也要明确指出该子树是左子树还是右子树。
二叉树的5种形态: 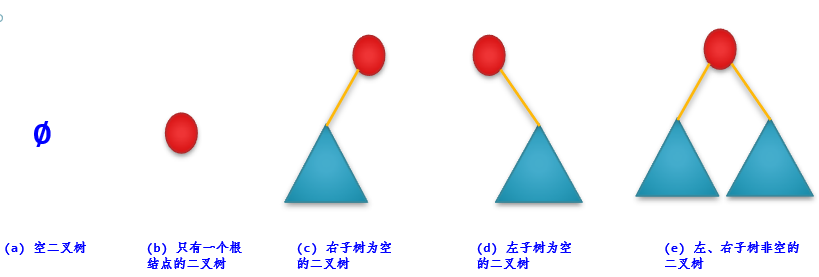
二叉树的性质
性质1 非空二叉树上叶结点数等于双分支结点数加1。即n0=n2+1。 约定:二叉树上叶结点数为n0,单分支结点数为n1,双分支结点数为n2,
性质2 非空二叉树上第i层上至多有 2i−1 个结点,这里应有i≥1。
性质3 高度为h的二叉树至多有2h−1个结点(h≥1)。
满二叉树:在一棵二叉树中,当第i层的结点数为2i−1个时,则称此层的结点数是满的,当一棵二叉树中的每一层都满时,且叶子结点在同一层上,则称此树为满二叉树。
满二叉树特性:
- 除叶子结点以外的其他结点的度皆为2。
- 高度为h的满二叉树中的结点数为
2h−1个。 - 层序编号:从根结点为1开始,按照层次从小到大、同一层从左到右的次序顺序编号。可以对满二叉树的结点进行连续编号。
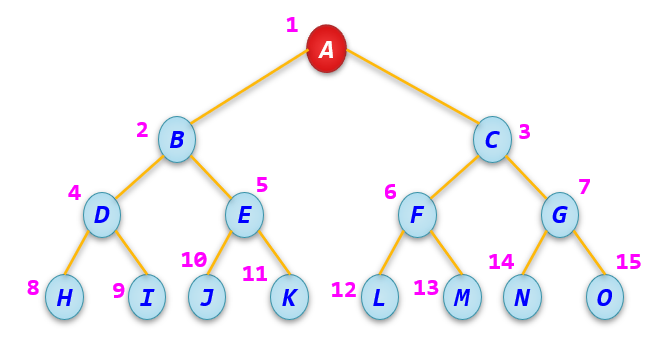
完全二叉树:在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干个结点,则称此树为完全二叉树。
完全二叉树特性:
- 完全二叉树中至多只有最下边两层结点的度数小于2。
- 高度为h的完全二叉树若按层序编号,它与高度为h的满二叉树中结点的编号一一对应。
如下图所示的一棵完全二叉树,它与等高度的满二叉树相比,在最后一层的右边缺少了3个结点。
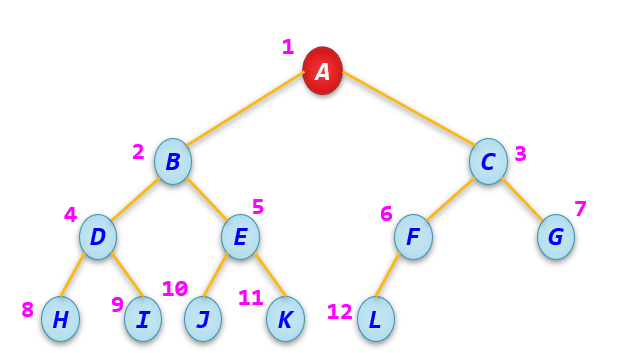
性质4 对完全二叉树中编号为i的结点(1≤i≤n,n≥1,n为结点数)有: (1)若 i⩽└2n┘,即2i≤n,则编号为i的结点为分支结点,否则为叶子结点。 (2)若n为奇数,则每个分支结点都既有左孩子结点,也有右孩子结点; 若n为偶数,则编号最大的分支结点只有左孩子结点,没有右孩子结点,其余分支结点都有左、右孩子结点。 (3)若编号为i的结点有左孩子结点,则左孩子结点的编号为2i;若编号为i的结点有右孩子结点,则右孩子结点的编号为(2i+1)。 (4)除树根结点外,若一个结点的编号为i,则它的双亲结点的编号为 └2i┘,也就是说,当i为偶数时,其双亲结点的编号为2i,它是双亲结点的左孩子结点,当i为奇数时,其双亲结点的编号为2i−1,它是双亲结点的右孩子结点。 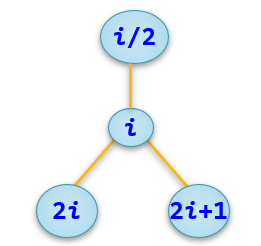
编程要求
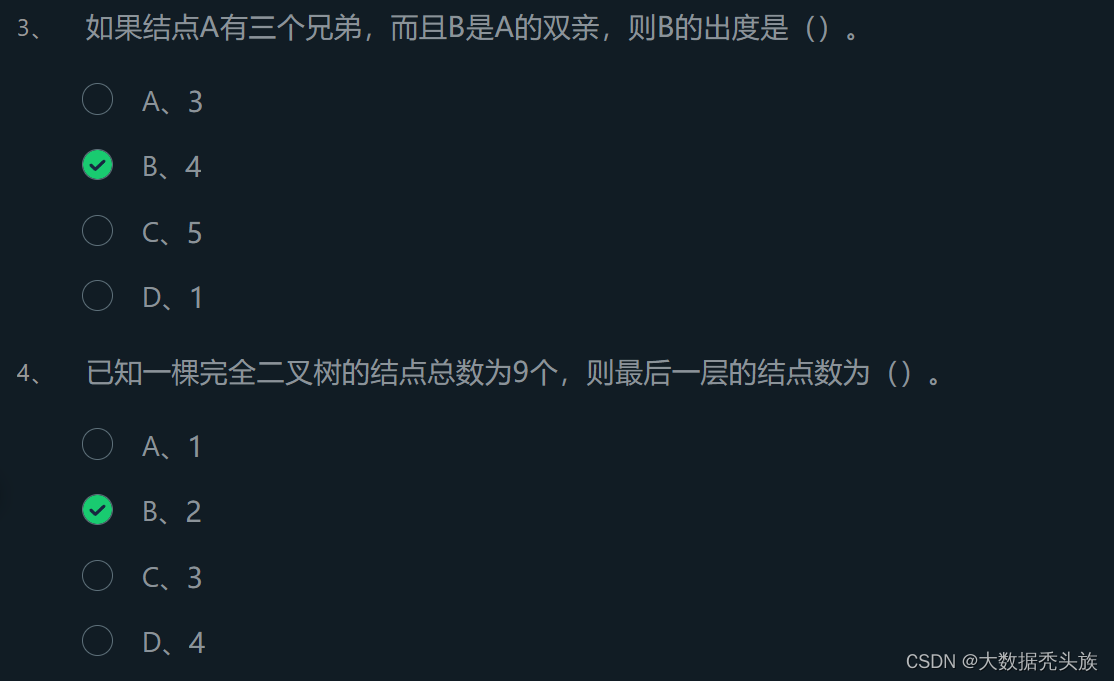
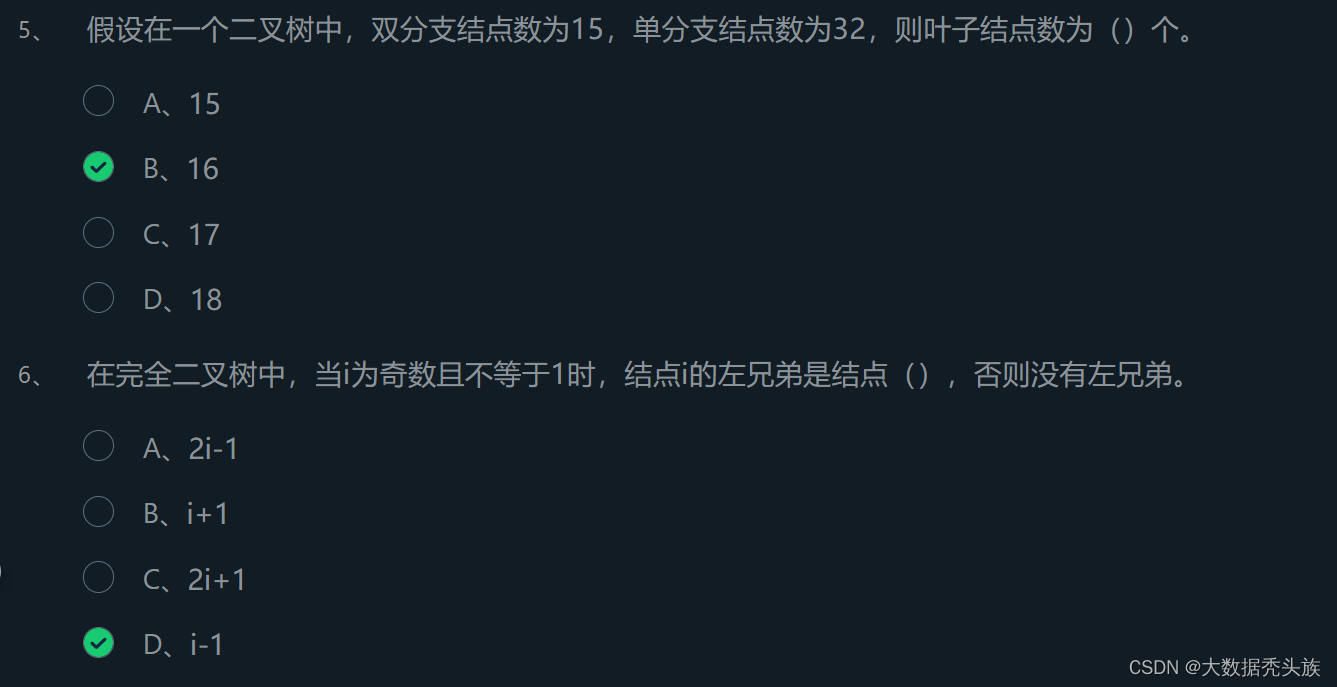
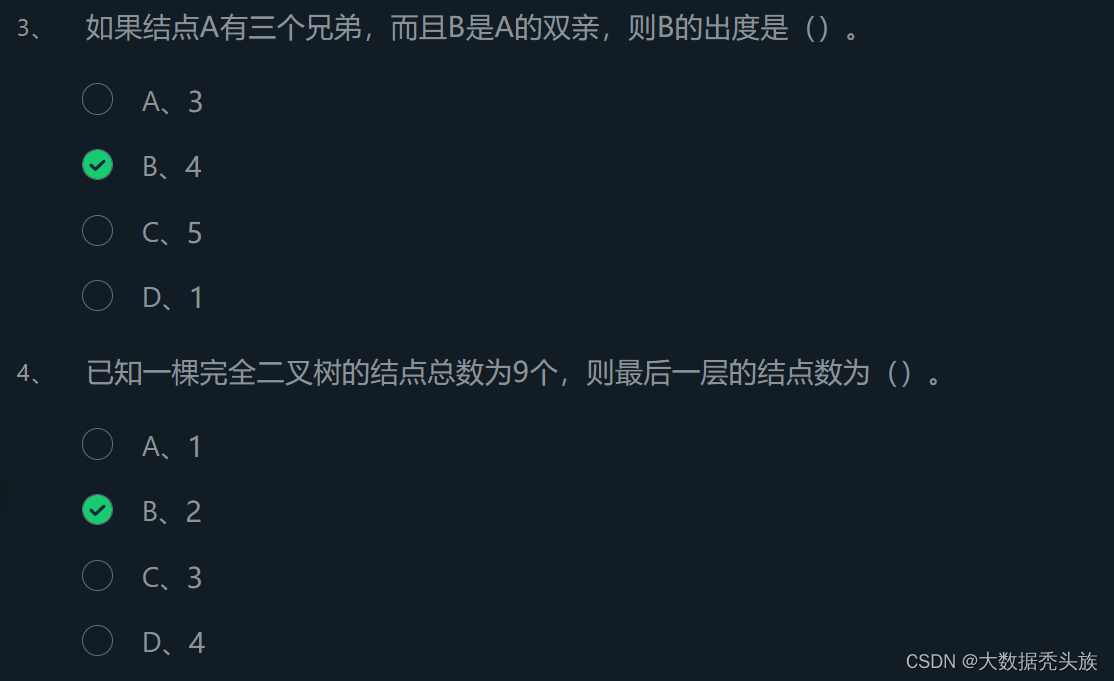
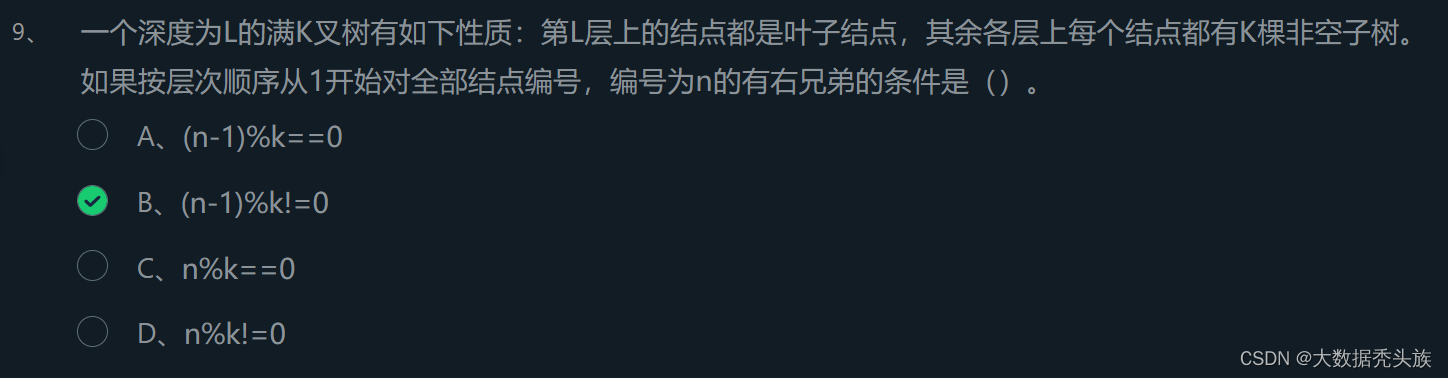
根据提示,完成单选题。
开始你的任务吧,祝你成功!
实例

第2关:二叉树的顺序存储及基本操作
任务描述
本关任务:以顺序结构存储二叉树,编写前序、中序、后序及层次顺序遍历二叉树的算法,并计算二叉树深度、所有结点总数。
相关知识
二叉树的定义
二叉树的递归定义:
- 二叉树或者是一棵空树。
- 或者是一棵由一个根结点和两棵互不相交的分别称做根结点的左子树和右子树所组成的非空树,左子树和右子树又同样都是一棵二叉树。

二叉树与度为2的树的区别:
- 度为2的树至少有3个结点,而二叉树的结点数可以为0。
- 度为2的树不区分子树的次序,而二叉树中的每个结点最多有两个孩子结点,且必须要区分左右子树,即使在结点只有一棵子树的情况下也要明确指出该子树是左子树还是右子树。
二叉树的5种形态: 
二叉树的性质
性质1 非空二叉树上叶结点数等于双分支结点数加1。即n0=n2+1。 约定:二叉树上叶结点数为n0,单分支结点数为n1,双分支结点数为n2,
性质2 非空二叉树上第i层上至多有 2i−1 个结点,这里应有i≥1。
性质3 高度为h的二叉树至多有2h−1个结点(h≥1)。
满二叉树:在一棵二叉树中,当第i层的结点数为2i−1个时,则称此层的结点数是满的,当一棵二叉树中的每一层都满时,且叶子结点在同一层上,则称此树为满二叉树。
满二叉树特性:
- 除叶子结点以外的其他结点的度皆为2。
- 高度为h的满二叉树中的结点数为
2h−1个。 - 层序编号:从根结点为1开始,按照层次从小到大、同一层从左到右的次序顺序编号。可以对满二叉树的结点进行连续编号。

完全二叉树:在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干个结点,则称此树为完全二叉树。
完全二叉树特性:
- 完全二叉树中至多只有最下边两层结点的度数小于2。
- 高度为h的完全二叉树若按层序编号,它与高度为h的满二叉树中结点的编号一一对应。
如下图所示的一棵完全二叉树,它与等高度的满二叉树相比,在最后一层的右边缺少了3个结点。



二叉树的遍历
二叉树的遍历是指按一定的次序访问树中的所有结点,使每个结点恰好被访问一次。其中遍历次序保证了二叉树上每个结点均被访问一次且仅有一次。
二叉树常用的遍历有先序(根)遍历、中序(根)遍历、后序(根)遍历和层次遍历。
所谓先序、中序、后序,区别在于访问根结点的顺序。 1.先序遍历 若二叉树非空,则: ① 访问根结点; ② 先序遍历左子树; ③ 先序遍历右子树。 先序遍历序列的特点:其第一个元素值为二叉树中根结点值。
2.中序遍历 若二叉树非空,则: ① 中序遍历左子树; ② 访问根结点; ③ 中序遍历右子树。 中序遍历序列的特点:若已知二叉树的根结点值,以该值为界,将中序遍历序列分为两部分,前半部分为左子树的中序遍历序列,后半部分为右子树的中序遍历序列。
3.后序遍历 若二叉树非空,则: ① 后序遍历左子树; ② 后序遍历右子树; ③ 访问根结点。 后序遍历序列的特点:最后一个元素值为二叉树中根结点值。
4.层次遍历 层次遍历是从根结点出发,按照从上向下,同一层从左向右的次序访问所有的结点。采用层次遍历得到的访问结点序列称为层次遍历序列。 层次遍历序列的特点:其第一个元素值为二叉树中根结点值。
例:图1表示一个二叉树 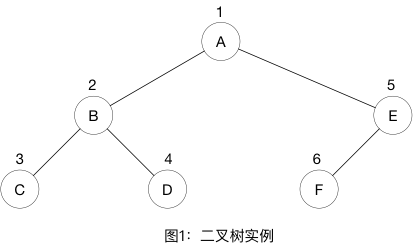
前序遍历:ABCDEF 中序遍历:CBDAFE 后序遍历:CDBFEA 层次遍历:ABECDF
二叉树也可以采用两种存储方式:顺序存储结构和链式存储结构。
二叉树的顺序存储结构
顺序存储一棵二叉树时,就是用一组连续的存储单元存放二叉树中的结点。
由二叉树的性质4可知,对于完全二叉树(或满二叉树),树中结点层序编号可以唯一地反映出结点之间的逻辑关系,所以可以用一维数组按从上到下、从左到右的顺序存储树中所有结点值,通过数组元素的下标关系反映完全二叉树或满二叉树中结点之间的逻辑关系。
一棵完全二叉树的顺序存储结构:
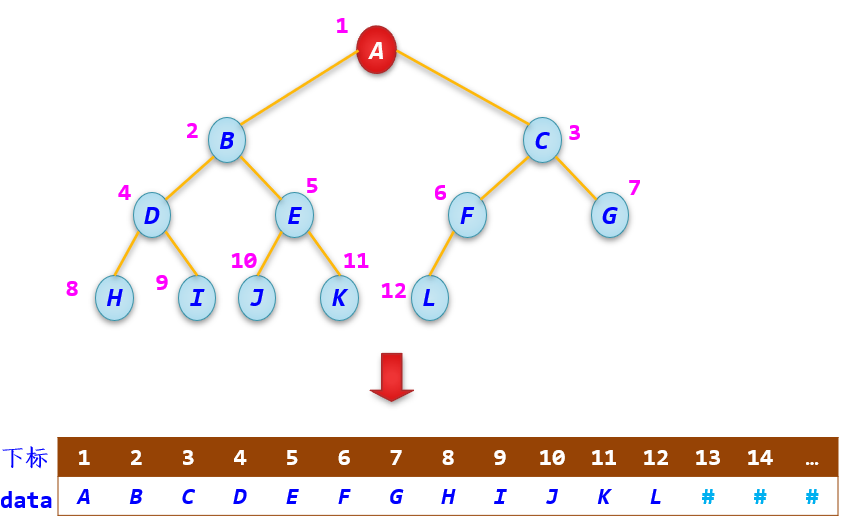
一般的二叉树的顺序存储结构:
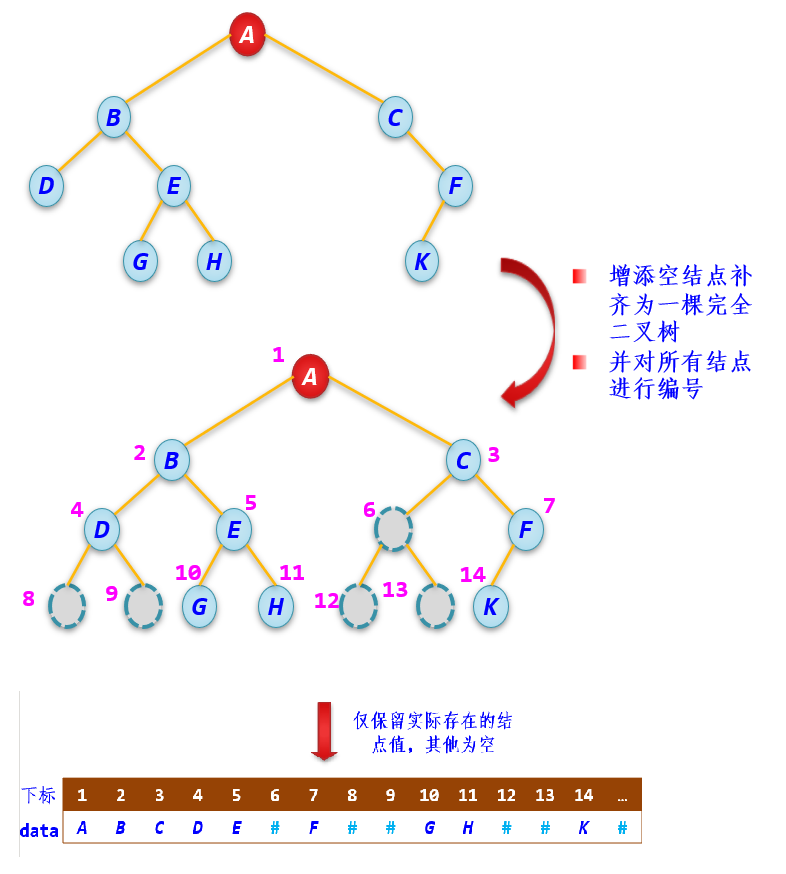
二叉树顺序存储结构的类型定义如下: typedef ElemType SqBinTree[MaxSize];
其中,ElemType为二叉树中结点的数据值类型,MaxSize为顺序表的最大长度。为了方便运算,通常将下标为0的位置空着,值为#的结点为空结点。
完全二叉树或满二叉树采用顺序存储结构比较合适,既能够最大可能地节省存储空间,又可以利用数组元素的下标确定结点在二叉树中的位置以及结点之间的关系。
对于一般二叉树,如果它接近于完全二叉树形态,需要增加的空结点个数不多,也可适合采用顺序存储结构。
如果需要增加很多空结点才能将一棵二叉树改造成为一棵完全二叉树,采用顺序存储结构会造成空间的大量浪费,这时不宜用顺序存储结构。例如:
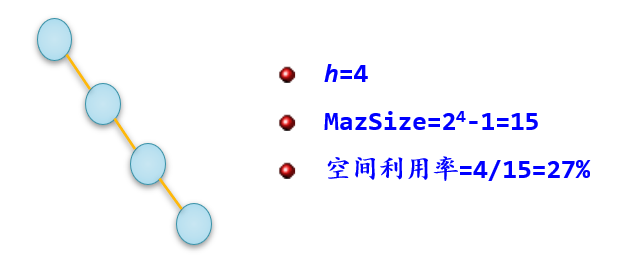
编程要求
根据提示,在右侧编辑器补充代码。具体要求如下:
InitBiTree(SqBiTree &T)//构造空二叉树T。CreateBiTree(SqBiTree &T)//按层序次序输入二叉树中结点的值(字符型或整型), 构造顺序存储的二叉树TBiTreeEmpty(SqBiTree T)//判断二叉树T是否为空二叉树,若是则返回TRUE,否则FALSEBiTreeDepth(SqBiTree T)//返回二叉树T的深度PreOrderTraverse(SqBiTree T,void(*Visit)(TElemType))//先序遍历二叉树T,对每个结点调用函数Visit一次且仅一次InOrderTraverse(SqBiTree T,void(*Visit)(TElemType))//中序遍历二叉树T,对每个结点调用函数Visit一次且仅一次PostOrderTraverse(SqBiTree T,void(*Visit)(TElemType))//后序遍历二叉树T,对每个结点调用函数Visit一次且仅一次LevelOrderTraverse(SqBiTree T,void(*Visit)(TElemType))// 层序遍历二叉树
测试说明
平台会对你编写的代码进行测试:
测试输入:ABCDEF###G##H
预期输出:
按先序遍历的结果为:ABDEGCFH
按中序遍历的结果为:DBGEAFHC
按后序遍历的结果为:DGEBHFCA
按层序遍历的遍历结果为:ABCDEFGH
该二叉树的高度为:4
开始你的任务吧,祝你成功!
实例
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#define OK 1
#define ERROR 0
#define MAX_TREE_SIZE 100
typedef char TElemType ;
typedef TElemType SqBiTree[MAX_TREE_SIZE];
TElemType Nil='#';
void input(TElemType &x) // 函数变量
{
scanf("%c",&x);
}
void visit(TElemType x) // 函数变量
{
printf("%c",x);
}
void InitBiTree(SqBiTree &T)
{ // 构造空二叉树T。因为T是数组名,故不需要&
int i;
for(i=0;i<MAX_TREE_SIZE;i++)
T[i]=Nil; // 初值为空(Nil在主程中定义)
}
void CreateBiTree(SqBiTree &T)
{ // 按层序次序输入二叉树中结点的值(字符型或整型), 构造顺序存储的二叉树T
/********** Begin **********/
int i=1;
scanf("%s",T+1);
while(T[i] != '\0')
i++;
T[i]='#';
/********** End **********/
}
int BiTreeEmpty(SqBiTree T)
{ // 初始条件:二叉树T存在。操作结果:若T为空二叉树,则返回TRUE,否则FALSE
if(T[1]==Nil) // 根结点为空,则树空
return 1;
else
return 0;
}
int BiTreeDepth(SqBiTree T)
{ // 初始条件:二叉树T存在。操作结果:返回T的深度
/********** Begin **********/
int i=MAX_TREE_SIZE-1,j;
while(T[i]=='#')
i--;
j=i;
int dep=0;
do
{
dep++;
j=j/2;
}while(j>=1);
return dep;
/********** End **********/
}
void PreTraverse(SqBiTree T,int e)
{ // PreOrderTraverse()调用
/********** Begin **********/
if(T[e] != '#')
{
visit(T[e]);
PreTraverse(T,2*e);
PreTraverse(T,2*e+1);
}
/********** End **********/
}
void PreOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 初始条件:二叉树存在,Visit是对结点操作的应用函数
// 操作结果:先序遍历T,对每个结点调用函数Visit一次且仅一次
if(!BiTreeEmpty(T)) // 树不空
PreTraverse(T,1);
printf("\n");
}
void InTraverse(SqBiTree T,int e)
{ // InOrderTraverse()调用
/********** Begin **********/
if(T[e] != '#')
{
InTraverse(T,2*e);
visit(T[e]);
InTraverse(T,2*e+1);
}
/********** End **********/
}
void InOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 初始条件:二叉树存在,Visit是对结点操作的应用函数
// 操作结果:中序遍历T,对每个结点调用函数Visit一次且仅一次
if(!BiTreeEmpty(T)) // 树不空
InTraverse(T,1);
printf("\n");
}
void PostTraverse(SqBiTree T,int e)
{ // PostOrderTraverse()调用
/********** Begin **********/
if(T[e] != '#')
{
PostTraverse(T,2*e);
PostTraverse(T,2*e+1);
visit(T[e]);
}
/********** End **********/
}
void PostOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 初始条件:二叉树T存在,Visit是对结点操作的应用函数
// 操作结果:后序遍历T,对每个结点调用函数Visit一次且仅一次
if(!BiTreeEmpty(T)) // 树不空
PostTraverse(T,1);
printf("\n");
}
void LevelOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 层序遍历二叉树
/********** Begin **********/
int dep=BiTreeDepth(T);
int tree_max=pow(dep,2)-1;
for(int i=1;i<tree_max;i++){
if(T[i]=='#')
continue;
visit(T[i]);
}
printf("\n");
/********** End **********/
}
int main()
{
TElemType e;
SqBiTree Bt,s;
InitBiTree(Bt);
CreateBiTree(Bt);
printf("按先序遍历的结果为:");
PreOrderTraverse(Bt,visit);
printf("按中序遍历的结果为:");
InOrderTraverse(Bt,visit);
printf("按后序遍历的结果为:");
PostOrderTraverse(Bt,visit);
printf("按层序遍历的遍历结果为:");
LevelOrderTraverse(Bt,visit);
printf("该二叉树的高度为:%d\n",BiTreeDepth(Bt) );
return 0;
}