并查集用于计算图连通分量。
比如回答这样的问题:
- 社交媒体中,用户A和用户B是否属于同一个圈子里的?
- 一个城市到另一个城市是否是可达的?
并查集适用于并不需要计算出图上具体的路径,只需要计算是否连通。
public interface UnionFindSet {
// 节点a 和 节点b 是否连通,可达
public boolean isConnect(int a, int b);
// 合并节点a和节点b所属群
public int union(int a,int b);
}
什么是并查集
为了方便理解,数形结合一下:
通常使用数组来标记所有节点所属的群组,如下图所示,parent[i]代表第i个节点的父亲。
初始状态下,每个节点的父亲节点都是自己,代表自己单独一个组:
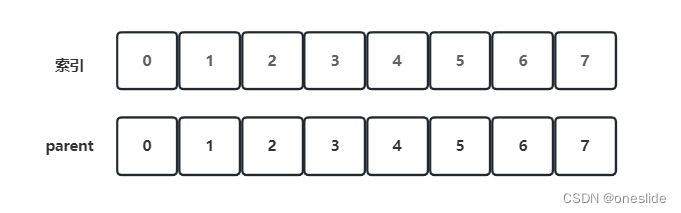
分别将1,2,4合并,6,7合并:
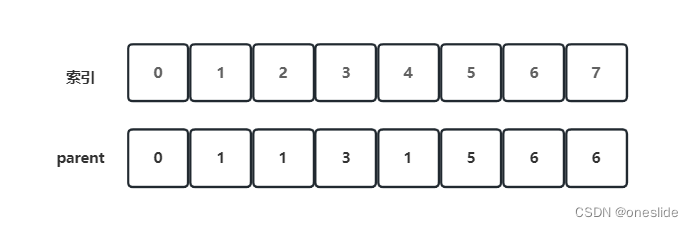
此时,多了2个大小超过1的树。parent[i] = 1代表属于节点1为祖先的群组。判断两个节点是否属于同一群组,只需要判断父亲是否相同即可。
如何合并两个节点呢? 下面给出一个简单实现:
遍历更新
遍历更新的方式,即遍历parent数组将所有属于群组b的节点的父亲设置为群组a的父亲.
public class UnionFind {
private final int[] parent;
public UnionFind(int size){
parent= new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
public boolean isConnected(int a, int b){
return parent[a] == parent[b];
}
// 遍历`parent`数组将所有属于群组b的节点的父亲设置为群组a的父亲.
public int union(int a, int b){
if (parent[a] == parent[b]){
return parent[a];
}
for (int i = 0; i < parent.length; i++) {
if (parent[i] == parent[b]){
parent[i] = parent[a];
}
}
return parent[a];
}
}
这种方式优点是isConnected非常简单,因为树的深度只有一层,只需要一次引用即可。
但是有一个缺陷,即每次合并都要遍历一遍parent数组,其时间复杂度是O(n).
那么为了优化union操作的性能,可以将父子关系设置成一颗树,树可以很好的优化查询性能,合并时只需要将树根指向另一个树根即可。
使用树优化union操作
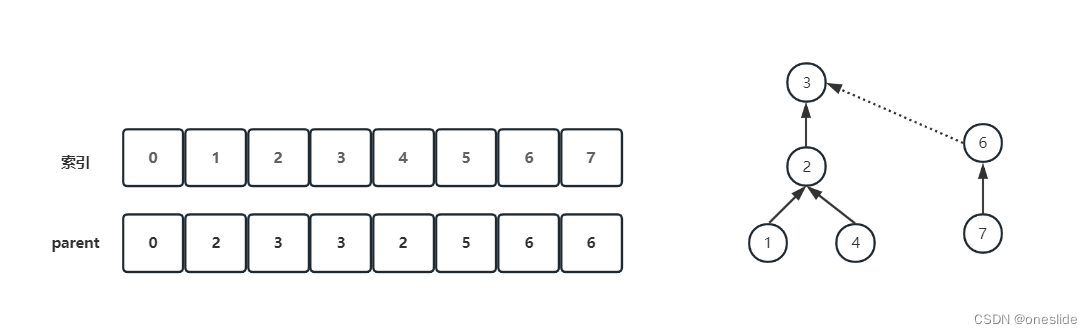
上面这棵树,1,2,3,4属于同一群组,6,7属于同一群组。如果将两个群组合并,只需要将节点6的父亲指向节点3.
因为现在群组关系里,树的深度不再为2,因此需要不断向上回溯,找到树根,复杂度为O(h). h为树高。
回溯操作使用一个新函数find来表示。
isConnected操作的复杂度为O(h).union操作的复杂度为O(h)
这个实现牺牲了较小的查询性能,换取union操作较大的性能提升。
但是还会出现一个问题,就是二叉树经常出现的不平衡问题。极端情况下,树会变成一个链表,其复杂度还会降低为O(n)。
那么为了解决这个问题,我们可以压缩路径,即减小树高。
public class UnionFind {
private final int[] parent;
public UnionFind(int size){
parent= new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
// 找到树根
public int find(int a){
if (parent[a]!=a){
a = parent[a];
}
return a;
}
public boolean isConnected(int a, int b){
return find(a) == find(b);
}
public int union(int a, int b){
int ap = find(a);
int bp = find(b);
if (ap == bp){
return ap;
}
parent[bp] = ap; // 直接将群组b的树根父亲设置为群组a的树根。
return ap;
}
}
路径压缩
路径压缩的方式有很多种,下面给出一种实现:
在find操作的过程中,将所有属于同一群组的节点的父亲,置为树根节点。很方便的使用递归来实现。
public class UnionFind {
// 记录节点的父亲节点
private final int[] parent;
public UnionFind(int size){
parent= new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
// 找到节点的祖先节点
public int find(int a){
if (parent[a]!= a){
parent[a] = find(parent[a]); // 将a节点的父亲直接设置成祖先,压缩路径
}
return parent[a]; // 递归结束条件为parent[a]== a,即自己是自己的父亲
}
// 祖先节点相同的节点属于同一群组
public boolean isConnected(int a, int b){
return find(a) == find(b);
}
// 合并两个节点所属群组
public int union(int a, int b){
int ap = find(a);
int bp = find(b);
// 属于同一群组则返回
if (ap == bp){
return ap;
}
// 属于不同群组,则将一个祖先的父亲置为另一个
parent[ap] = bp;
return ap;
}
}