前言:
属实是失踪人口回归了。继续神经网络系列。
强化学习:
强化学习也是一个很重要的方向了,很多人用强化学习玩游戏,可能有人觉得强化学习很难(包括我),但是我今天用网上流传很广的、很经典的一个例子(悬崖徒步, CliffWalking),去带领大家明白强化学习,大概分为两期(本期和下一期)讲明白这个例子。
今天就从最简单的方式:表格型入手,开始入门强化学习。
什么是强化学习?
强化学习是Reinforcement Learning,我也不知道为什么把Reinforcement翻译成强化,按照我的英语水平,inforce(应该是通enforce)是强迫,re-代表又,就是一再强迫,就是强迫一个东西一遍又一遍的学习。这也突出了强化学习的本质:一遍又一遍。
就好像小时候我们玩红白机,super mario的时候,一遍又一遍的玩,我们玩那个游戏的过程就可以成为强化学习的过程。我们玩的时候,每次死亡都能知道下一次应该怎么做,包括,哪一个管道可以蹲下去,得到很多金币,都会被我们探索出来,这些都在强化学习中会有体现。
和mnist手写数字识别那种学习方式的不同?
最明显的一个区别就是,我给出一张mnist数据集的图片,能清楚的知道他的正确答案是什么。而我给出一个RL的场景,很少有人能直接给正确(或者最优)方案。
比如给出一个mario在水管上(这个水管可以蹲下去吃金币)的场景,问这个场景最有解决方案,应该至少会有下面三个版本:
1. 应该蹲下去,因为金币很多,还能省很大一段路。
2. 应该继续走,前面有个加命的蘑菇。
3. 你们俩都太弱了,慢慢的掐距离,可以做到蘑菇吃完回来蹲进水管。
至于更多的方案,我玩的还是太少了,留给大家探索吧。
而mnist数据集这种有监督学习,给出场景,答案就是确定的,这个确定的答案(groundtruth)就是标签(label),被用来计算损失从而让学习有进程。
强化学习的过程,由于没有正确答案,只能一次又一次(reinforcement)的玩,然后被驱动着通关。
强化学习的驱动是什么?
奖励!
如mario游戏,吃金币+命,吃绿蘑菇也+命,两个都吃加更多的命。但是这些都是次要的,主要是通关。所以一般都会把通关的奖励设置的很高,死亡的奖励设置的很低。
当然,有些人喜欢探索环境,说明他们把其他的奖励设置的很高,比如发现密道(如哪个管道能蹲下去)等。
CliffWalking 悬崖徒步
环境说明
环境设定
这个环境是一个4x12的环境,游戏角色(agent)从坐标(3, 0)出生,目的是达到对面(3, 11),

如图,cliff是悬崖,掉进去就死亡。
当然,这个任务非常简单(对于人类来讲),一般的人类能一眼看到最优路径,但是电脑不会,电脑只能通过一遍又一遍的(reinforcemental)学习从而知道怎么解决这个任务(甚至不一定是最优方案)。
在这里有一些设定:超过边缘视为无动作。如(0, 0)处向左向上走,视为这一步是停止。如此,这就是今天要涉及到的环境了。
奖励驱动设定
不同的奖励驱动达到的目标效果不一样,如果想让他尽早达到终点,可以让他每走一步给出负奖励,他为了让奖励最大化,就能尽早走到终点。如果想让他多走几个格子,可是让他每走到一个和当前路径不相交的位置时给一个正奖励,他应该(因为我没试过)会走遍格子最后到终点。
到达终点给正奖励,掉下悬崖给负奖励这就不说了。
环境代码
# -*- coding: utf-8 -*-
import random
import numpy as np
import gym
from gym import spaces
"""
nrows
0 1 2 3 4 5 6 7 8 9 10 11 ncols
---------------------------------------
0 | | | | | | | | | | | | |
---------------------------------------
1 | | | | | | | | | | | | |
---------------------------------------
2 | | | | | | | | | | | | |
---------------------------------------
3 * | cliff | ^ |
*: start point
cliff: cliff
^: goal
"""
class CustomCliffWalking(object):
def __init__(self, stepReward: int=-1, cliffReward: int=-10, goalReward: int=10) -> None:
self.sr = stepReward
self.cr = cliffReward
self.gr = goalReward
self.action_space = spaces.Discrete(4) # 上下左右
self.pos = np.array([3, 0], dtype=np.int8) # agent 在3,0处出生,掉到悬崖内就会死亡,触发done和cliffReward
def reset(self, random_reset=False):
"""
初始化agent的位置
random: 是否随机出生, 如果设置random为True, 则出生点会随机产生
"""
x, y = 3, 0
if random_reset:
y = random.randint(0, 11)
if y == 0:
x = random.randint(0, 3)
else: # 除了正常坐标之外,还有一个不正常坐标:(3, 0)
x = random.randint(0, 2)
# 严格来讲,cliff和goal不算在坐标体系内
# agent 在3,0处出生,掉到悬崖内就会死亡,触发done和cliffReward
self.pos = np.array([x, y], dtype=np.int8)
def step(self, action: int) -> list[list, int, bool, bool, dict]:
"""
执行一个动作
action:
0: 上
1: 下
2: 左
3: 右
"""
move = [
np.array([-1, 0], dtype=np.int8), # 向上,就是x-1, y不动,
np.array([ 1, 0], dtype=np.int8), # 向下,就是x+1, y不动,
np.array([0, -1], dtype=np.int8), # 向左,就是y-1, x不动,
np.array([0, 1], dtype=np.int8), # 向右,就是y+1, x不动,
]
new_pos = self.pos + move[action]
# 上左不能小于0
new_pos[new_pos < 0] = 0 # 超界的处理,比如0, 0 处向上或者向右走,处理完还是0,0
# 上右不能超界
if new_pos[0] > 3:
new_pos[0] = 3 # 超界处理
if new_pos[1] > 11:
new_pos[1] = 11
reward = -1
die = False
win = False
info = {
"reachGoal": False,
"fallCliff": False,
}
die = self.__is_pos_die(new_pos.tolist())
if die:
info["fallCliff"] = True
reward = self.cr
win = self.__is_pos_win(new_pos.tolist())
if win:
info["reachGoal"] = True
reward = self.gr
self.pos = new_pos # 更新坐标
return new_pos, reward, die, win, info
def __is_pos_die(self, pos: list[int, int]) -> bool:
"""判断自己的这个状态是不是已经结束了"""
return pos in [
[3, 1],
[3, 2],
[3, 3],
[3, 4],
[3, 5],
[3, 6],
[3, 7],
[3, 8],
[3, 9],
[3, 10],
[3, 11],
]
def __is_pos_win(self, pos: list[int, int]) -> bool:
"""判断自己的这个状态是不是已经结束了"""
return pos in [
[3, 11],
]
学习方式
现在有了环境,有了驱动,怎么学习呢?
时序差分算法
时序差分算法其实很简单:
比如还是mario站在管道上(这个场景记为S_now),区分两种情况(两种动作,a):1)蹲下去;2)向前走。
1) :mario这时候想,蹲下去有很多金币(假设每个奖励是1,下面差不多有不到30个,按照50个算吧),回报是50,然后还不容易死(99%通关吧,1%死),通关回报又是50,死亡回报-100。
即:当前状态+蹲下去 -> 吃很多金币得到50 -> 可能通关可能死的回报 0.99*50 + 0.01* (-100)=48.5.
但是由于通关太远了,所以现在应该打折扣,比如有一个折扣因子(discount factor)γ=0.9,所以当前状态下蹲下去的期望总回报是:50 + γ * 48.5 = 93.65的回报。
2) mario这时候想,我向前走可以多条命,虽然容易死,但是只要不死就是多条命,何乐而不为呢?一条命是100金币,回报就是100,但是通关的概率是50%,通关是50回报。死亡是 -100 回报(因为少了条命)。
即:当前状态+继续走 -> +1条命是100回报 -> 可能通关可能死的回报 0.5*50+0.5*(-100)=-25。
所以当前向前走的期望总回报是:100 + γ * (-25) = 77.5。
假设mario走第一条路,所以当前状态下他下蹲的期望回报Q(S_now, 下蹲)(Q就是当前状态下他下蹲的期望回报)就是93.65。
然后他下蹲,拿到了管道下的金币奖励50,出了管道,然后他面临两个蘑菇(这个时候记为S_next)。这时候他面临:
当前状态+撞上去(假设他之前算的不对,发现避不开了,自己死亡的概率是100%) -> 立死 -100
当前状态+跳过去 (假设他之前算的不对,现在发现存活概率是0%)-> 肯定能通关了+50
这俩的期望回报(也就是V(S_next))是:-100(虽然有些极端,但是能理解就行)。
到这里,有两个数据:
1. 走了一步之后的立即回报50(记为R) + gamma * 下一个状态下的期望回报(V(S_next))-100共-40.
2. (贪心的mario)走之前算的那时候的期望回报(V(S_now))是93.65
V(S_now):可以看作是,我认为我可以得到这么多奖励。
Q(S_now, a):我认为我执行a动作可以得到这么多奖励
R +V(S_next):可以看作是:我实际上可以得到这么多奖励。
这时就可以求出误差:error = R + V(S_next) - V(S_now) = -40 - 93.65 = -133.65,就知道自己计算的差别在哪了。
然后可以设一个学习率因子 lr = 0.5,更新 Q(S_now, a)。
Q(S_now, a) = Q(S_now, a) + lr * error = 93.65 - 0.5 * (-133.65)
这个error,就是时序误差。按照这样的方式,agent就能一遍又一遍地(reinforcementally)纠正自己的估计错误。直到自己估计正确。
SARSA
现在就要引入强化学习很经典的一个算法了:SARSA,是一个on-policy(这个国内翻译版本不是唯一的,所以我就不翻译了)的TD(时序差分,time difference)算法。
SARSA和上面差不多,只不过在S_next处会走一步,计算Q(S_next, a)进行计算误差更新。这也就是为啥他叫SARSA(S_now, action_now, reward, S_next, action_next)方式。
大概是:
Q(S_now, action_now) = Q(S_now, action_now) +
lr * (Reward_now + gamma * Q(S_next, action_next) - Q(S_now, action_now) )
今天就会使用SARSA算法进行这个cliffwalking的更新。
强化学习代码(表格型)
由于这个Cliff Walking任务很简单,可以用一个表格来模拟,这样的话,更直观,容易理解。
这个任务是4*12的表格,每个位置有四个动作,所以形状是4x12x4
Q = np.zeros((4, 12, 4), dtype=np.float32) # 价值表格,然后实例化环境:
cw = CustomCliffWalking(stepReward=sr, cliffReward=cr, goalReward=gr)然后根据上面的更新公式实现代码,完整代码如下:
# -*- coding: utf-8 -*-
import random
import numpy as np
from env.cliffwalking import CustomCliffWalking
import matplotlib.pyplot as plt
nepisodes = 100000 # total 10w episodes
epsilon = 0.05 # epsilon greedy policy
gamma = 0.9 # discount factor
lr = 0.1
random_reset = False
seed = 42
sr = -1
cr = -10
gr = 10
def select_action(Q: np.ndarray, pos: np.ndarray, nact: int, epsilon=0) -> int:
"""选择动作,默认是贪心,"""
# epsilon贪心算法选择动作,也可以把epsilon设置为0,就是完全贪心选择动作
if random.random() < epsilon:
action = random.randint(0, nact-1)
else: # 按照表格选取动作,如果多个动作价值一样,则取下标靠前的
action = np.argmax(Q[pos[0], pos[1], :])
return action
def main():
"""实现悬崖徒步,表格形式的"""
np.random.seed(seed=seed)
random.seed(seed)
Q = np.zeros((4, 12, 4), dtype=np.float32) # 价值表格,
cw = CustomCliffWalking(stepReward=sr, cliffReward=cr, goalReward=gr) # 实例化环境
nact = cw.action_space.n
for i in range(1, nepisodes + 1):
if i % 1000 == 0:
print("{}/{}".format(i, nepisodes))
cw.reset(random_reset=random_reset) # 不随机产生位置,随机应该更好一点,这里不随机产生了
steps = 0
while True:
steps += 1
old_pos = cw.pos # 保留旧的位置,也就是 S_now
action = select_action(Q=Q, pos=old_pos, nact=nact, epsilon=epsilon) # 也就是 action_now
# print(new_pos, reward, die, win, info)
new_pos, reward, die, win, info = cw.step(action=action)
# 这里得到了 S_next 和 Reward_now
action_next = select_action(Q=Q, pos=new_pos, nact=nact, epsilon=epsilon)
# 这里是 action_next
# 如果死了或者过关了,那么就没有后续了,就不需要后面的了
actual_reward = reward + (1-(die or win)) * gamma * Q[new_pos[0], new_pos[1], action_next]
# 计算走一步的instant + gamma * Q(S_next, a_next)
target_reward = Q[old_pos[0], old_pos[1], action] # Q(S_now, a)
# print("target_reward:", target_reward)
bellman_error = actual_reward - target_reward # 计算估计的误差
Q[old_pos[0], old_pos[1], action] = Q[old_pos[0], old_pos[1], action] + lr * bellman_error
# Q(S_now, action_now) = Q(S_now, action) + lr * 误差
if die or win:
break # 胜利或失败
# 训练完了,具象化显示学习到的价值
for i in range(nact):
plt.subplot(nact, 1, i+1)
plt.imshow(Q[:, :, i])
plt.axis('off')
plt.colorbar()
if i == 0:
plt.title("up")
elif i == 1:
plt.title("down")
elif i == 2:
plt.title("left")
elif i == 3:
plt.title("right")
plt.savefig("./out/table/Q_sarsa_"+str(sr)+"_"+str(gr)+"_"+str(cr)+".png")
plt.clf()
plt.close()
path = np.zeros((4, 12), dtype=np.float64)
cw.reset()
x = cw.pos[0]
y = cw.pos[1]
while True: # 走
# 贪心算法选择动作
action= np.argmax(Q[x, y, :])
print(x, y, action)
new_pos, reward, die, win, info = cw.step(action=action)
x, y = new_pos[0], new_pos[1]
if win:
print("[+] you win!")
break
if die:
print("[+] you lose!")
break
x = new_pos[0]
y = new_pos[1]
if x >= 0 and x <= 3 and y >= 0 and y <= 11:
path[x, y] = 1.0
plt.imshow(path)
plt.colorbar()
plt.savefig("./out/table/path_sarsa_"+str(sr)+"_"+str(gr)+"_"+str(cr)+".png")
# 保存学习到的价值
np.savetxt("out/table/cliff_walking_table_{}_{}_上.csv".format(gr, cr), Q[:,:,0],
delimiter="\t", fmt="%.2f")
np.savetxt("out/table/cliff_walking_table_{}_{}_下.csv".format(gr, cr), Q[:,:,1],
delimiter="\t", fmt="%.2f")
np.savetxt("out/table/cliff_walking_table_{}_{}_左.csv".format(gr, cr), Q[:,:,2],
delimiter="\t", fmt="%.2f")
np.savetxt("out/table/cliff_walking_table_{}_{}_右.csv".format(gr, cr), Q[:,:,3],
delimiter="\t", fmt="%.2f")
if __name__ == "__main__":
main()结果
我的CPU还是很快就运行完了,,因该也不会太慢。。如果你的太慢,我试了试,一万个回合的结果也收敛了。
(注意:运行时确保环境内无其他程序使用matplotlib,否则会出现闪退情况)
价值计算图

行走路径图
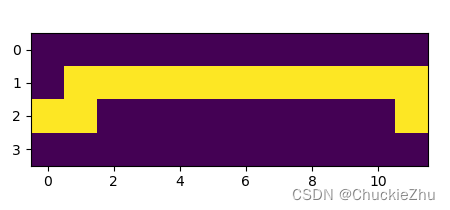
计算的价值结果
这个是每个位置向上的价值。

这个是每个位置向下的价值,可以看到,目标点上面向下都是10,悬崖上面向下都是-10,和我们的预期一样。
这个是每个位置向左的价值。可见,每一行越往左,这个价值越低,和我们预期也一样,因为越向左越远,按理来讲折扣价值就是更低。
这个是每个位置向右的价值,可见越向右价值越高。(除了地图边缘处向右是为了给自己多-1的惩罚)

结束语
本来想着稍微写一下,写完之后发现竟然达到了八千多字,应该分开写的,,下次我会加入神经网络的元素,希望大家看完能有所收获!