一、问题描述

问题描述：一辆虚拟汽车加满油后可行驶n km。旅途中有若干加油站。设计一个有效算法，指出应该在那些加油站停靠加油，使沿途加油次数最少。并证明算法的能产生一个最优解。

算法设计：对于给定的n和k个加油站位置，计算最少加油次数。

数据输入：有文件input.txt给出输入数据。第1行有两个正整数n 和 k ，表示汽车加满油后可行驶n km，且旅途中有k 个加油站。接下来的1行中有K+1个整数，表示第k个加油站与敌k-1个加油站之间的距离。第0个加油站表示出发地点，汽车已加满油。第k+1个加油站表示目的地。

结果输出：将计算的最少加油次数输出到文件output.txt。如果无法到达目的地，则输出“No Solution”。

//input.txt 输入内容

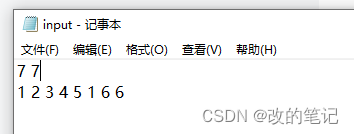
7 7

1 2 3 4 5 1 6 6

//output.txt 结果输出

4

二、问题剖析

该部分为什么会有0~K+1个加油站呢，下面的图可以很好帮助了解这个题目所需要解决的问题：

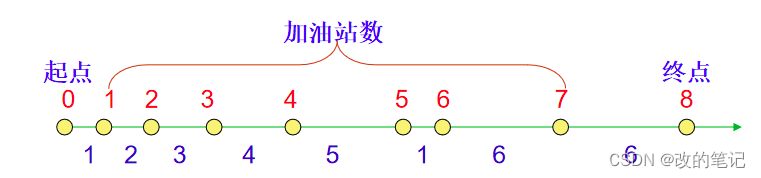
基本思想：

首先需要简单了解贪心算法的基本要素：最优子结构性质、贪心选择性质

根据一个贪心选择性，每当到达一个加油站的时候，都要进行一次判断，看看剩余的油量能不能维持到下一个加油站。也就是说如果剩余的油量咱们能到达下一站的话，就不加油了，继续前进；如果不行的话，更新邮箱的油量，加满

三、代码实现

#include<stdio.h>

int main()
{
  int n,k;
  
  freopen("input.txt","r",stdin);
  freopen("output.txt","w",stdout);
  
  scanf("%d %d",&n,&k);//从文件夹中取出加满油可行使的公里数n，和加油站数量k 

  int x[k+1];
  for(int i=0;i<k+1;i++) //从文件中取出两加油站之间的距离 
  {
  	scanf("%d",&x[i]);
  }
  
  int sum=0, count=0; // 加油后行驶总距离  加油次数

  for (int i = 0; i < k + 1; i++)//如果有两站之间的距离超过了汽车加满油后行驶的距离，输出No Solution 
  {
    if(x[i]>n)
    {
      printf("No Solution!");
      return 0;
    }
  }

  sum = x[0];//从第0个加油站加满油出发 

  for (int i = 1; i < k + 1; i++)
  {
    sum+=x[i];
    if (sum >= n) //如果剩余油量不够行驶下一路段 ，则加一次油 
    {
      count++;
      sum = x[i-1];
    }
  }

  printf("%d",count);

  return 0;
}