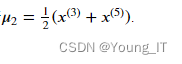目录
- 1. 介绍
- 2. 标准卷积
- 3. 转置卷积
- 4. 总结
1. 介绍
转置卷积(Transposed Convolution)经常也被称作反卷积,所谓反卷积即为通过标准卷积层生成的输出被反卷积,将得到原始输入。而转置卷积不按值反转标准卷积,而仅按维度。

转置卷积层和标准卷积层的计算原理完全相同,不同的是输入特征图不同。下面分别介绍标准卷积和转置卷积。转置卷积怎么来的请参考:https://blog.csdn.net/tsyccnh/article/details/87357447,这篇博客只介绍转置卷积的具体实现。
2. 标准卷积
输入特征图大小为 i × i i\times i i×i 的标准卷积层由以下两个参数定义:
- Padding (p):对特征图周围进行填充,扩大到 ( i + 2 ∗ p ) × ( i + 2 ∗ p ) (i+2 * p )\times (i+2*p) (i+2∗p)×(i+2∗p);
- Stride (s):卷积核在特征图上移动的步长。
下图展示了一个卷积层是如何分两步进行的:

在第一步中,输入特征图用零填充,而在第二步中,卷积核通过前面定义的步长在特征图上进行滑动,并于滑动窗口求点积。卷积层有 “Same” 和 “Vaild” 卷积,前者输出的空间维度等于输入的空间维度,后者输出的空间维度小于输入的空间维度,在搭建模型中,一般使用 “Same” 卷积。下面的动画演示了不同 Stride 和Padding 的卷积层。




o = i + 2 p − k s + 1 o = \frac{i + 2p - k}{s} + 1 o=si+2p−k+1
3. 转置卷积
转置卷积通常用于上采样,即生成空间维度大于输入特征图的输出特征图。就像标准卷积层一样,转置卷积层也由 Padding 和 Stride 定义。Padding 和 Stride 的这些值是假设在输出上执行以生成输入的值。也就是说,如果您获取输出,并执行定义了步长和填充的标准卷积,它将生成与输入相同的空间维度。
转置卷积的实现过程有下面四步:
- 计算 p ′ p' p′ 和 z z z,其中 p ′ = k − p − 1 , z = s − 1 p' = k - p - 1,z = s - 1 p′=k−p−1,z=s−1, k , p , s k,p,s k,p,s 分别为卷积核大小,输入的参数 Padding 和 输入的参数 Stride, p ′ , s ′ p', s' p′,s′ 分别为转置卷积在进行卷积操作时的填充大小和步长;
- 在输入特征图的行行和列列之间,插入 z z z 个零,使得输入特征图大小为 2 i − 1 × 2 i − 1 2i - 1 \times 2i - 1 2i−1×2i−1;
- 对第二步中得到的特征图进行 Padding,大小为 p ′ p' p′;
- 对第三步中生成的图像进行标准卷积,步长为 1。

下面的动画演示了不同 Stride 和Padding 的转置卷积层

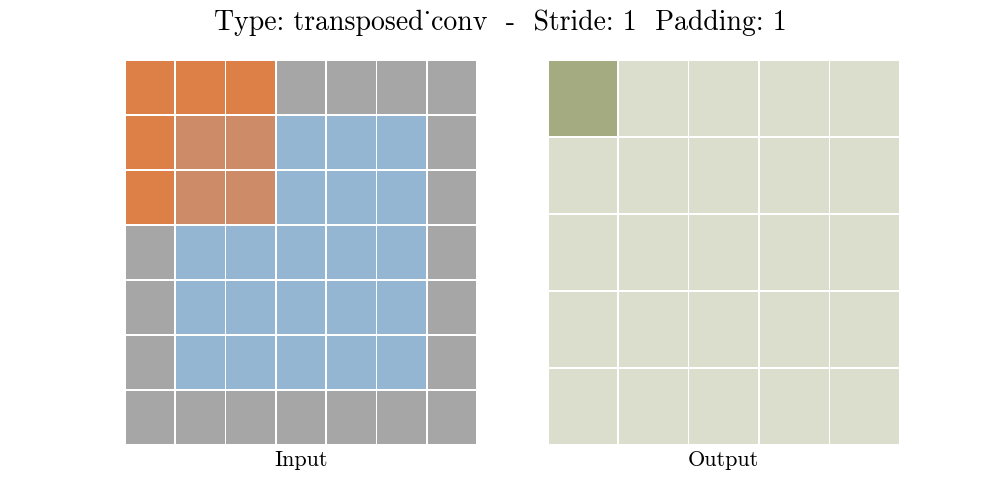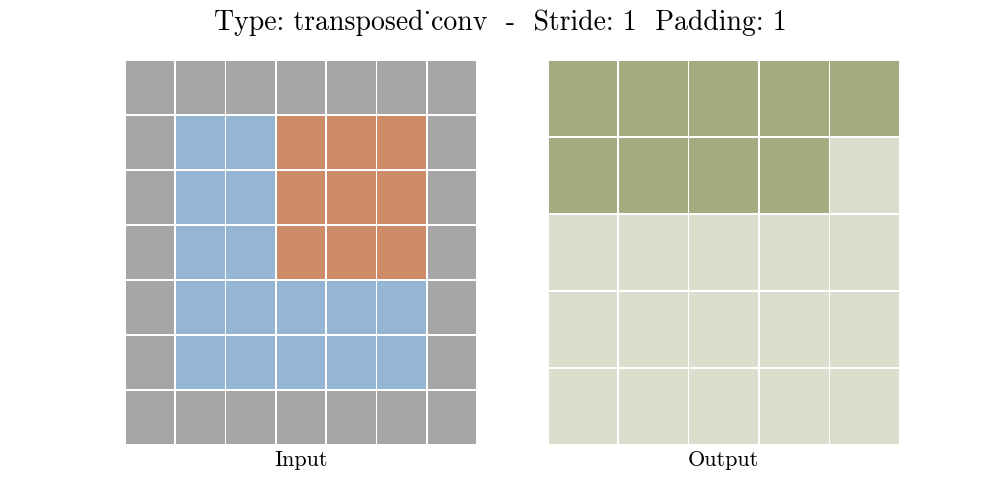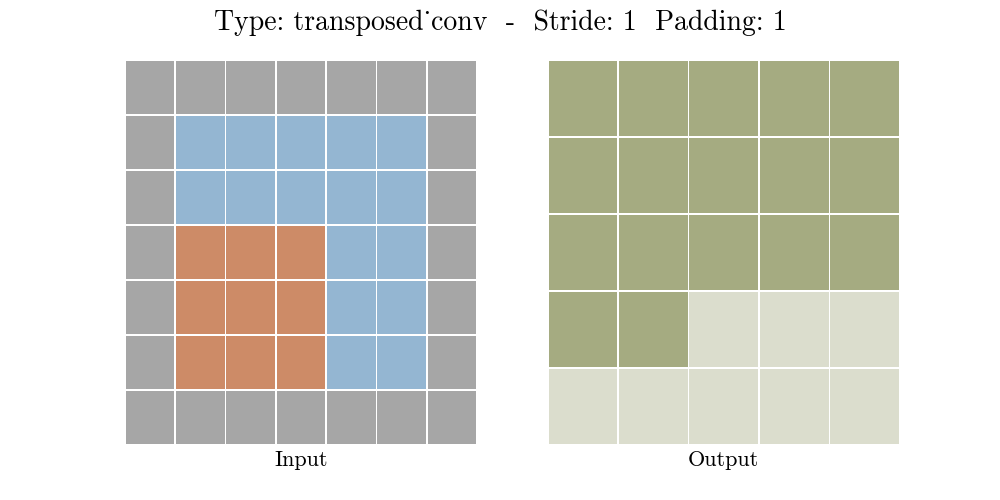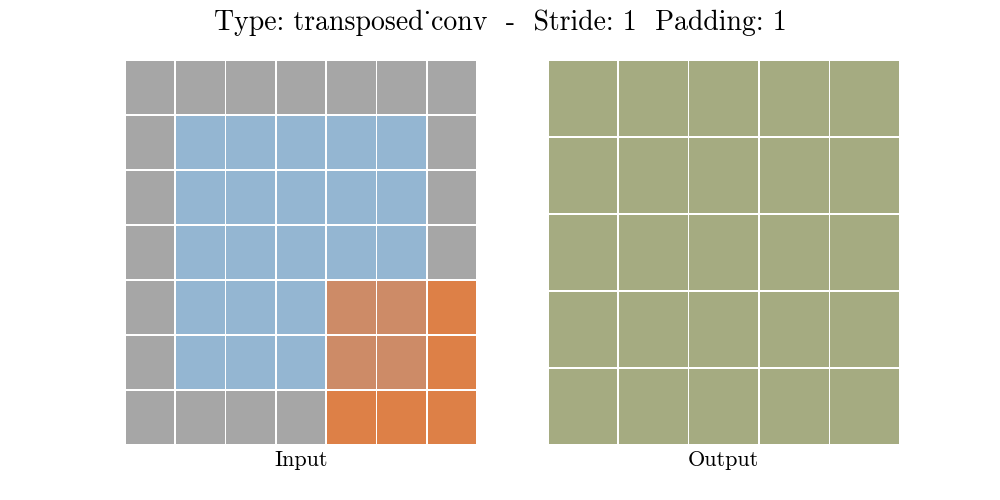

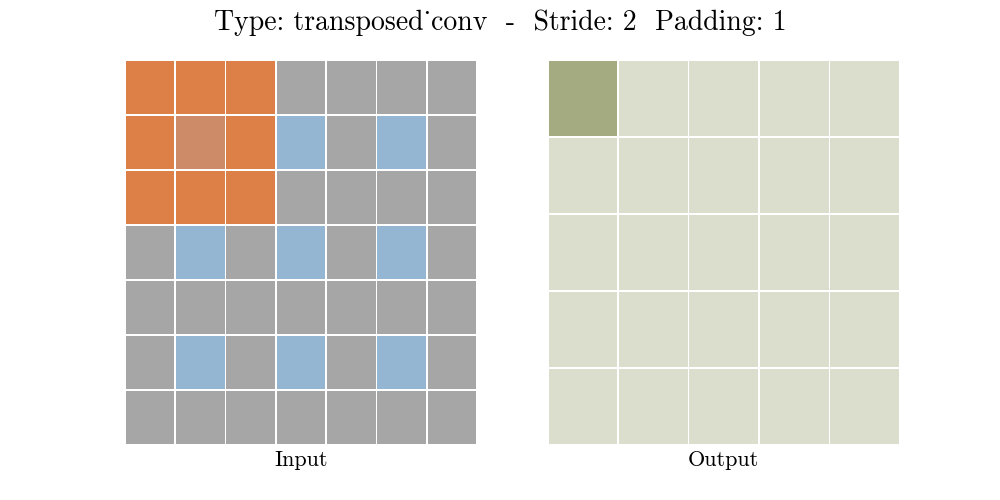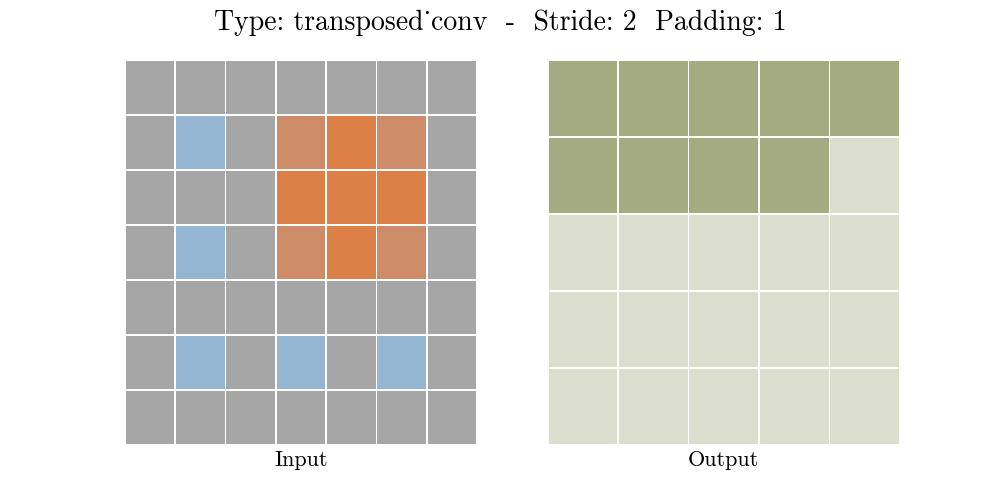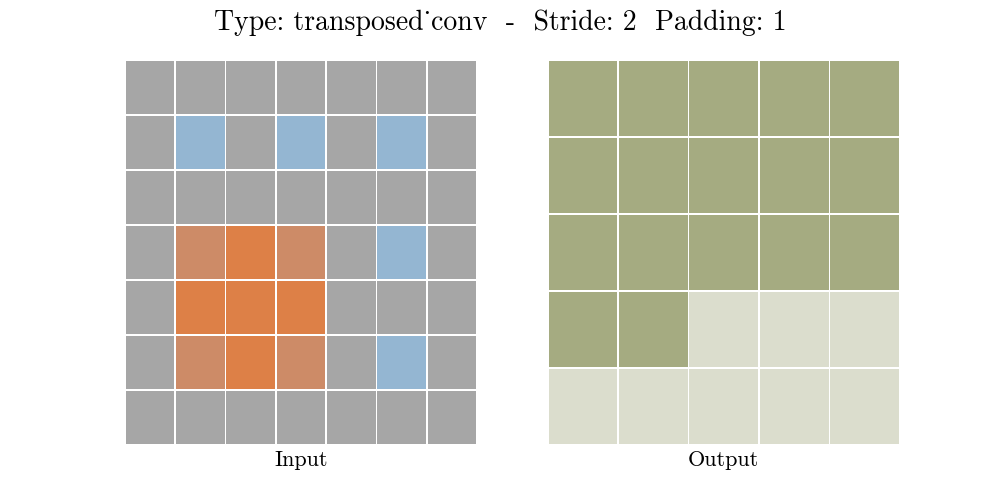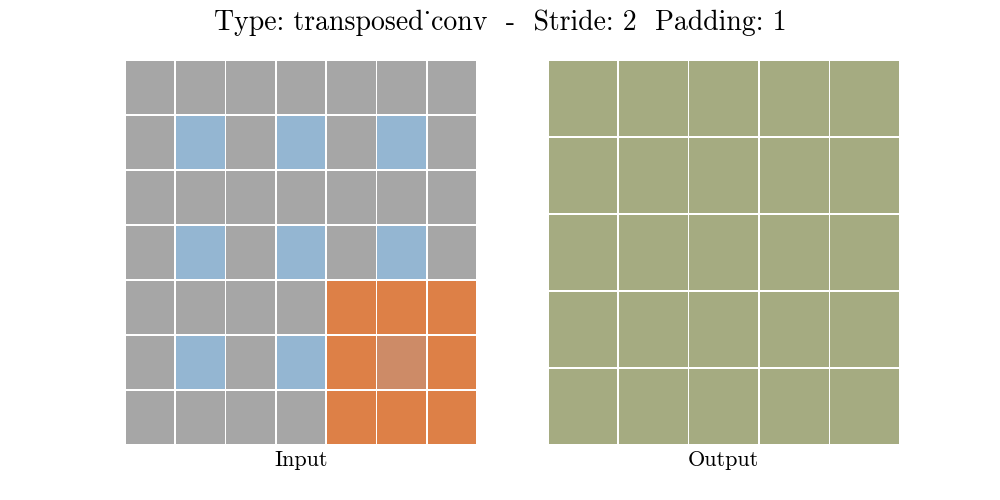
o = ( i − 1 ) × s + k − 2 p o = (i - 1) \times s + k - 2p o=(i−1)×s+k−2p
4. 总结
标准卷积和转置卷积总结如下:

- 转置卷积的用处主要是对特征图进行上采样;
- 转置卷积其实也是一种标准卷积,只不过要先根据输入的参数对输入特征图进行修改,也就是填充操作;
- 转置卷积在滑动点积操作时的 Padding 和 Stride 参数与输入参数不同,其中 p ′ = k − p − 1 , s ′ = 1 p' = k - p - 1, s' = 1 p′=k−p−1,s′=1。