【加解密篇】Passware Kit Forensic暴力美学-已知部分密码自定义解密详细参数设置
都说"自制武器不一定是最强的,但最强的武器一定是自制的",对于取证工具也是一样,虽然默认配置足够强,但如果我们能根据实时情景自定义参数配置,那么往往能事半功倍—【蘇小沐】
文章目录
- 【加解密篇】Passware Kit Forensic暴力美学-已知部分密码自定义解密详细参数设置
- 1.实验环境
- 2.RAR加密压缩包
- (一)指定常规密码格式
- 1、选择加密文档
- 2、三种破解模式
- (二)已知部分密码自定义解密设置
- 1、方法一:字典破解
- 2、方法二:自定义暴力破解【推荐】
- (三)暴力破解错误示范
- 1、参数设置错误1:密码长度
- 2、已知密码部分未设置全
- 3、勾选了自定义字符(Custom characters)
- *其他破解方法
- 总结
- 参考资料
1.实验环境
| 系统 | 版本 |
|---|---|
| Windows 11 专业工作站版 | 22H2(22621.1702); |
| Passware Kit Forensic | 2019.4.1; |
2.RAR加密压缩包
已知RAR压缩包的密码规则:wlzhg@xxxx@xn,其中xxxx部分是需要破解的部分。
(一)指定常规密码格式
1、选择加密文档
常规就是选择需要解密的文档,点击。
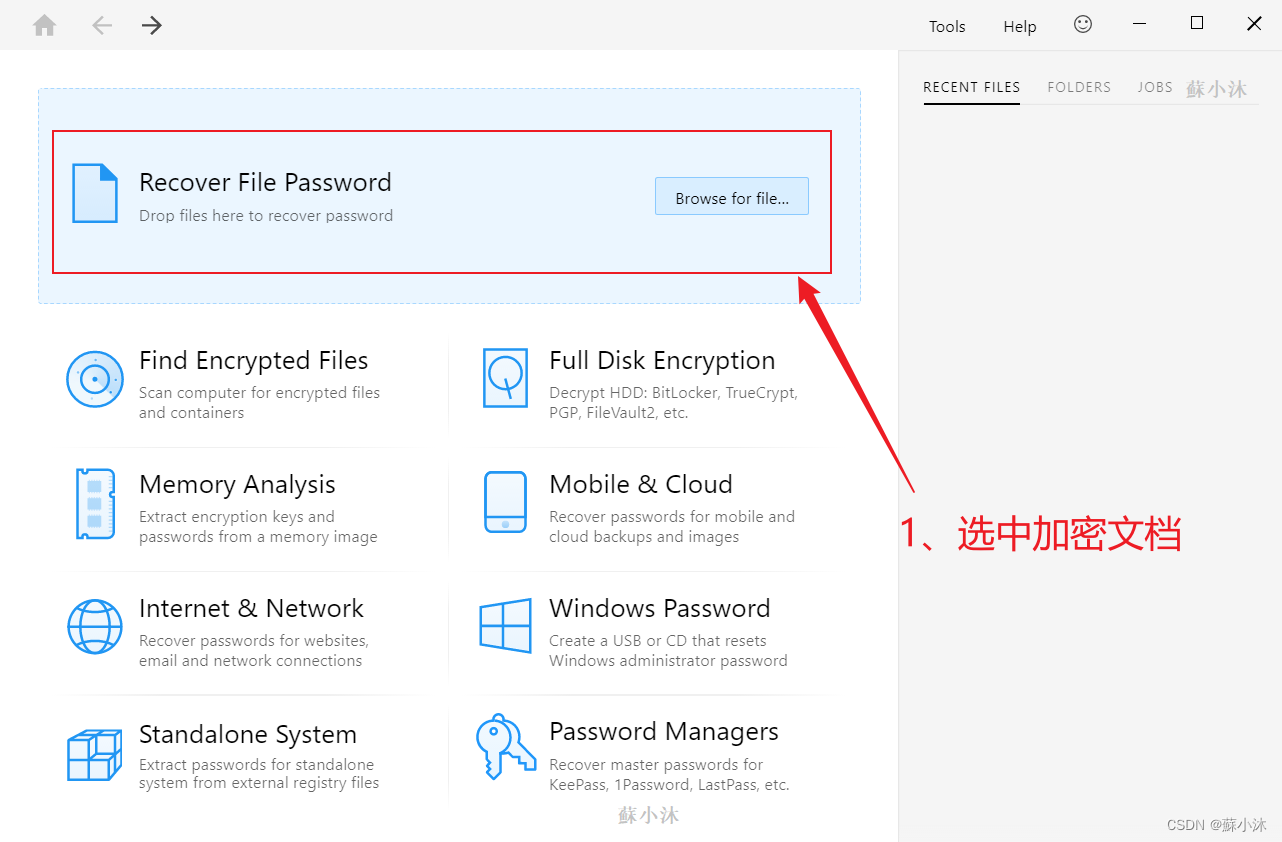
2、三种破解模式
最初的向导屏幕如下所示,Passware Kit提供了三种破解模式。
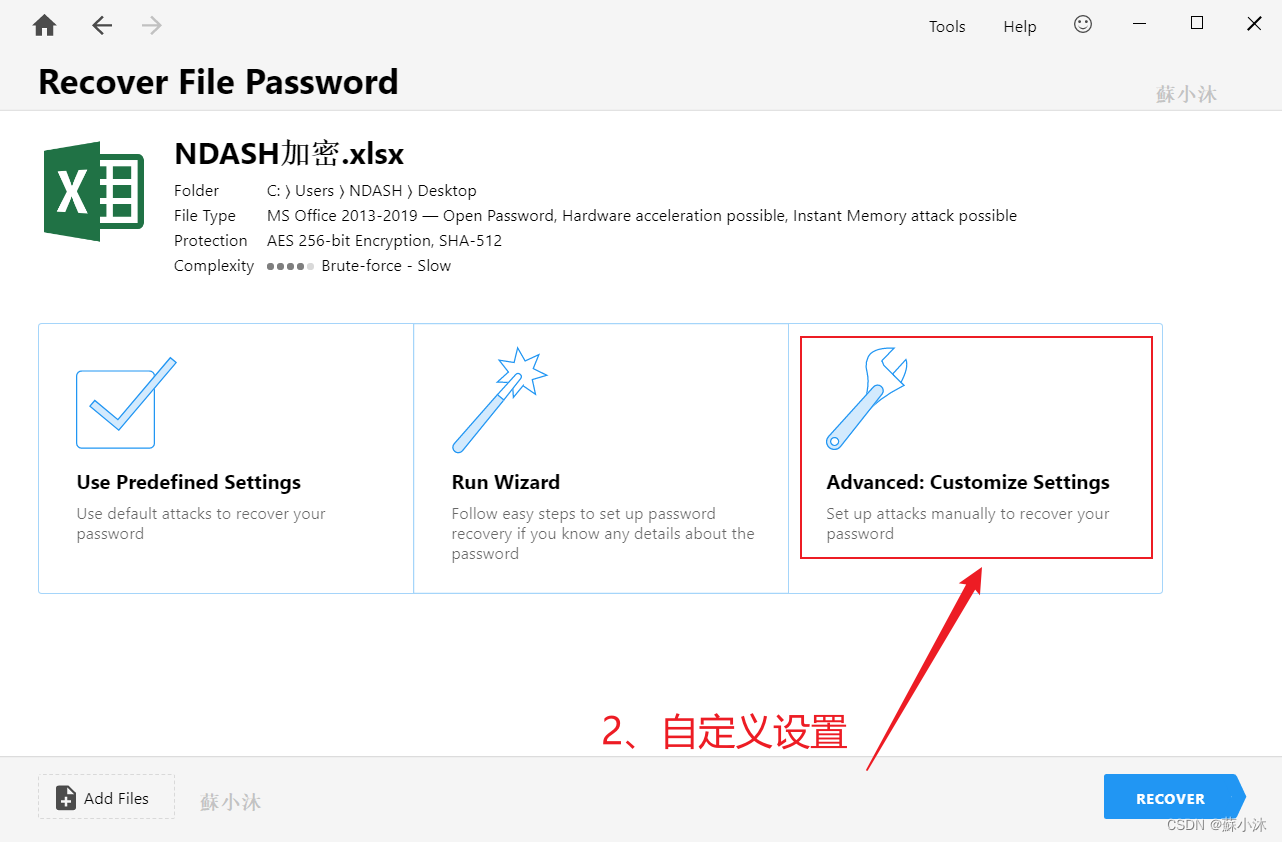
| 参数 | 说明 |
|---|---|
| 使用预定义设置 | 预定义设置是对于密码完全没有信息的,使用默认攻击恢复密码。 |
| 运行向导 | 如果您知道有关密码的任何细节,请按照简单的步骤设置密码恢复,适用于知道密码部分信息的破解方法。 |
| 高级:自定义设置 | 手动设置攻击以恢复您的密码,自定义破解密码参数。 |
根据文件格式,优先设置破解密码的类型、密码长度、密码结构(组合类型)等,点击保存,完成开始破解密码。

(二)已知部分密码自定义解密设置
暴力破解设置:密码开头wlzhg@,密码结尾是@xn,中间缺少4位数字,所有密码长度为13。
根据已知条件,可以直接设置为:wlzhg@*@xn。【星号*和问号?有些区别,可以自行尝试,建议使用星号*】
二选一即可,更推荐第二种方式,第一种字典破解更适合了解密码组成规律,然后自生成的字典。

1、方法一:字典破解
字典参数设置:密码长度最长为13。(因为是比赛,直接13to13更精确)
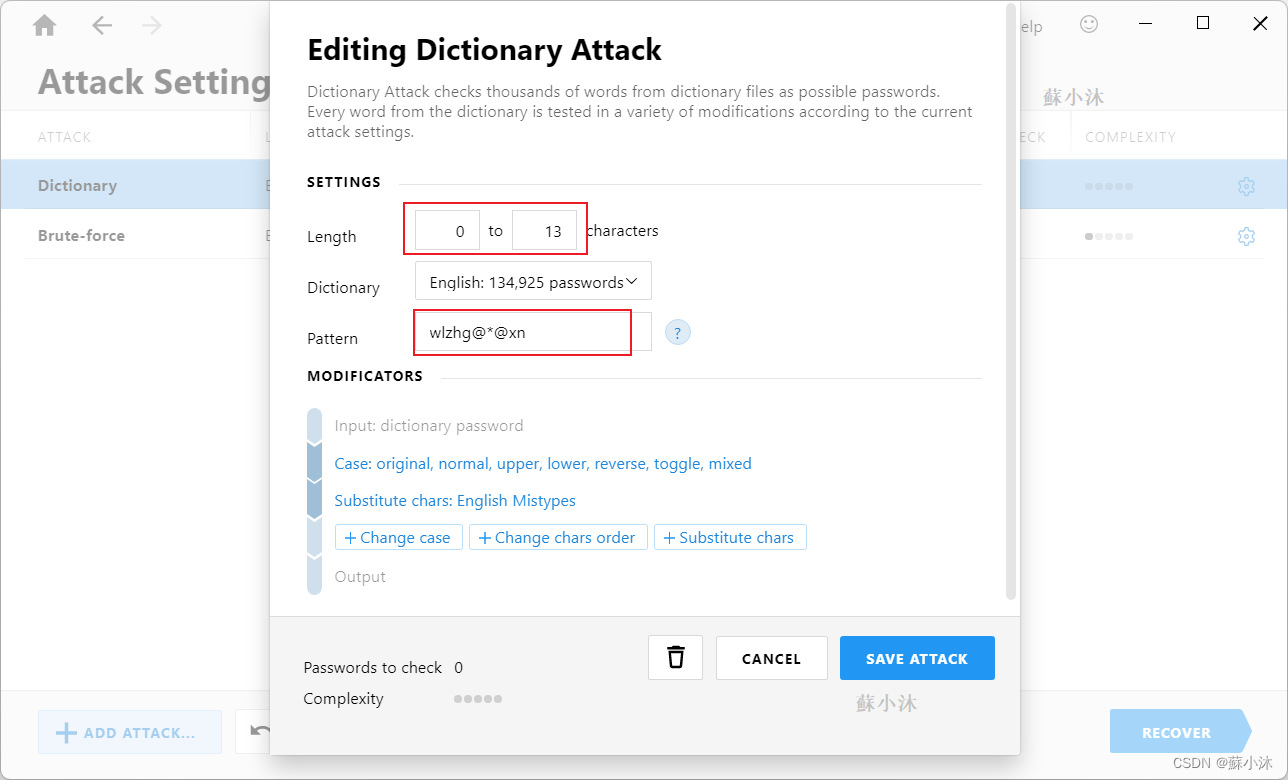
2、方法二:自定义暴力破解【推荐】
高级设置:自定义字符(Custom characters)和模式(Pattern)。
选择第二个模式(Pattern)!!!只有一千次的尝试,基本是秒破解。
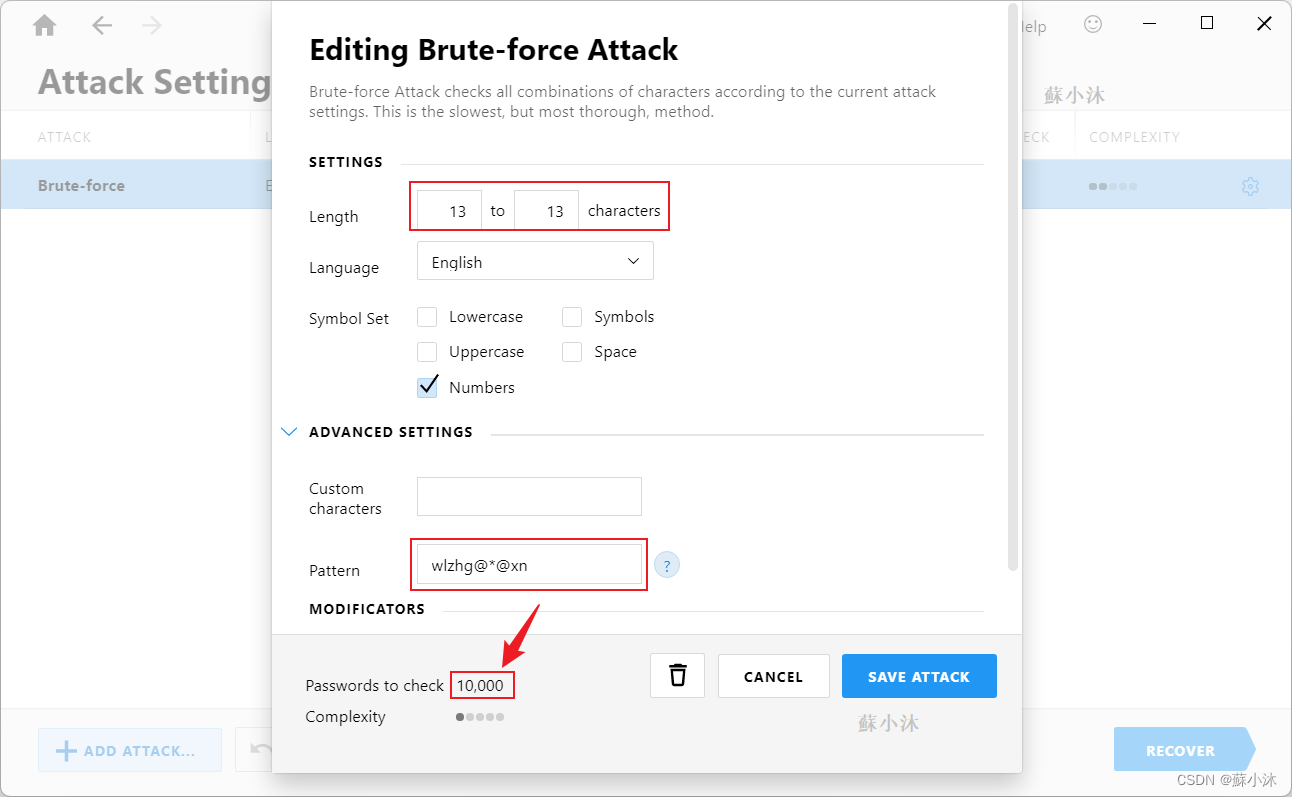
(三)暴力破解错误示范
不一定错,而是不同场景使用不同;示警,减少不必要的麻烦。
1、参数设置错误1:密码长度
因为是打比赛,已经明确给出了密码位数及所缺的位数,就按照给定的来设置密码长度位数即可,不要画蛇添足,浪费时间。
当然,如果是不确定密码长度,可以多尝试,但花费时间较多。

2、已知密码部分未设置全
因为密码缺少的是中间部分,第一个设置的参数是字典破解(本地未链接字典)。其次在已知部分,漏掉了密码字典的后半部分,导致破解次数几何式增长,浪费时间和算力。
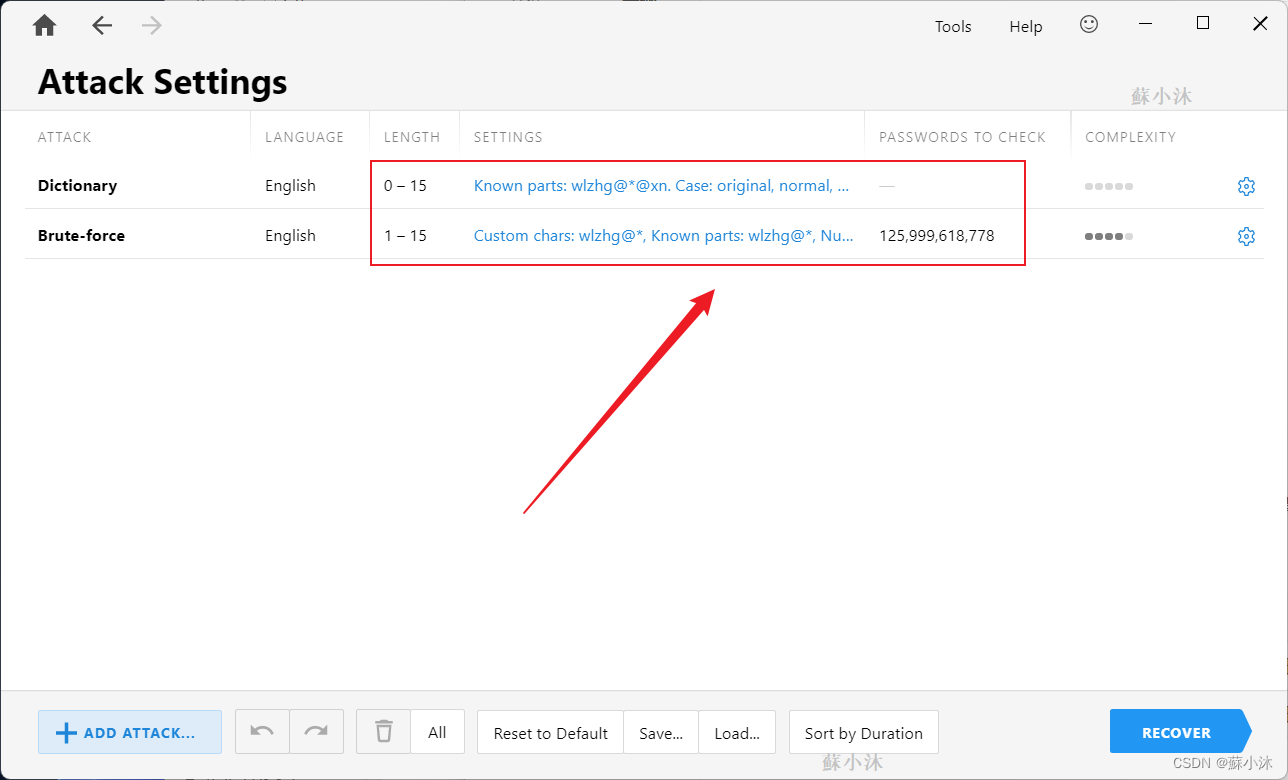
3、勾选了自定义字符(Custom characters)
此次测试中,虽然使用PasswareKit也是秒破,但勾选后尝试次数达到137561次,比单勾选模式(Pattern)多了十几倍;对于一些未知的密码,需要耗时更多,一般清楚部分密码不建议勾选该选项。
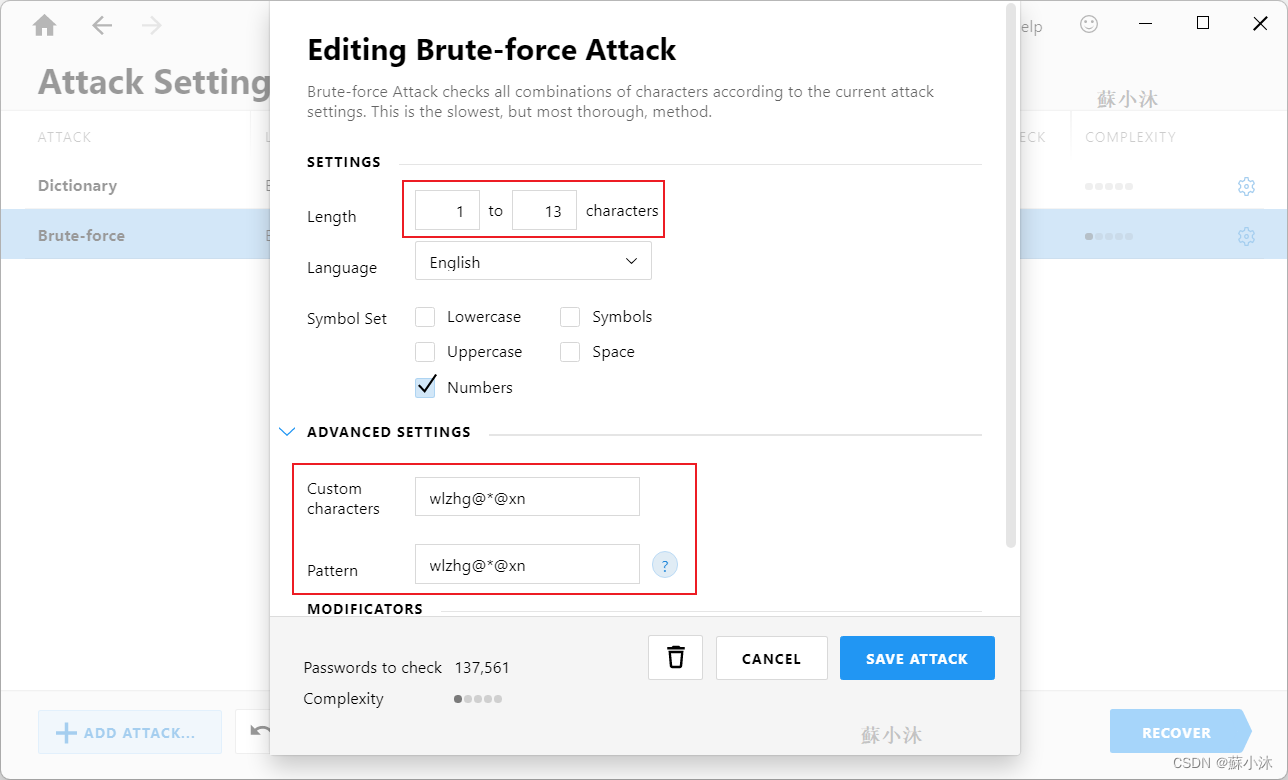
因为只有4位数,很快就能破解出来。
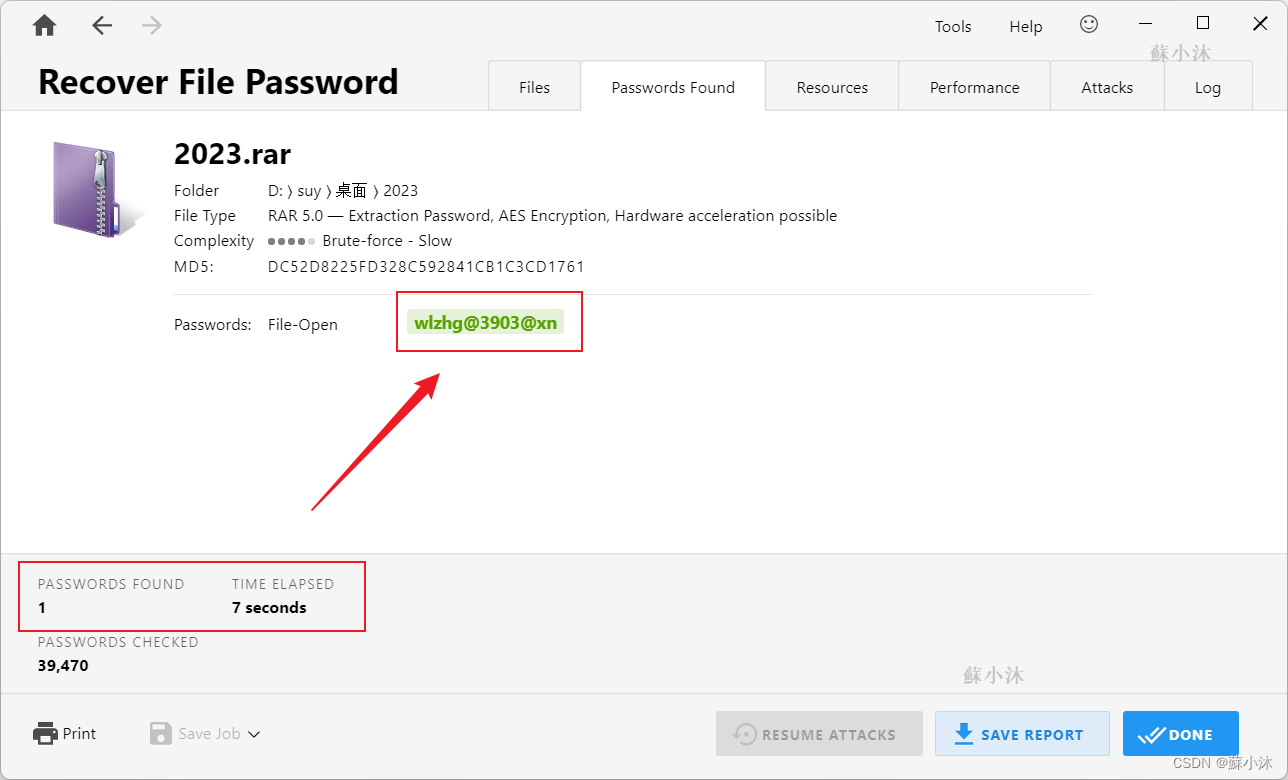
*其他破解方法
【加解密篇】利用HashCat破解RAR压缩包加密文件详细教程 -文章频道 - 密码学 - 公开学习圈 (writebug.com)
【加解密篇】利用HashCat破解RAR压缩包加密文件详细教程_蘇小沐的博客-CSDN博客
总结
有时间多尝试一步或许就可以得到答案。
书写片面,纯粹做个记录,有错漏之处欢迎指正。
【著作所有权归作者 [蘇小沐] 所有,转载请注明文章出处】
参考资料
Passware Kit Forensic在已知部分密码的情况下破解全部密码_知远同学的博客-CSDN博客
【加解密篇】Passware Kit Forensic纯数字密码破解教程_passwarekit产品密钥_蘇小沐的博客-CSDN博客
【加解密篇】Passware Kit Forensic自定义解密类型教程_蘇小沐的博客-CSDN博客
| 名称 | 时间 |
|---|---|
| 开始编辑日期 | 2021 年 09 月 02 日 |
| 最后编辑日期 | 2023 年 05 月 11 日 |