第 46 届国际大学生程序设计竞赛（ICPC）亚洲区域赛（上海），签到题6题

文章目录

- - E.Strange Integers
  - D.Strange Fractions
  - G.Edge Groups
  - I.Steadily Growing Steam
  - H.Life is a Game
  - K.Circle of Life

补题链接：https://codeforces.com/gym/103446

E.Strange Integers

E. Strange Integers
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Given n integers A1,A2,⋯,An and a parameter k, you should choose some integers Ab1,Ab2,⋯,Abm(1≤b1<b2<⋯<bm≤n) so that ∀1≤i<j≤m,|Abi−Abj|≥k. Determine the maximum number of the integers you can choose.

Input
The first line contains two integers n,k(1≤n≤105,0≤k≤109), denoting the number of given integers and the given parameter.

The second line contains n integers A1,A2,⋯,An(1≤Ai≤109), denoting the given integers.

Output
Output one line containing one integer, denoting the maximum number of the integers you can choose.

Example
inputCopy
11 2
3 1 4 1 5 9 2 6 5 3 5
outputCopy
4
Note
One possible scheme is to choose {A3=4,A6=9,A7=2,A8=6}.

题意：

给你n个数，从中选出m个，满足任意两个数的绝对值之差大于等于k
求m的最大值。

思路：

贪心的将原序列排个序，先选一个最小值t，然后扫一遍，每次选大于等于t+k的最小值即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int a[N];

int main(){
    int n, k;  cin>>n>>k;
    for(int i = 1; i <= n; i++)cin>>a[i];
    sort(a+1,a+n+1);
    int t = a[1], res = 1; 
    for(int i = 2; i <= n; i++){
        if(a[i]>=t+k){
            t = a[i];
            res++;
        }
    }
    cout<<res<<"\n";
    return 0;
}

D.Strange Fractions

D. Strange Fractions
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Given a positive fraction pq, you should find two positive integers a,b that pq=ab+ba. If no such integers, report it.

Input
The first line contains one integer T(1≤T≤105), denoting the number of test cases.

For each test case:

Input one line containing two integers p,q(1≤p,q≤107), denoting the given fraction.

Output
For each test case:

If solution exists, output one line containing two integers a,b(1≤a,b≤109), or print two zeros in one line if no solution.

Example
inputCopy
2
5 2
5 1
outputCopy
1 2
0 0
Note
For the first case, 52=12+21 holds. So one possible solution is a=1,b=2.

题意：

给出p/q, 判断是否存在a, b（<1e9），满足 $\frac{p}{q} = \frac{a}{b}+\frac{b}{a}$ 。
如果有，就输出a和b。

思路：

求根公式做法：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

int main(){
    int T;  cin>>T;
    while(T--){
        LL p, q;  cin>>p>>q;
        LL t = p*p-4*q*q;
        if(t < 0 || (LL)sqrt(t)*sqrt(t) != t)cout<<"0 0\n";
        else cout<<(p+(LL)sqrt(t))<<" "<<2*q<<"\n";
    }
    return 0;
}

G.Edge Groups

G. Edge Groups
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Given an undirected connected graph of n vertices and n−1 edges, where n is guaranteed to be odd. You want to divide all the n−1 edges to n−12 groups under following constraints:

There are exactly 2 edges in each group
The 2 edges in the same group share a common vertex
Determine the number of valid dividing schemes modulo 998244353. Two schemes are considered different if there are 2 edges that are in the same group in one scheme but not in the same group in the other scheme.

Input
The first line contains one integer n(3≤n≤105), denoting the number of vertices.

Following n−1 lines each contains two integers u,v(1≤u<v≤n), denoting that vertex u,v are undirectedly connected by an edge.

It is guaranteed that n is odd and that the given graph is connected.

Output
Output one line containing one integer, denoting the number of valid dividing schemes modulo 998244353.

Example
inputCopy
7
1 2
1 3
1 7
4 7
5 7
6 7
outputCopy
3
Note
The 3 schemes are:

The 3 edge groups are {1↔2,1↔3},{1↔7,4↔7},{5↔7,6↔7}
The 3 edge groups are {1↔2,1↔3},{1↔7,5↔7},{4↔7,6↔7}
The 3 edge groups are {1↔2,1↔3},{1↔7,6↔7},{4↔7,5↔7}

题意：

给出一棵树，点数n（1e5）为奇数。
现在将n-1条边分成(n-1)/2组，满足一组只有两条边且有公共点，求满足条件的方案数。

思路：

树上计数dp，令dp[i]表示i的子树所有边全部分解的方案数，最终答案就是dp[1]。
对于转移，有以下转移方程。（参考官方题解，证明）

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N = 2e5+10, mod = 998244353;

vector<int>G[N];
LL dp[N];
int dfs(int u, int f){
    dp[u] = 1;
    int cc = 0;
    for(int to : G[u]){
        if(to==f)continue;
        if(!dfs(to, u))cc++;
        dp[u] = dp[u]*dp[to]%mod;
    }
    for(LL i = 1; i <= cc; i+=2)dp[u]=dp[u]*i%mod;
    return cc&1;  //返回此树的可用边数是否为奇数
}

int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n;  cin>>n;
    for(int i = 1; i < n; i++){
        int u, v;  cin>>u>>v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    dfs(1,-1);
    cout<<dp[1]<<"\n";
    return 0;
}

I.Steadily Growing Steam

I. Steadily Growing Steam
time limit per test1 second
memory limit per test512 megabytes
inputstandard input
outputstandard output

Alice enjoys playing a card game called Steadily Growing Steam (as known as SGS).

In this game, each player will play different roles and have different skills. Players get cards from the deck and use them to play the game. Each card has a numeric label ti, the point number. In addition, each card has a value vi.

Now Alice is playing this game with Bob. According to the skill of Alice’s role, she can have Bob display n cards from the top of the deck. After that, Bob must choose some cards from the n cards and split the chosen cards into two sets that the sum of the cards’ point numbers in the two sets are equal. In other words, if one of the sets is S and another is T , S∩T=∅ and ∑i∈Sti=∑j∈Ttj (Note that S∪T={1,2,⋯n} is not necessary). Then, Alice gets all of the cards in set S and Bob gets the cards in set T.

However, according to the skill of Bob’s role, before choosing the two sets, he can choose at most k different cards and double their point numbers. In other words, he can choose a sequence {a1,a2,⋯,ar},(1≤a1<a2<⋯<ar≤n,0≤r≤k) and for each i(1≤i≤r) , change tai into 2tai. After that he can continue choosing the two sets.

Alice and Bob are partners in this game. Now given the n cards from the deck, they want to know the maximum possible sum of the values of the cards they finally get. In other words, determine the maximum ∑i∈S∪Tvi among all valid schemes(choose cards to double their point numbers, then choose cards and split them into two sets S,T of the same point number sum) and output it.

Input
The first line contains two integers n(1≤n≤100) and k(0≤k≤n), denoting the number of the displayed cards and the maximum number of cards that Bob can choose to double their point numbers, respectively.

The i+1 line contains two integers vi(|vi|≤109) and ti(1≤ti≤13), denoting the value and the point number of the i-th card, respectively.

Output
Output one line containing one integer, denoting the maximum sum of the value of the cards that Alice or Bob can get.

Example
inputCopy
4 1
10 1
-5 3
5 1
6 1
outputCopy
21
Note
One possible scheme:

Double t1 and choose that S={1},T={3,4}, where the point number sum are both 2, and the sum of the card values is 10+5+6=21.

题意：

n个物品（<100），每个物品都有一个价值v和体积t。
现在从中选出至多k个物品，将其体积翻倍，然后将选出的物品分为体积和相等的两堆。
问选出的物品的价值和最大是多少。

思路：

令dp[i, j, k] 表示从前i个物品中，选出j个翻倍，集合1与集合2的体积之差为k时的价值最大值。最终的答案为dp[n,k,0]。
状态转移：
1、不选第i个物品。
2、把第i个物品放入集合1，不翻倍
3、把第i个物品放入集合2，不翻倍
4、把第i个物品放入集合1，翻倍
5、把第i个物品放入集合2，翻倍
其中k作差后的取值为可能为负数，所以都+3000，映射到正数范围即可。
数组不够开，所以用滚动数组优化。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, M = 7000;
int v[N], t[N]; //价值，体积
LL f[2][N][M];  //前i个物品中，选出j个翻倍，两集合体积差为k
int main(){
    int n, m;  cin>>n>>m;
    for(int i = 1; i <= n; i++)cin>>v[i]>>t[i];
    memset(f, 0xc0, sizeof(f));
    for(int i = 0; i <= m; i++)f[0][i][3000] = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 0; j <= m; j++){
            for(int k = 0; k <= 6000; k++){
                //不选i, 放1不翻倍, 放2不翻倍, 放1翻倍, 放2翻倍
                int x = i&1;
                f[x][j][k] = f[x^1][j][k];
                if(k-t[i]>=0) f[x][j][k]=max(f[x][j][k],f[x^1][j][k-t[i]]+v[i]);
				if(k+t[i]<=6000) f[x][j][k]=max(f[x][j][k],f[x^1][j][k+t[i]]+v[i]);
				if(j!=0){
					if(k-2*t[i]>=0)f[x][j][k]=max(f[x][j][k],f[x^1][j-1][k-2*t[i]]+v[i]);
					if(k+2*t[i]<=6000)f[x][j][k]=max(f[x][j][k],f[x^1][j-1][k+2*t[i]]+v[i]);
				}
            }
        }
    }
    cout<<f[n&1][m][3000]<<"\n";
    return 0;
}

H.Life is a Game

H. Life is a Game
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Life is a game.

The world can be regarded as an undirected connected graph of n cities and m undirected roads between the cities. Now you, the life game player, are going to play the life game on the world graph.

Initially, you are at the x-th city and of k social ability points. You can earn social ability points by living and working. Specifically, you can earn ai social ability points by living and working in the i-th city. But in this problem, you cannot earn social ability points duplicatedly in one city, so you want to travel the world and earn more social ability points. However, the roads are not easy. Specifically, there is an ability threshold wi for the i-th road, you should be of at least wi social ability points to go through the road. Moreover, Your social ability point will not decrease when passing roads but just need to be at least wi if you want to go through the i-th road.

So as you can see, the life game is just living, working and traveling repeatedly. There are q game saves. For each game save, the initial city and social ability point is given and the player has not lived or worked in any city. Now you, the real life game player, need to determine the maximum possible number of social ability points you can have in the end of the game and output it for each given game save.

Input
The first line contains three integers n,m,q(1≤n,m,q≤105), denoting the number of cities, roads and game saves respectively.

The second line contains n integers a1,a2,⋯,an(1≤ai≤104), denoting the bonus social ability points for the cities.

Following m lines each contains three integers u,v,w(1≤u<v≤n,1≤w≤109), denoting that cities u,v are undirectedly connected by a road of ability threshold w.

Following q lines each contains two integers x,k(1≤x≤n,1≤k≤109), denoting the game saves.

Output
For each game save, output one line containing one integer, denoting the maximum possible number of social ability points you can have.

Example
inputCopy
8 10 2
3 1 4 1 5 9 2 6
1 2 7
1 3 11
2 3 13
3 4 1
3 6 31415926
4 5 27182818
5 6 1
5 7 23333
5 8 55555
7 8 37
1 7
8 30
outputCopy
16
36
Note
Following is a illustration of the given graph.

For the first game save, you can reach 4 cities {1,2,3,4} and have 7+3+1+4+1=16 social ability points in the end
For the second game save, you can only reach the initial city {8} and have 30+6=36 social ability points in the end

题意：

一张无向连通图，每个点有声望vi，第一次经过一个点可以得到这个声望。每条边有一个限制wi，要想经过这条边需要身上的声望大于等于wi。
现给出q次询问，每次给出一个起始点x和初始身上拥有的声望k，问最多能获得多少声望。

思路：

在初始位置时，每次贪心的走与自己已经走过的连通块相连的wi最小的边肯定更优，即尽可能让生成树中的最大边权最小（瓶颈生成树，区别于最小生成树的边权和最小，不过最小生成树本身也都是瓶颈生成树，充分不必要条件）。
当你在经过一条边权暂时最大的边后，与你经过的连通块相连的所有比这条边小的边都可以走从而获得可以经过的点的价值。
Kruskal重构树是一个类似于最小生成树的东西，但是建出来的树有2n-1个节点，这个树的叶子节点都是1到n的原图节点，而重构树新建的非叶节点的点权值就是之前的边权。
Kruskal重构树适用于求一个无向图，然后给你个点，让你在只能经过边权大于等于x的边（边有个限制），求能到达的顶点的一些性质（个数，权值最大等等）。。
假设我从1出发，只能经过边权小于等于3的边，那么我就在1的父亲节点里找最后一个小于等于3的边即可(因为这是一个大根堆)，然后找到了这个父节点假设为fa，那么fa的子树上的叶子节点都是从1满足限制条件能到达的节点。
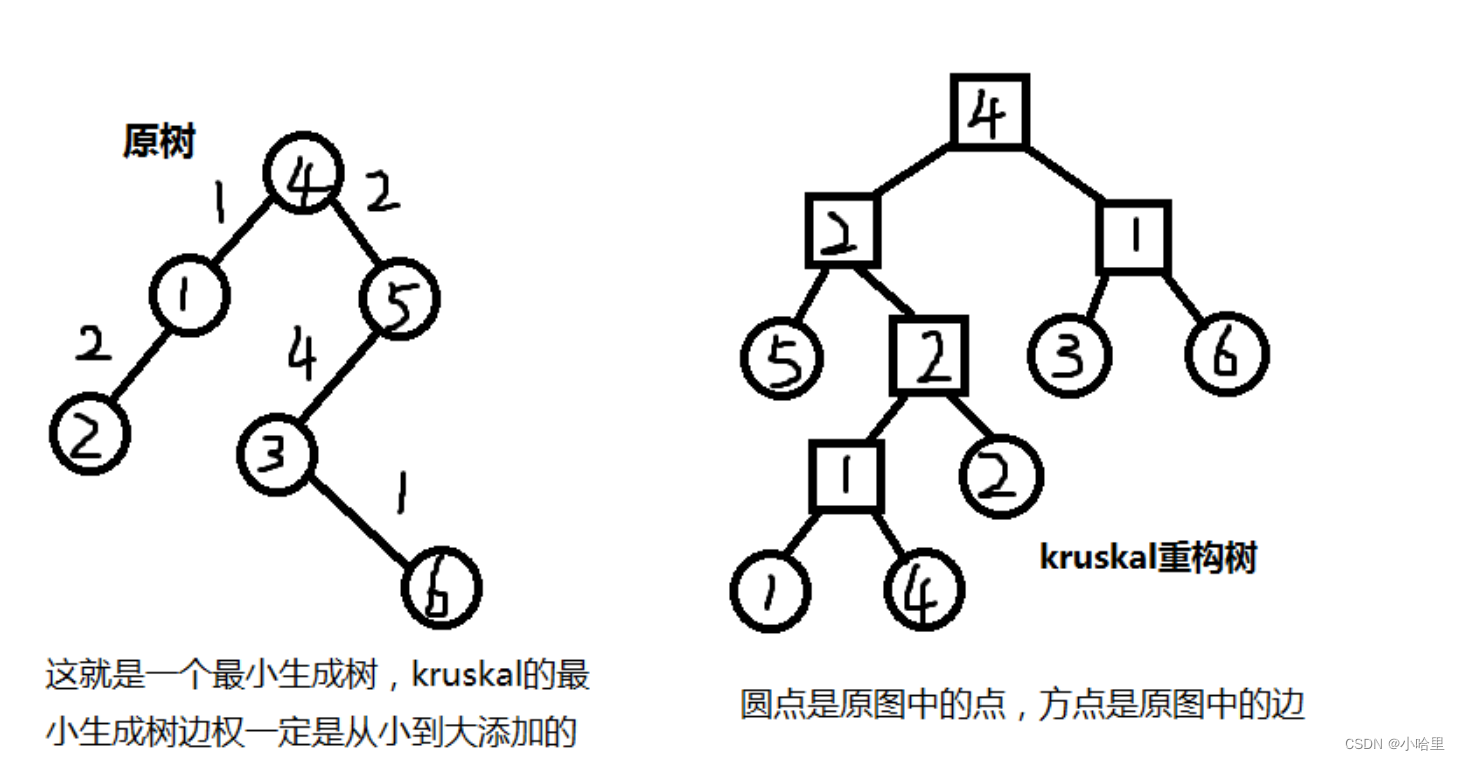
此时原题就变成了一个模板题，对原题建Kruskal重构树。
那么我们对于某个询问，只需要从对应的叶节点开始往上跳到祖先节点（倍增加速跳），直至跳不过去（即这条边下面的子树的叶子点权和加上初始声望值小于该边边权）。
把下面子树的叶子点权和加上初始声望，即为答案。

#include<bits/stdc++.h>
using namespace std;
const int N = 4e5+10;

struct edge{ int u, v, w; }e[N];
bool cmp(edge x, edge y){ return x.w<y.w; }
int a[N];
int pre[N][20], ne[N][20];

int fa[N+10];
void init(int n){for(int i = 0; i <= n; i++)fa[i]=i;}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void merge(int x, int y){x=find(x);y=find(y);if(x!=y)fa[x]=y;}

int main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, m, q;  cin>>n>>m>>q;
    for(int i = 1; i <= n; i++)cin>>a[i];
    for(int i = 1; i <= m; i++)cin>>e[i].u>>e[i].v>>e[i].w;
    //创建Kruskal重构树
    sort(e+1,e+m+1, cmp);
    init(n*2);
    int nn = n;
    for(int i = 1; i <= m; i++){
        int x = find(e[i].u), y = find(e[i].v);
        if(x != y){
            fa[x] = fa[y] = ++nn;
            a[nn] = a[x]+a[y];    //新建边节点
            pre[x][0] = pre[y][0] = nn;
            ne[x][0] = e[i].w-a[x];
            ne[y][0] = e[i].w-a[y];
        }
    }
    a[0] = a[nn];
    //预处理倍增
    for(int i = nn; i >= 1; i--){
        for(int j = 1; j < 19; j++){
            pre[i][j] = pre[pre[i][j-1]][j-1];
            ne[i][j] = max(ne[i][j-1], ne[pre[i][j-1]][j-1]);
        }
    }
    //solve
    while(q--){
        int x, k;  cin>>x>>k;
        for(int p = 18; p >= 0; p--){
            if(ne[x][p]<=k)x = pre[x][p];
        }
        cout<<a[x]+k<<"\n";
    }
    return 0;
}

K.Circle of Life

K. Circle of Life
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Your friend Lucky is a little elf. Recently, Lucky discovered a magical creature, she named them “Twinkle”. Lucky has a magical chain of n vertices and n−1 edges, where the vertices are connected by the edges one by one. We assume that the vertices are numbered 1 to n from left to right, and the i-th edge connects vertex i and vertex i+1. She found that Twinkles could live in the magical chain.

Lucky can put some Twinkles on some vertices simultaneously with her magic, but there should be at most one Twinkle in one vertex since the near Twinkles will perish together. Then, every second, each Twinkle will split into two Twinkles simultaneously and they will dash in the opposite directions to the two adjacent vertices.

Formally, a Twinkle in vertex u splits into two Twinkles, the left splited Twinkle and the right splited Twinkle.

The left splited Twinkle will dash toward the left and reach the vertex u−1.
The right splited Twinkle will dash toward the right and reach the vertex u+1.
But unluckily, if one side has no vertex, the Twinkle will dash out of the chain and die out(for the left splited Twinkle in vertex 1 and the right splited Twinkle in vertex n). Much more unfortunately, if two Twinkles dash to have a head-on collision (i.e. meet in the same vertex or edge), they will perish together with a tearing crash! Specifically, a crash will happen in two situations:

The right splited Twinkle in vertex i and the left splited Twinkle in vertex i+2 will crash in vertex i+1(assuming that vertex i+1 lives no Twinkle).
The right splited Twinkle in vertex i and the left splited Twinkle in vertex i+1 will crash in the i-th edge.
Lucky hopes there’s always some Twinkle living on the chain. In addition, in order to be more convenient for Lucky to check the validity, there should be duplicated configurations within 2n seconds. Specifically, a configuration can be denoted by a binary string S of length n, where Si=1 iff vertex i lives a Twinkle, and Ci denotes the configuration after i seconds. Your task is to find an initial configuration C0 so that for each i(0≤i≤2n),Ci≠00⋯00 and that there exist two integers i,j(0≤i<j≤2n),Ci=Cj.

Input
Input one line containing one integer n(2≤n≤123), denoting the length of the chain.

Output
If there is no solution, just output “Unlucky”(without quotes) in one line.

Otherwise, output one line containing one binary string, denoting the initial configuration you found.

Examples
inputCopy
2
outputCopy
10
inputCopy
4
outputCopy
1000
Note
For the first case, the configurations will change like this:
10→01→10
, where C0=C2 holds.

For the second case, the configurations will change like this:
1000→0100→1010→0001→0010→0101→1000
, where C0=C6 holds.

题意：

游戏规则：
1、从左到右，有n个节点由n-1条边相连，节点编号分别1-n。初始状态由一个长度为n的01串S给出，S[i]=1表示节点i处有精灵，反之没有，每个节点处最多只有一个精灵。
2、现进行2n次变换，每次变换时所有精灵会同时分裂成两个精灵，其中一个精灵向左移动，另一个精灵向右移动。当两个精灵在节点处或边上相遇时会湮灭。（在节点1处向左移动、在节点n处向右移动的精灵会湮灭）
题目给你n，要求构造一个开始局面，使得能在规则下迭代 2n 次以内就产生循环，并且循环不能是全0的局面（至少保留一个精灵）。

思路：

根据样例的n=2和4，容易猜想n为偶数时都可以构造0110011001（01后面接10，10后面接01即可），这样字符串只要2秒就可以产生循环。
对于n为奇数时，构造010+偶数部分（偶数部分用10开头）。
这样在第一秒时，字符串会变为：100(第3位会与偶数部分开头的1相撞，因此还是为0)+偶数部分。第二秒：010+偶数部分（第二秒即可成功复原）
参考题解：参考1，参考2

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n;  cin>>n;
    if(n==1 || n==3){ cout<<"Unlucky\n"; return 0; }
    if(n%2){ cout<<"010";  n-= 3; }
    n >>= 1;
    for(int i = 0; i < n; i++){
        if(i%2)cout<<"01";else cout<<"10";
    }
    return 0;
}