描述

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。

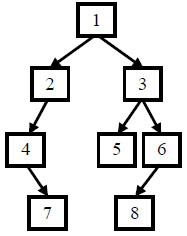
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

提示:

1.vin.length == pre.length

2.pre 和 vin 均无重复元素

3.vin出现的元素均出现在 pre里

4.只需要返回根结点，系统会自动输出整颗树做答案对比

数据范围： n ≤ 2000，节点的值 −10000 ≤ val ≤ 10000

要求：空间复杂度 O(n)，时间复杂度 O(n)

示例1

输入：

[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]

返回值：

{1,2,3,4,#,5,6,#,7,#,#,8}

说明：

返回根节点，系统会输出整颗二叉树对比结果，重建结果如题面图示   

示例2

输入：

[1],[1]

返回值：

{1}

示例3

输入：

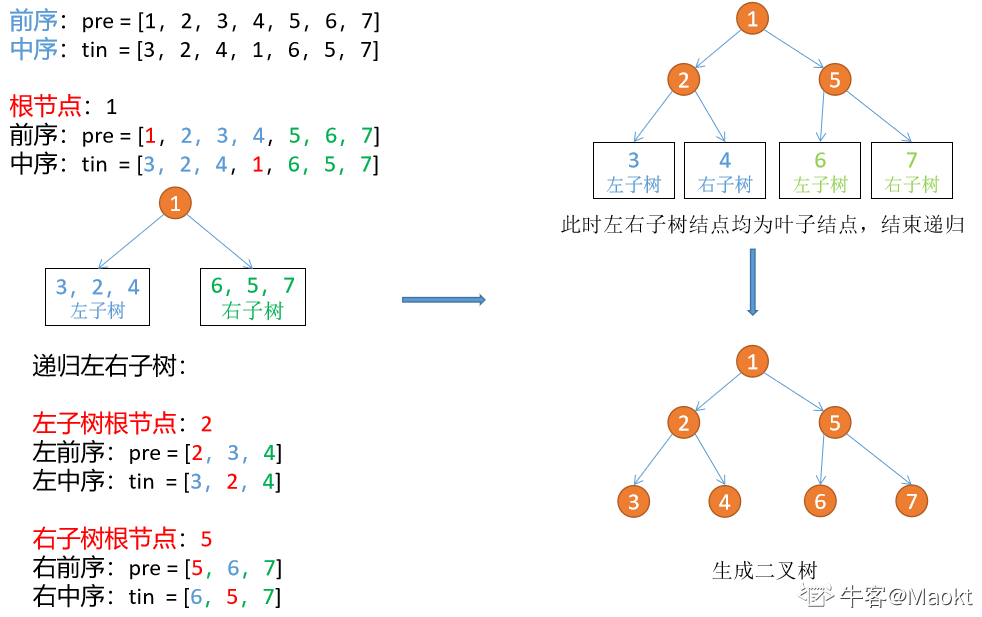
[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]

返回值：

{1,2,5,3,4,6,7}

使用前序和中序，完成二叉树的重建。

解决方法：

1、前序的第一个数字A，即为当前分支的根节点

2、在中序中找到 A，并将数组划分为两部分，左边的为 A 的左树节点，右边为 A 的右树节点

3、重复12过程，直到数组边界

    public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
        if (pre == null || vin == null || pre.length != vin.length || pre.length == 0) {
            return null;
        }
        return buildSubTree(pre, vin, 0, pre.length);
    }

    int prePos = 0;

    public TreeNode buildSubTree(int[] pre, int[] vin, int start, int end) {
        int length = end - start;
        if (length <= 0) {
            return null;
        }
        int preValue = pre[prePos++];
        TreeNode node = new TreeNode(preValue);
        if (length == 1) {
            return node;
        }
        int vinPos;
        for (vinPos = start; vinPos < end; vinPos++) {
            if (vin[vinPos] == preValue) {
                break;
            }
        }
        node.left = buildSubTree(pre, vin, start, vinPos);
        node.right = buildSubTree(pre, vin, vinPos + 1, end);
        return node;
    }