TCP 拥塞控制目标是缓解并解除网络拥塞,让所有流量公平共享带宽,合在一起就是公平收敛。
AIMD(几乎所有与拥塞控制相关的协议或算法都有 AIMD 的影子,包括 RoCE,BBRv2) 为什么收敛?我一般会给出下面的老图:
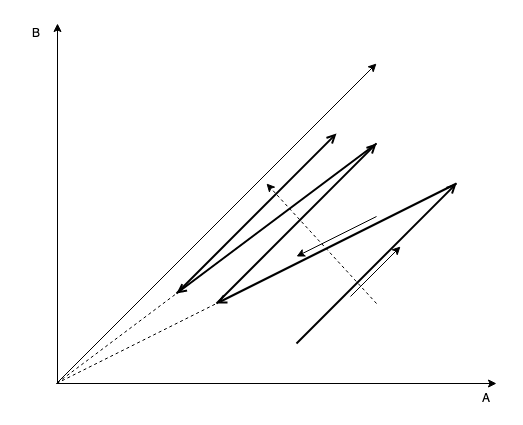
虽然只展示了两条流的收敛,但 n 条流收敛的展示无非就是将 2 维坐标系换成 n 维坐标系,只要能证明任意的 2 维截面都如上图所示就行,而这件事简单推导一下就行,比画坐标系还要直观,再说超过 3 维的坐标系也画不出来。
设一个 AIMD 系统的 AIMD 参数为 α \alpha α, β \beta β, w i 0 w_{i0} wi0 和 w j 0 w_{j0} wj0 分别为任意两条流的初始窗口,且 w i 0 > w j 0 w_{i0}>w_{j0} wi0>wj0,二者之差 d 0 = W i 0 − W j 0 d_0=W_{i0}-W_{j0} d0=Wi0−Wj0。
假设所有流同步(异步流和 RED 作用下相对复杂,用统计分布代替公式),一个 AIMD 周期后,两条流的 cwnd 分别为 w i 0 = w i = β ∗ ( w i 0 + α ) w_{i0}=w_i= \beta*(w_{i0}+\alpha) wi0=wi=β∗(wi0+α) 和 w j 0 = w j = β ∗ ( w j 0 + α ) w_{j0}=w_j= \beta*(w_{j0}+\alpha) wj0=wj=β∗(wj0+α),此时两条流 cwnd 之差 d = β ∗ d 0 d=\beta*d_0 d=β∗d0。
再下一个周期, w i 0 = w i = β ∗ ( β ∗ ( w i 0 + α ) + α ) w_{i0}=w_i= \beta*(\beta*(w_{i0}+\alpha)+\alpha) wi0=wi=β∗(β∗(wi0+α)+α) 和 w j 0 = w j = β ∗ ( β ∗ ( w j 0 + α ) + α ) w_{j0}=w_j= \beta*(\beta*(w_{j0}+\alpha)+\alpha) wj0=wj=β∗(β∗(wj0+α)+α),两条流 cwnd 之差 d = β 2 ∗ d 0 d=\beta^2*d_0 d=β2∗d0。
容易得到,在第 n 个 AIMD 周期后,两条流 cwnd 之差为 d = β n d 0 d=\beta^nd_0 d=βnd0,趋向于 0,这意味着无论初始时刻任意两条流差异多么大,最终它们将趋同。
值得注意的是,无论是 AI 过程还是 MD 过程,都单独对收敛有贡献,假设持续 AI,从不 MD,观察一个比值 w i 0 + x w j 0 + x \dfrac{w_{i0}+x}{w_{j0}+x} wj0+xwi0+x, x 越大,比值越趋向于 1,在总体量面前,差异将无关紧要,另一方面,假设持续 MD,从不 AI,观察一个差值 β x ∗ w i 0 − β x ∗ w j 0 \beta^x*w_{i0}-\beta^x*w_{j0} βx∗wi0−βx∗wj0, x 越大,该差值趋向于 0,宏观上看,差异消失。
总体而言,AI 的过程与初始值无关,它是一种与初始优势相反的力量,保持差值不变,比例趋向公平,削减掉相对差异,而 MD 则与初始值强相关,但它下降的速率越来越慢,保持差值趋向公平,比例不变,削减掉绝对差异。AIMD 共同作用,各自效用独立积累,无论在比例差异还是在绝对差异均被时间抹平。
举个例子,A 有 1 块钱,B 有 9 块钱,两人很公平,因为购买力有绝对值下限,虽然 A 和 B 相差 9 倍,但他们可能都买不到东西,但 A 有 100 万块,B 有 900 万块,就不再公平了,此时 9 倍的差异关乎他们生活在不同层次,如果 A 有 1 亿零 100 块,B 有 1 亿零 900 块,又会非常公平。
大概社会平均工资,普调,年终奖,股权被稀释,工资被倒挂,就和 AIMD,AIAD,MIMD,MIAD 有关。用上述的简单推导可以证明,除了 AIMD 可以收敛到公平,其它 3 种均不行。
AIMD-based cc,比如 reno,cubic,scalable,highspeed,它们被认为不如 BBR,但事后看,这些算法并不是在根本上不如 BBR,而 BBR 也不是根本上就优秀,前面说过,BBR 的高效来自于瞬时记住并憋住的 maxbw,而 cubic(包括其它 AIMD cc) 的问题在于它不能识别随机丢包。而 AIMD 本身与效率无关,它只关注公平收敛。
cubic 只要增加丢包分类识别就能解决问题, 而 BBR 无论 probebw 还是 probertt 均无法完备论证收敛,只在 “效果” 上显示出 “加速比与带宽占比负相关”,而这是过不了审的。
已经有了很多 “cubic-改” 算法,大多数引入了 delay 甚至 delay 梯度,在丢包发生时二次确认拥塞是否真实存在,事实上 westwood 就是一种比较合理的算法,它收敛到瓶颈带宽,而不是固定比例。然而由于实现粗糙(依然是受制于 Linux 拥塞状态机),westwood 未竟全功。
还有另一种拥塞判定方法,二次机会法,事先为 AIMD 准备两个 beta 参数,当检测到丢包时,随即将 cwnd 下降一个更小的 beta 比例,进入包守恒开始重传恢复,如果重传率超过一个阈值,则将 cwnd 下降更大的 beta,视情况从两个 MD 中任意一个开始进行 AI:
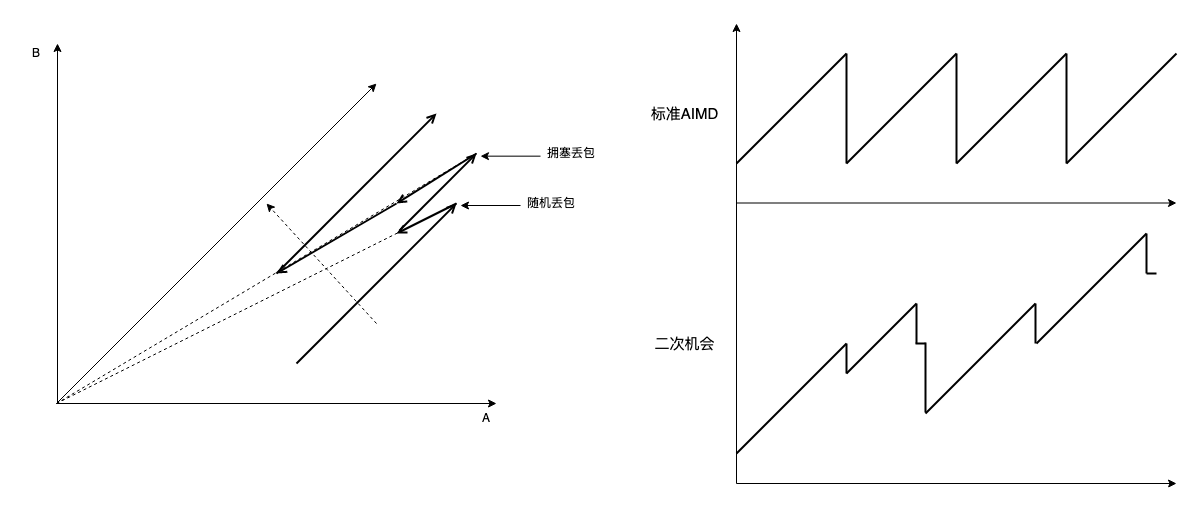
避开的只是随机丢包,丝毫不影响拥塞丢包后的收敛。
非常简单,不需要像 westwood 还要计算瓶颈带宽,代价就是误判会增加重传率,好在只有二次机会,只会增加一点点,不像 BBR 憋住 10 round 那样执着。
公平收敛,抓住一个小基本点就行了,这是控制平面的底座,其它的,留给应用自己以及底层链路,就好像线路断了,再好的算法也无济于事,另一方面,application-limited 传输,再好的算法也用不上,但无论如何,公平是刚需。
其实菜市场摊贩就遵循 AIMD 以避开相互内耗的价格战,最终你会发现各个摊贩的菜价都一样,差别只是质量口碑而已。菜市场刚开张时,各家促销,缓慢加价,最终发现客户流失时,又大减价(注意这个 “大” 字),大促销,最终他们的价格趋向于一致。当然,TCP 这方面属于后生,但 AIMD 是一个放之四海而皆准的通用控制论模型,在它的框架下做事就对了,但凡违背的,事情将会越发精细,复杂。
浙江温州皮鞋湿,下雨进水不会胖。