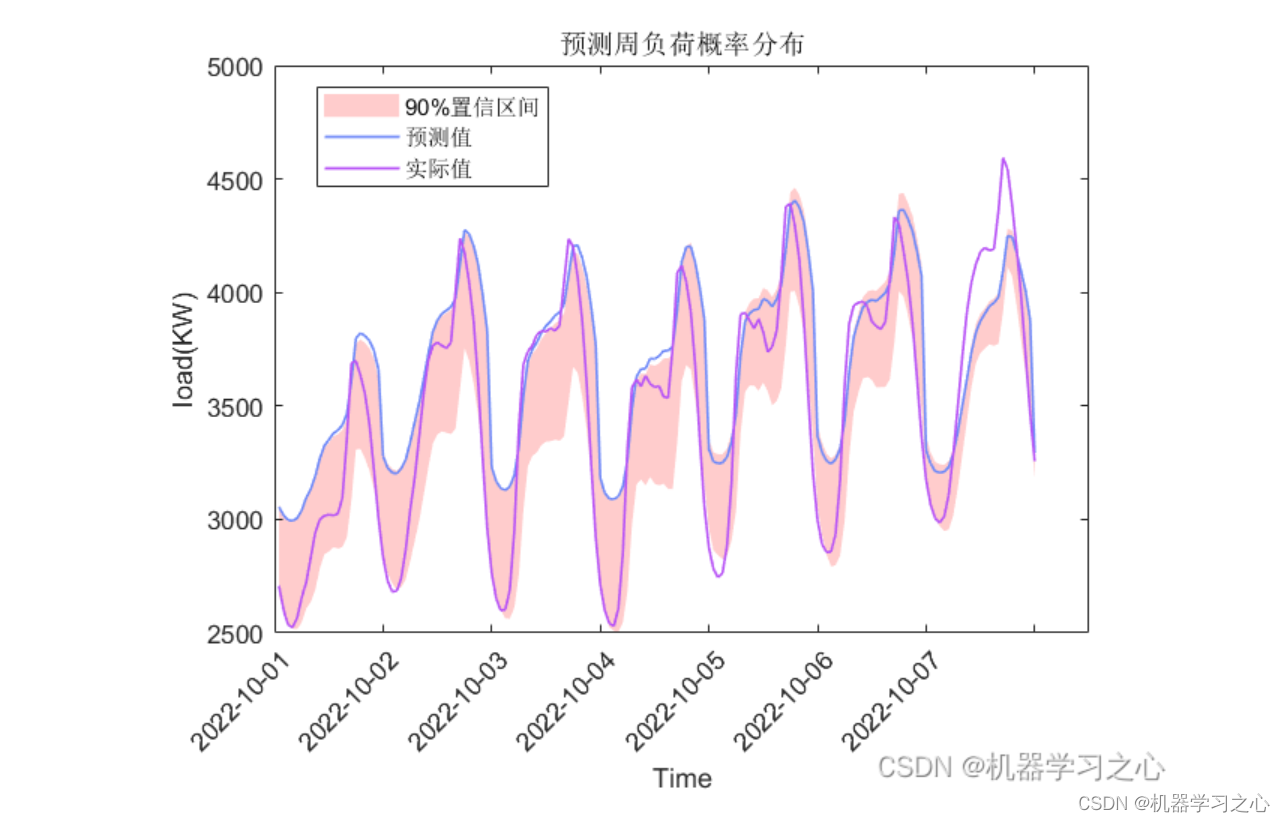
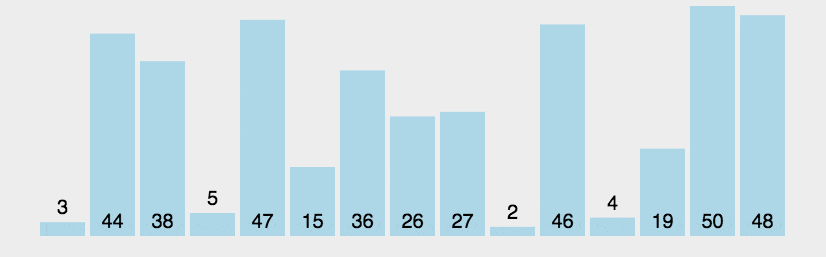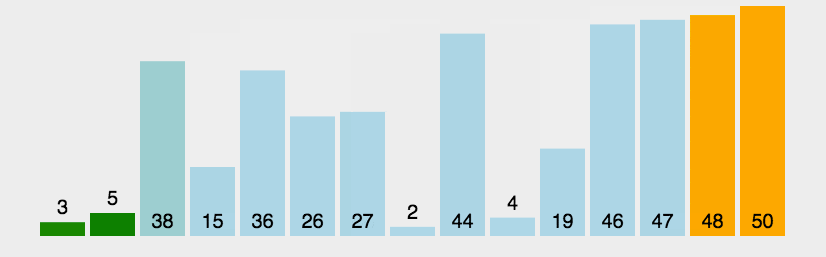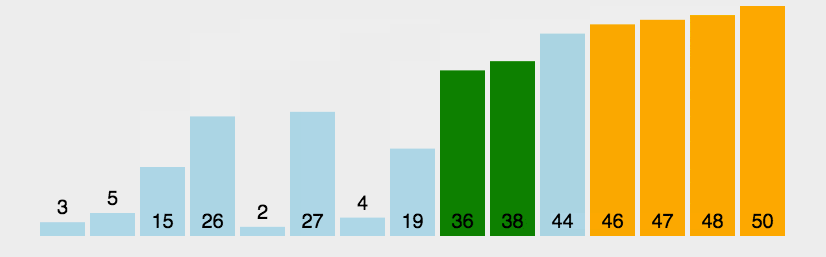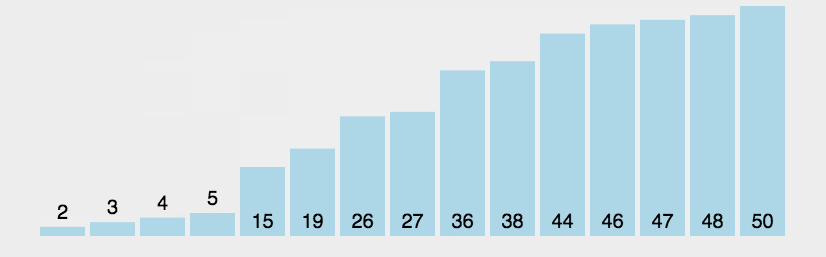OpenCV实战——根据立体图像计算深度信息
- 0. 前言
- 1. 立体视觉系统
- 2. 计算深度信息
- 3. 完整代码
- 相关链接
0. 前言
人类可以用两只眼睛构建三个维度世界,而为机器人配备两个摄像头时,机器人同样也可以做到这一点,这称为立体视觉 (stereo vision)。安装在设备上的一对摄像机可以观察同一场景并由固定基线(即两个摄像机之间的距离)分隔。本节将介绍如何通过计算两个视图之间的深度对应关系根据两个立体图像计算深度图像。
1. 立体视觉系统
立体视觉系统通常由两个并排且朝向相同的相机组成,下图展示了这种立体视觉系统:

在这种理想配置下,相机仅在水平方向平移,因此所有极线都是水平的。这意味着对应点具有相同的
y
y
y 坐标,从而减少了在一维度上的匹配搜索。
x
x
x 坐标的差异取决于点的深度,无穷远处的点在图像中具有相同的坐标
(
x
,
y
)
(x,y)
(x,y),且这些点离立体视觉装置越近,它们的
x
x
x 坐标差异就越大,这可以由投影方程证明。当相机仅在水平方向移动时,第二个相机的投影方程如下:
S
[
x
′
y
′
1
]
=
[
f
0
u
0
0
f
v
0
0
0
1
]
[
1
0
0
−
B
0
1
0
0
0
0
1
0
]
[
X
Y
Z
1
]
S\left[ \begin{array}{ccc} x'\\ y'\\ 1\\\end{array}\right]=\left[ \begin{array}{ccc} f&0&u_0\\ 0&f&v_0\\ 0&0&1\\\end{array}\right]\left[ \begin{array}{ccc} 1&0&0&-B\\ 0&1&0&0\\ 0&0&1&0\\\end{array}\right]\left[ \begin{array}{ccc} X\\ Y\\ Z\\ 1\\\end{array}\right]
S
x′y′1
=
f000f0u0v01
100010001−B00
XYZ1
为了简单起见,我们假设两个相机具有相同的方形像素和校准参数。如果计算
x
−
x
′
x-x'
x−x′ 的差值(除以
s
s
s 以标准化齐次坐标)并忽略
z
z
z 坐标,可以得到以下等式:
Z
=
f
(
x
−
x
′
)
B
Z=f\frac {(x-x')} {B}
Z=fB(x−x′)
其中,
(
x
−
x
′
)
(x-x')
(x−x′) 称为视差 (disparity)。为了计算立体视觉系统的深度图,必须估计每个像素的视差。本节,将介绍如何计算视差。
2. 计算深度信息
上一小节中展示的理想模型在现实中很难实现。即使它们可以准确定位,立体装置的摄像机也不可避免地会包含一些额外的平移和旋转。但我们可以对图像进行校正以产生水平线,可以通过使用鲁棒匹配算法来计算立体系统的基本矩阵来实现。例如,在以下图像上绘制核线:

OpenCV 提供了一个整流函数,它使用单应变换将每个相机的图像平面投影到完美对齐的虚拟平面上。
(1) 单应变换根据一组匹配点和一个基本矩阵进行计算。计算完成后,将在图像中应用这些单应性:
// 计算同形校正
cv::Mat h1, h2;
cv::stereoRectifyUncalibrated(points1, points2, fundamental, image1.size(), h1, h2);
// 通过扭曲矫正图像
cv::Mat rectified1;
cv::warpPerspective(image1, rectified1, h1, image1.size());
cv::Mat rectified2;
cv::warpPerspective(image2, rectified2, h2, image1.size());
对于示例图像,校正后的图像对如下所示:

(2) 可以通过假设相机平行以及水平极线来计算视差图:
// 差异计算
cv::Mat disparity;
cv::Ptr<cv::StereoMatcher> pStereo = cv::StereoSGBM::create(0, // 最小差异
32, // 最大差异
5); // 块大小
pStereo->compute(rectified1, rectified2, disparity);
(3) 可以将获得的视差图显示为图像。明亮的值表示高视差,高视差值对应于近端对象:

计算视差的质量主要取决于组成场景的不同对象,高纹理区域往往会产生更准确的视差估计,因为它们可以无歧义地匹配。此外,较大的基线会增加可检测深度值的范围,但扩大基线也会使视差计算更加复杂和不可靠。
当图像被正确校正后,搜索空间就可以与图像对齐。然而,在立体视觉中,我们通常需要密集的视差图。也就是说,我们希望将一幅图像的每个像素与另一幅图像的像素进行匹配。这比在一张图像中选择几个不同的点并在另一张图像中找到它们的对应点更具挑战性。因此,视差计算是一个复杂的过程,通常由四步组成:
- 匹配误差计算
- 误差汇总
- 视差计算和优化
- 视差改进
为一个像素分配视差是将一对点对应放入立体集合中,寻找最佳视差图通常是一个优化问题。从这个角度来看,匹配两个点的误差必须按照定义的度量进行计算,例如,可以是强度、颜色或梯度的绝对或平方差。在寻找最优解的过程中,匹配误差通常在一个区域上聚合,以应对局部噪声的影响。然后可以通过评估能量函数来估计全局视差图,该能量函数平滑视差图项,考虑可能的遮挡并强制执行唯一性约束。最后,通常应用后处理步骤以优化视差估计,例如检测平面区域或检测深度不连续性。
OpenCV 实现了许多视差计算方法,本节我们使用 cv::StereoSGBM 方法。最简单的方法是基于块匹配的 cv::StereoBM 函数。
最后,如果结合 cv::stereoCalibrate 和 cv::stereoRectify 函数进行完整的校准过程,则可以执行更准确的校正。然后,整流映射为相机计算新的投影矩阵,而非简单的单应性。
3. 完整代码
头文件 (robustMatcher.h) 完整代码参考基于随机样本一致匹配图像一节,主函数文件 (stereoMatcher.cpp) 完整代码如下所示:
#include <iostream>
#include <vector>
#include <numeric>
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <opencv2/objdetect/objdetect.hpp>
#include <opencv2/xfeatures2d.hpp>
#include <opencv2/viz.hpp>
#include "robustMatcher.h"
int main() {
// 读取输入图像
cv::Mat image1= cv::imread("1.png",0);
cv::Mat image2= cv::imread("2.png",0);
if (!image1.data || !image2.data)
return 0;
// SIFT 检测器和匹配器
RobustMatcher rmatcher(cv::xfeatures2d::SIFT::create(250));
// 匹配两张图像
std::vector<cv::DMatch> matches;
std::vector<cv::KeyPoint> keypoints1, keypoints2;
cv::Mat fundamental = rmatcher.match(image1, image2, matches,
keypoints1, keypoints2);
// 绘制匹配
cv::Mat imageMatches;
cv::drawMatches(image1, keypoints1, // 第一张图像及其关键点
image2, keypoints2, // 第二张图像及其关键点
matches, // 匹配
imageMatches, // 结果图像
cv::Scalar(255, 255, 255),
cv::Scalar(255, 255, 255),
std::vector<char>(),
cv::DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
cv::namedWindow("Matches");
cv::imshow("Matches", imageMatches);
// 将关键点转换为 Point2f
std::vector<cv::Point2f> points1, points2;
for (std::vector<cv::DMatch>::const_iterator it = matches.begin();
it != matches.end(); ++it) {
float x = keypoints1[it->queryIdx].pt.x;
float y = keypoints1[it->queryIdx].pt.y;
points1.push_back(keypoints1[it->queryIdx].pt);
x = keypoints2[it->trainIdx].pt.x;
y = keypoints2[it->trainIdx].pt.y;
points2.push_back(keypoints2[it->trainIdx].pt);
}
// 计算同形校正
cv::Mat h1, h2;
cv::stereoRectifyUncalibrated(points1, points2, fundamental, image1.size(), h1, h2);
// 通过扭曲矫正图像
cv::Mat rectified1;
cv::warpPerspective(image1, rectified1, h1, image1.size());
cv::Mat rectified2;
cv::warpPerspective(image2, rectified2, h2, image1.size());
cv::namedWindow("Left Rectified Image");
cv::imshow("Left Rectified Image", rectified1);
cv::namedWindow("Right Rectified Image");
cv::imshow("Right Rectified Image", rectified2);
points1.clear();
points2.clear();
for (int i = 20; i < image1.rows - 20; i += 20) {
points1.push_back(cv::Point(image1.cols / 2, i));
points2.push_back(cv::Point(image2.cols / 2, i));
}
// 绘制对极线
std::vector<cv::Vec3f> lines1;
cv::computeCorrespondEpilines(points1, 1, fundamental, lines1);
for (std::vector<cv::Vec3f>::const_iterator it = lines1.begin();
it != lines1.end(); ++it) {
cv::line(image2, cv::Point(0, -(*it)[2] / (*it)[1]),
cv::Point(image2.cols, -((*it)[2] + (*it)[0] * image2.cols) / (*it)[1]),
cv::Scalar(255, 255, 255));
}
std::vector<cv::Vec3f> lines2;
cv::computeCorrespondEpilines(points2, 2, fundamental, lines2);
for (std::vector<cv::Vec3f>::const_iterator it = lines2.begin();
it != lines2.end(); ++it) {
cv::line(image1, cv::Point(0, -(*it)[2] / (*it)[1]),
cv::Point(image1.cols, -((*it)[2] + (*it)[0] * image1.cols) / (*it)[1]),
cv::Scalar(255, 255, 255));
}
cv::namedWindow("Left Epilines");
cv::imshow("Left Epilines", image1);
cv::namedWindow("Right Epilines");
cv::imshow("Right Epilines", image2);
// 绘制匹配
cv::drawMatches(image1, keypoints1,
image2, keypoints2,
std::vector<cv::DMatch>(),
imageMatches,
cv::Scalar(255, 255, 255),
cv::Scalar(255, 255, 255),
std::vector<char>(),
cv::DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
cv::namedWindow("A Stereo pair");
cv::imshow("A Stereo pair", imageMatches);
// 差异计算
cv::Mat disparity;
cv::Ptr<cv::StereoMatcher> pStereo = cv::StereoSGBM::create(0, // 最小差异
32, // 最大差异
5); // 块大小
pStereo->compute(rectified1, rectified2, disparity);
// 绘制整流对
/*
cv::warpPerspective(image1, rectified1, h1, image1.size());
cv::warpPerspective(image2, rectified2, h2, image1.size());
cv::drawMatches(rectified1, keypoints1, // 1st image
rectified2, keypoints2, // 2nd image
std::vector<cv::DMatch>(),
imageMatches, // the image produced
cv::Scalar(255, 255, 255),
cv::Scalar(255, 255, 255),
std::vector<char>(),
2);
cv::namedWindow("Rectified Stereo pair");
cv::imshow("Rectified Stereo pair", imageMatches);
*/
double minv, maxv;
disparity = disparity * 64;
cv::minMaxLoc(disparity, &minv, &maxv);
std::cout << minv << "+" << maxv << std::endl;
cv::namedWindow("Disparity Map");
cv::imshow("Disparity Map", disparity);
cv::waitKey();
return 0;
}
相关链接
OpenCV实战(1)——OpenCV与图像处理基础
OpenCV实战(2)——OpenCV核心数据结构
OpenCV实战(3)——图像感兴趣区域
OpenCV实战(4)——像素操作
OpenCV实战(5)——图像运算详解
OpenCV实战(6)——OpenCV策略设计模式
OpenCV实战(7)——OpenCV色彩空间转换
OpenCV实战(8)——直方图详解
OpenCV实战(9)——基于反向投影直方图检测图像内容
OpenCV实战(10)——积分图像详解
OpenCV实战(11)——形态学变换详解
OpenCV实战(12)——图像滤波详解
OpenCV实战(13)——高通滤波器及其应用
OpenCV实战(14)——图像线条提取
OpenCV实战(15)——轮廓检测详解
OpenCV实战(16)——角点检测详解
OpenCV实战(17)——FAST特征点检测
OpenCV实战(18)——特征匹配
OpenCV实战(19)——特征描述符
OpenCV实战(20)——图像投影关系
OpenCV实战(21)——基于随机样本一致匹配图像
OpenCV实战(22)——单应性及其应用
![[亲测有效] 如何实现vivo图案解锁](https://img-blog.csdnimg.cn/img_convert/e4f44a03a6fed40a8e579144a03d24c2.png)