区间预测 | MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测

效果一览

• 进阶版
  
  
  

• 基础版
  

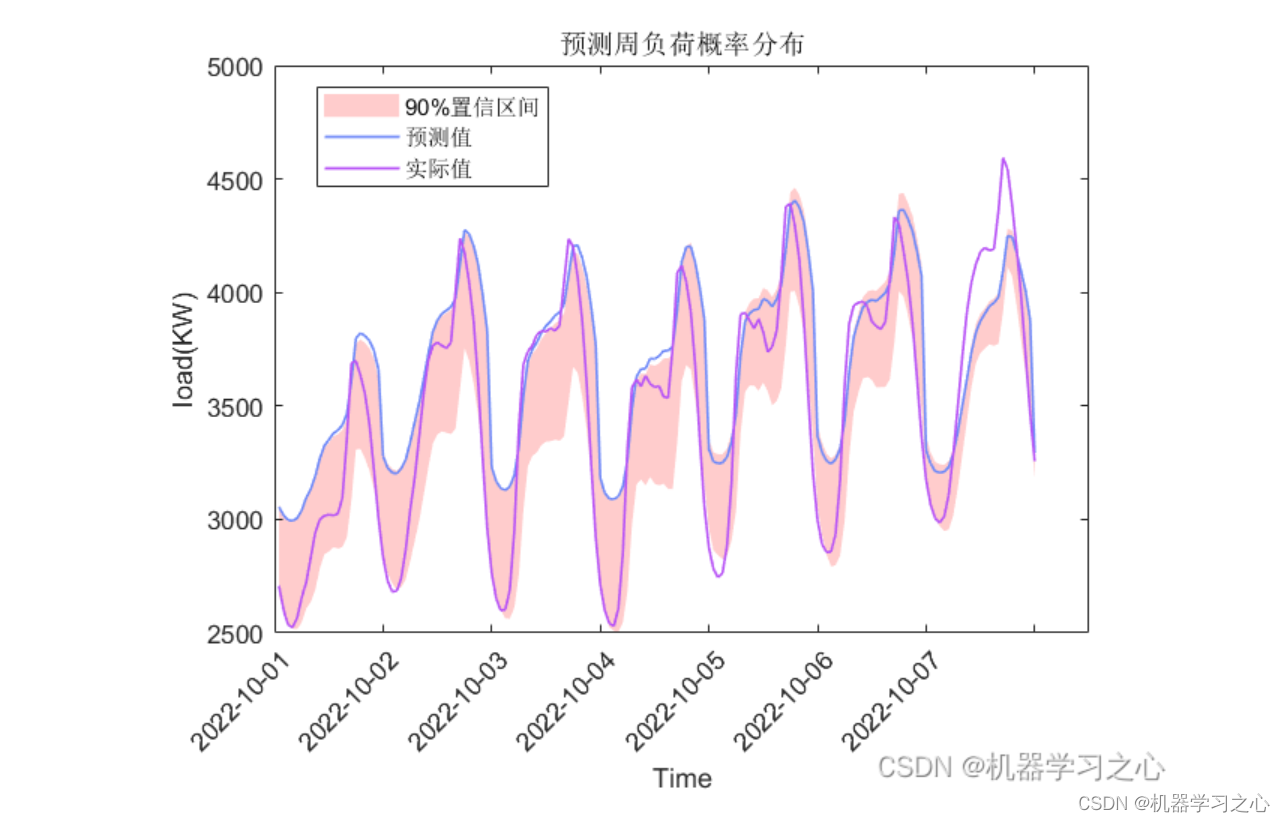
基本介绍

MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测

QRBiLSTM是一种双向长短期记忆(QR-LSTM)神经网络的变体，用于分位数回归时间序列区间预测。该模型可以预测时间序列的不同分位数的值，并且可以提供置信区间和风险评估等信息。
QR-LSTM是一种基于LSTM模型的分位数回归方法，可以通过学习分位数回归损失函数来预测不同分位数的值。而QRBiLSTM则是在QR-LSTM的基础上加入了双向传输的结构，可以捕捉更多的时间序列信息。

模型描述

QRBiLSTM模型的输入包括历史时间序列数据和外部变量，输出为时间序列的分位数值和置信区间。通常情况下，可以使用训练数据来拟合模型参数，并使用测试数据来评估模型的预测性能。在评估模型性能时，可以使用常见的指标如均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）等。
总之，QRBiLSTM是一种非常有用的时间序列预测模型，可以应用于许多领域，如金融、股票、气象学等，可以提供更全面的时间序列预测信息，有助于提高决策的准确性。

• 下面给出QRBiLSTM模型的具体公式，其中$\text{X}$表示输入序列，$\text{Y}$表示输出序列，$\text{H}$表示隐藏状态，$\text{C}$表示记忆状态，$f_{\theta }$表示神经网络模型，$q$表示分位数：

• 正向传播：

$${\text{H}}_t^f,{\text{C}}_t^f=LST{M}_{\theta }({\text{X}}_t,{\text{H}}_{t-1}^f,{\text{C}}_{t-1}^f)$$

$${\text{H}}_t^b,{\text{C}}_t^b=LST{M}_{\theta }({\text{X}}_t,{\text{H}}_{t+1}^b,{\text{C}}_{t+1}^b)$$

$${\hat{Y}}_t^q=f_{\theta }([{\text{H}}_t^f,{\text{H}}_t^b])$$

$${\widehat{ϵ}}_t^q=Y_t^q-{\hat{Y}}_t^q$$

σ ^ t q = median { ∣ ϵ ^ t − τ q ∣ : τ ≤ lag } ⋅ c α ( lag , n ) \hat{\sigma}^{q}_{t} = \text{median}\{|\hat{\epsilon}^{q}_{t-\tau}|:\tau \leq \text{lag}\} \cdot c_{\alpha}(\text{lag},n) σ^tq​=median{∣ϵ^t−τq​∣:τ≤lag}⋅cα​(lag,n)

• 其中，${\text{H}}_t^f$和${\text{C}}_t^f$分别表示正向传播的隐藏状态和记忆状态；${\text{H}}_t^b$和${\text{C}}_t^b$分别表示反向传播的隐藏状态和记忆状态；${\hat{Y}}_t^q$表示时间$t$处分位数为$q$的预测值；$f_{\theta }$表示神经网络模型；${\widehat{ϵ}}_t^q$表示时间$t$处分位数为$q$的预测误差；${\hat{\sigma }}_t^q$表示时间$t$处分位数为$q$的预测误差的置信区间，其中$c_{\alpha }(\text{lag},n)$表示置信系数。

• QRBiLSTM模型的训练目标是最小化分位数损失函数：

$${\text{Loss}}_{\theta }=\sum _{t=1}^T\sum _{q\in Q}{\rho }_q(|{ϵ}_t^q|)-\frac{1}{|Q|}\sum _{q\in Q}\text{log}({\hat{\sigma }}_t^q)$$

• 其中，${\rho }_q(x)$表示分位数损失函数：

$${\rho }_q(x)=\{\begin{array}{ll}qx& x\ge 0\\ (q-1)x& x<0\end{array}$$

• QRBiLSTM模型的预测目标是预测分位数值和置信区间，即${\hat{Y}}_t^q$和${\hat{\sigma }}_t^q$。

程序设计

• 基础版完整程序和数据获取方式，订阅《LSTM长短期记忆神经网络》(数据订阅后私信我获取):MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测
• 进阶版完整程序和数据获取方式：私信博主。

% 构建模型
numFeatures = size(XTrain,1); % 输入特征数
numHiddenUnits = 200; % 隐藏单元数
numQuantiles = 1; % 分位数数目
layers = [ ...
    sequenceInputLayer(numFeatures)
    bilstmLayer(numHiddenUnits,'OutputMode','last')
    dropoutLayer(0.2)
    fullyConnectedLayer(numQuantiles)
    regressionLayer];
options = trainingOptions('adam', ...
    'MaxEpochs',50, ...
    'MiniBatchSize',64, ...
    'GradientThreshold',1, ...
    'Shuffle','every-epoch', ...
    'Verbose',false);
net = trainNetwork(XTrain,YTrain,layers,options); % 训练模型

% 测试模型
YPred = predict(net,XTest); % 预测输出
quantiles = [0.1,0.5,0.9]; % 分位数
for i = 1:length(quantiles)
    q = quantiles(i);
    epsilon = YTest - YPred(:,i); % 预测误差
    lag = 10; % 滞后期数
    sigma = median(abs(epsilon(max(1,end-lag+1):end))) * 1.483; % 置信区间
    lb = YPred(:,i) - sigma * norminv(1-q/2,0,1); % 置信区间下限
    ub = YPred(:,i) + sigma * norminv(1-q/2,0,1); % 置信区间上限
    disp(['Quantile:',num2str(q),' MAE:',num2str(mean(abs(epsilon))),' Width:',num2str(mean(ub-lb))]);
end

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340