【数据结构】Treap树堆

news2024/12/28 20:36:28

Treap树堆

Treap是一种平衡化二叉搜索树，在键值key满足二叉搜索树的前提下，增加了priority是满足堆序的条件。可以证明，如果priority的随机的，那么Treap的期望深度是 $O (l o g N)$ ，也就是说大部分操作可以在 $O (l o g N)$ 的时间内完成。

基本数据定义

Treap就是Tree+heap，首先有二叉搜索树（BST）的数据，treapCnt记录当前的节点总数，节点和键值的映射key，每个节点的左右儿子childs，以及一个键可能存在多个副本，用cnt记录副本数，size记录子树大小，用于查找第k大元素。堆相关的数据：每个节点的优先级priority，这个优先级在创建节点时随机生成，保证了Treap的深度不会太大。

int root, treapCnt, key[maxNode], priority[maxNode];
int childs[maxNode][2], cnt[maxNode], size[maxNode];

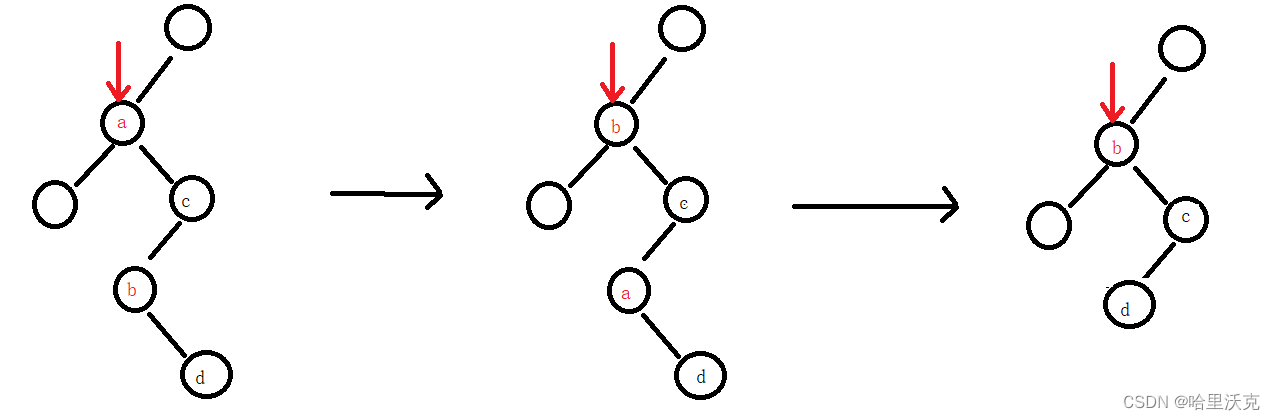
旋转操作

Treap的核心操作，通过旋转维护Treap堆的性质（父亲节点的键值大于它所有的儿子节点的）同时不会破坏BST的性质（父亲节点的键值大于左儿子的，大于右儿子的）。

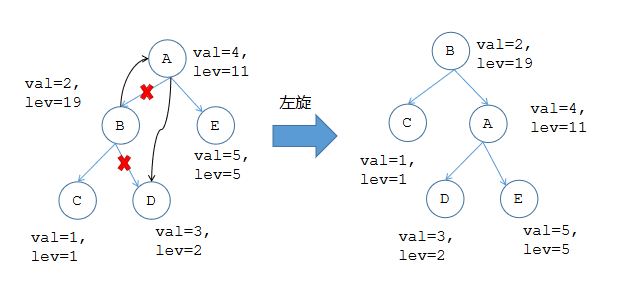
在这里插入图片描述

void rotate(int &x, int t) {
    // t=0/1对应左/右旋操作
    int y = childs[x][t];
    childs[x][t] = childs[y][1 - t];
    childs[y][1 - t] = x;
    // 旋转只会改变自己以及旋转上来的儿子节点
    update(x);
    update(y);
    x = y;
}

插入操作

插入操作在BST的插入基础上实现，插入节点递归返回的过程中，需要通过旋转“修复“堆的性质。

void _insert(int &x, int k) {
    if (x) {
        if (key[x] == k) {
            cnt[x]++;
        }   // 若节点已经存在，则副本数++
        else {
            int t = (key[x] < k);   // 根据BST性质进行插入
            _insert(childs[x][t], k);
            // 完成插入之后，通过旋转保持堆的性质
            if (priority[childs[x][t]] < priority[x]) {
                rotate(x, t);
            }
        }
    }
    else {  // 创建新节点
        x = treapCnt++;
        key[x] = k;
        cnt[x] = 1;
        priority[x] = rand();   // 随机优先级
        childs[x][0] = childs[x][1] = 0;
    }
    update(x);
}

删除操作

同样在BST删除操作的基础上，找到该目标节点之后，不可以直接删除之，需要将优先级更高的儿子节点旋转上来，作为新的父节点，其实可以理解为将待删除节点旋转至叶子节点再进行删除。
有一点要注意，删除一个节点之后，其编号将不再使用，下一个新创建节点的编号为treapCnt，因此在设置数组空间时，也就是确定maxNode时需要考虑极端情况，所有操作均为插入操作。

void _erase(int &x, int k) {
    if (key[x] == k) {
        if (cnt[x] > 1) {
            cnt[x]--;
        }   // 若节点不只1个副本，则副本数--
        else {
            if (childs[x][0] == 0 && childs[x][1] == 0) {
                x = 0;
                return;
            }   // 若没有儿子节点直接删除并返回
            // 否则需要将儿子旋转上来，再递归地进行删除
            int t = (priority[childs[x][0]] > priority[childs[x][1]]);
            rotate(x, t);
            _erase(x, k);
        }
    }
    else {  // 根据BST性质查找目标值
        _erase(childs[x][key[x] < k], k);
    }
    update(x);
}

luogu P3369

查询数x的排名，求数x的前驱/后驱，这3个操作根据BST的性质操作即可。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const int maxNode = 1e6 + 5;
struct Treap {
    int root, treapCnt, key[maxNode], priority[maxNode];
    int childs[maxNode][2], cnt[maxNode], size[maxNode];
    // treapCnt：树堆当前节点总数
    // 节点的基本属性：key：键值，priority：随机得到的优先级
    // childs:[i][0]代表左儿子，[i][1]代表右儿子
    // size: 维护子树大小，用于查询排名
    // cnt：每个节点包含的副本数
    Treap() {
        root = 0;
        treapCnt = 1;
        priority[0] = INT_MAX;
        size[0] = 0;
    }

    void update(int x) {
        size[x] = size[childs[x][0]] + cnt[x] + size[childs[x][1]];
    }

    void rotate(int &x, int t) {
        // t=0/1对应左/右旋操作
        int y = childs[x][t];
        childs[x][t] = childs[y][1 - t];
        childs[y][1 - t] = x;
        // 旋转只会改变自己以及旋转上来的儿子节点
        update(x);
        update(y);
        x = y;
    }

    void _insert(int &x, int k) {
        if (x) {
            if (key[x] == k) {
                cnt[x]++;
            }   // 若节点已经存在，则副本数++
            else {
                int t = (key[x] < k);   // 根据BST性质进行插入
                _insert(childs[x][t], k);
                // 完成插入之后，通过旋转保持堆的性质
                if (priority[childs[x][t]] < priority[x]) {
                    rotate(x, t);
                }
            }
        }
        else {  // 创建新节点
            x = treapCnt++;
            key[x] = k;
            cnt[x] = 1;
            priority[x] = rand();   // 随机优先级
            childs[x][0] = childs[x][1] = 0;
        }
        update(x);
    }

    void _erase(int &x, int k) {
        if (key[x] == k) {
            if (cnt[x] > 1) {
                cnt[x]--;
            }   // 若节点不只1个副本，则副本数--
            else {
                if (childs[x][0] == 0 && childs[x][1] == 0) {
                    x = 0;
                    return;
                }   // 若没有儿子节点直接删除并返回
                // 否则需要将儿子旋转上来，再递归地进行删除
                int t = (priority[childs[x][0]] > priority[childs[x][1]]);
                rotate(x, t);
                _erase(x, k);
            }
        }
        else {  // 根据BST性质查找目标值
            _erase(childs[x][key[x] < k], k);
        }
        update(x);
    }

    int _getKth(int &x, int k) {
        // 利用子树大小信息查找第k大值
        if (k <= size[childs[x][0]]) {
            return _getKth(childs[x][0], k);
        }
        k -= size[childs[x][0]] + cnt[x];
        if (k <= 0) {
            return key[x];
        }
        return _getKth(childs[x][1], k);
    }

    int _getRank(int x, int k) {
        if (!x) return 0;
        if (k == key[x]) return size[childs[x][0]] + 1;
        else if (k < key[x]) return _getRank(childs[x][0], k);
        else return size[childs[x][0]] + cnt[x] + _getRank(childs[x][1], k);
    }

    int getPre(int k) {
        int x = root, pre;
        while (x)
        {
           if (key[x] < k) { pre = key[x], x = childs[x][1]; }
            else x = childs[x][0];
        }
        return pre;
    }
    int getNxt(int k) {
        int x = root, nxt;
        while (x)
        {
           if (key[x] > k) { nxt = key[x], x = childs[x][0]; }
            else x = childs[x][1];
        }
        return nxt;
    }

    void insert(int k) {
        _insert(root, k);
    }
    void erase(int k) {
        _erase(root, k);
    }
    int getKth(int k) {
        return _getKth(root, k);
    }
    int getRank(int k) {
        return _getRank(root, k);
    }
} mTreap;

// luogu P3369
void solve() {
    int n; cin >> n;
    int op, x;
    while (cin >> op >> x) {
        switch (op)
        {
        case 1:
            mTreap.insert(x);
            break;
        case 2:
            mTreap.erase(x);
            break;
        case 3:
            cout << mTreap.getRank(x) << '\n';
            break;
        case 4:
            cout << mTreap.getKth(x) << '\n';
            break;
        case 5:
            cout << mTreap.getPre(x) << '\n';
            break;
        case 6:
            cout << mTreap.getNxt(x) << '\n';
            break;
        }
    }
}

双端队列

这个问题我在数据结构与算法课上想过，并且在知乎上还提问了233。后来在校赛上遇到了同样的问题！当时手上一本上交的《ACM国际大学生程序设计竞赛算法与实现》，看到了Treap可以查询第k大数的操作，当时灵机一动似乎可以搞，在赛场上解决了这个脑海里悬而未决的问题。实际上，所有平衡树通过维护子树大小，都可以实现查询第k大数的操作。不过，个人感觉Treap仅仅在BST的基础上增加priority一个随机属性并辅以旋转操作维护堆的性质，实在妙哉！

问题描述：维护一个双端队列，支持两个操作，1 x输出第x个元素，并将其移至队尾，2 x输出第x个元素，并将其移至队首。队内初始有n个元素，共有m次操作，n,m均是5e5的数量级。

我的做法：通过一个哈希表维护<key, element>，操作1通过getKth操作获取到该元素并输出，可以通过设置key为当前最小的key减1再将其插入Treap中，那么它将是Treap中最小的元素，也就是队首元素。操作2同理。

代码如下，Treap类省略。

unordered_map<int, int> mp;

void solve() {
    int n, m;
    cin >> n >> m;
    int a;
    for (int i = 1; i <= n; i++) {
        cin >> a;
        mp[i] = a;
        mTreap.insert(i);
    }
    int k, x;
    int l = 1, r = n;
    for (int i = 1; i <= m; i++) {
        cin >> k >> x;
        if (k == 1) {
            int ret = mTreap.getKth(x);
            cout << mp[ret] << '\n';
            mTreap.erase(ret);
            r++;
            int tmp = mp[ret];
            mp.erase(ret);
            mp[r] = tmp;
            mTreap.insert(r);
        }
        else {
            int ret = mTreap.getKth(x);
            cout << mp[ret] << '\n';
            mTreap.erase(ret);
            l--;
            int tmp = mp[ret];
            mp.erase(ret);
            mp[l] = tmp;
            mTreap.insert(l);
        }
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/508386.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！