1.二叉搜索树的公共祖先

235. 二叉搜索树的最近公共祖先

不同于普通二叉树，二叉搜索树得益于其顺序结构，其公共祖先的查找也有迹可循。自顶向下递归遍历，只要一个节点的val夹在p和q之间，那么该节点就是最近公共祖先。

1.首先公共祖先是必然的，因为val夹在q和p之间；

2.”最近“ 这个结论如何得到，我们假设它(cur1)不是最近的公共祖先，那么一定有另一个公共祖先(cur2)，但是此时是冲突的，因为cur1不等于cur2，但是cur1在q和p之间，cur2也在p和q之间，cur1的子节点是cur2，cur1的左右某一分支一定包括了q和p，而不会在两边，所以矛盾

3.如果cur递归到空，返回空

4.那么如果递归下去，cur的值大于p和q的，那么我们要遍历cur左边，如果左边递归接住了节点，那么我们返回左边接住的节点

5.cur的值小于p和q的，那么我们要遍历cur右边，如果右边递归接住了节点，那么我们返回右边接住的节点

6.如果不是左右递归，说明此时q和p的父节点就是公共祖先，我们直接返回cur即可

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr)
            return nullptr;
        if(root->val>p->val&&root->val>q->val)
        {
            TreeNode* left = lowestCommonAncestor(root->left,p,q);
            if(left!=nullptr)
                return left;
        }
        else if(root->val<p->val&&root->val<q->val)
        {
            TreeNode* right = lowestCommonAncestor(root->right,p,q);
            if(right!=nullptr)
                return right;
        }
        return root;
    }
};

2.二叉搜索树的节点插入

701. 二叉搜索树中的插入操作

非递归写法

1.如果root本身是空，root更新即可

2.此外，无非就是根据大小走左右，直到cur为空，不过在遍历时也要有prev前驱节点，保证最后cur到空，prev能与新节点连接

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        if(root==nullptr)
        {
            root=new TreeNode(val);
            return root;
        }  
        while(cur)
        {
            if(cur->val>val)
            {
                prev=cur;
                cur=cur->left;
            }
            else
            {
                prev=cur;
                cur=cur->right;
            }
        }
        cur=new TreeNode(val);
        if(prev->val>cur->val)
            prev->left=cur;
        else
            prev->right=cur;
        return root;
    }
};

递归法

1.如果走到nullptr，说明此时需要建立节点

2.如果根节点的数值大，走左边，此时需要root->left接住最后也要构造的节点

3.如果根节点的数值小，走右边，也要root->right接住

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root==nullptr)
            return new TreeNode(val);
        if(root->val>val)
            root->left=insertIntoBST(root->left,val);
        else if(root->val<val)
            root->right=insertIntoBST(root->right,val);
        return root;
    }
};

3.二叉搜索树的节点删除

450. 删除二叉搜索树中的节点

首先删除工作一定涉及到前驱节点，所以我们找节点还得顺便将其前驱节点找到。

那在我看来其实就三种情况的删除工作：cur为删除节点，prev为前驱节点

情况一：右节点为空

 有两中大情况：

root是删除的节点，那么我们更新root为cur的left；

root不是删除的节点：此时我们需要更新prev，注意prev的左节点还是右节点是cur，再连接：如果prev的left是cur，那么是prev的left与cur的right连接；如果prev的right是cur，那么是prev的right与cur的right连接

情况二：左节点为空

与上面的情况基本一致：

root是删除的节点，那么我们更新root为cur的right；

root不是删除的节点：此时我们需要更新prev，注意prev的左节点还是右节点是cur，再连接：如果prev的left是cur，那么是prev的left与cur的left连接；如果prev的right是cur，那么是prev的right与cur的left连接

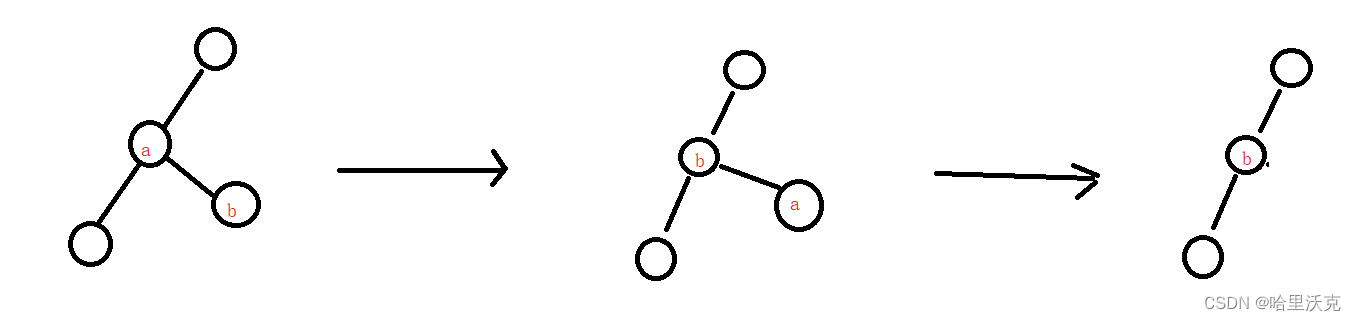
情况三：左右都有

此时cur要么找左节点的最大值，要么找右节点的最小值交换，再删除cur值

左节点的最大值：左边树的最右节点

右节点的最小值：右边树的最左节点

那我这里写的是和右节点的最小值交换

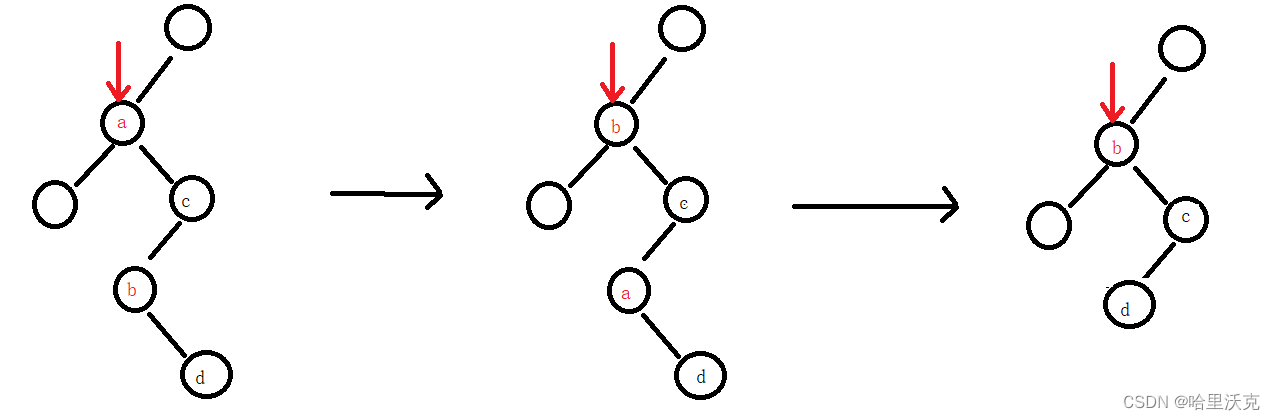
这两个的操作基本一致：

1.我们先找到最左节点tmp，当然还需要这个的前驱ptmp

2.随后交换 cur和tmp的值

3.ptmp和tmp的位置判断，将ptmp和tmp的后续连接起来

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur)
        {
            if(cur->val>key)
            {
                prev=cur;
                cur=cur->left;
            }
            else if(cur->val<key)
            {
                prev=cur;
                cur=cur->right;
            }
            else
            {
                if(cur->right==nullptr)
                {
                    if(cur==root)
                        root=cur->left;
                    else
                        if(prev->left==cur)
                            prev->left=cur->left;
                        else
                            prev->right=cur->left;
                    delete cur;
                }
                else if(cur->left==nullptr)
                {
                    if(cur==root)
                        root=cur->right;
                    else
                        if(prev->left==cur)
                            prev->left=cur->right;
                        else
                            prev->right=cur->right;
                    delete cur;
                }
                else
                {
                    TreeNode* ptmp = cur;
                    TreeNode* tmp = cur->right;
                    while(tmp->left)
                    {
                        ptmp=tmp;
                        tmp=tmp->left;
                    }
                    cur->val=tmp->val;
                    if(ptmp->right==tmp){
                        ptmp->right=tmp->right;
                    }
                    else
                        ptmp->left=tmp->right;
                    delete tmp;
                }
                break;
            }
        }
        return root;
    }
};