💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:

本文提出了一种新的混合算法GA-RRHC,该算法基于遗传算法(GA)和随机重启爬山(RRHC)算法,用于优化具有高度灵活性的柔性作业车间调度问题(FJSSP)(其中每个操作都可以由大量机器完成)。特别是,不同的GA交叉和简单变异算子与细胞自动机(CA)启发的邻域一起使用,以执行全局搜索。该方法通过基于RRHC的局部搜索进行改进,使计算实现变得简单。通过在GA-RRHC中应用CA型邻域并混合上述两种技术,获得了新的点,这易于理解和实现。GA-RRHC通过文献中广泛使用的四组实验进行测试,并使用相对百分比偏差(RPD)和弗里德曼测试将其结果与最近的六种算法进行比较。实验表明,对于FJSSP实例,GA-RRHC与其他最近的算法相比是一种具有竞争力的方法,具有很高的灵活性。
本文提出了一种新的混合技术,称为GA-RRHC,它结合了两种元启发式技术:第一种是使用遗传算法(GA)算子进行全局搜索,另一种是基于细胞自动机(CA)概念的邻域,主要用于操作顺序的编程。作为第二步,每个解决方案都通过应用随机重新启动爬坡(RRHC)的局部搜索来细化,特别是为了对关键操作的机器进行最佳选择,这对于具有高度灵活性的问题更为方便。重启被用作一种简单的策略,以避免解决方案过早收敛,这项研究的贡献在于最初使用了两种易于实现的运算符来定义一种稳健的混合技术,该技术可以为FJSSP的实例找到满意的解决方案,以最小化所有作业的处理时间(或制造时间)。
本文的结构如下:第2节提供了FJJSP的正式表示。第3节提出了新的GA-RRHC方法,解释了所使用的遗传算子、解决方案种群进化的CA启发邻域以及RRHC的操作,以细化每个解决方案。第4节讨论了GA-RRHC的参数调整,与文献中常用的四个FJSSP数据集中的其他六个最近发表的算法进行了比较,并根据非参数Friedman检验和相对百分比偏差(RPD)进行了统计分析。第5节给出了本文的结论。
📚2 运行结果
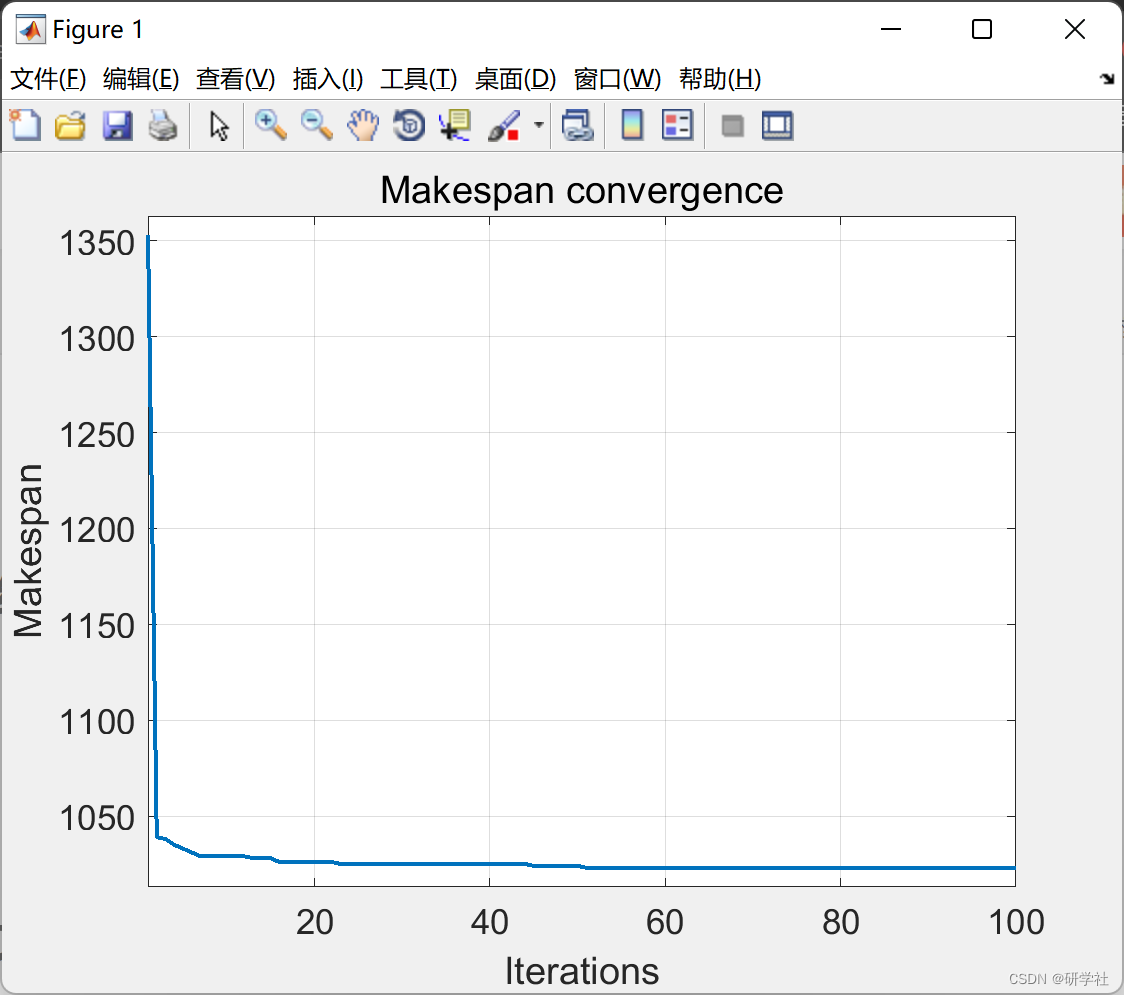
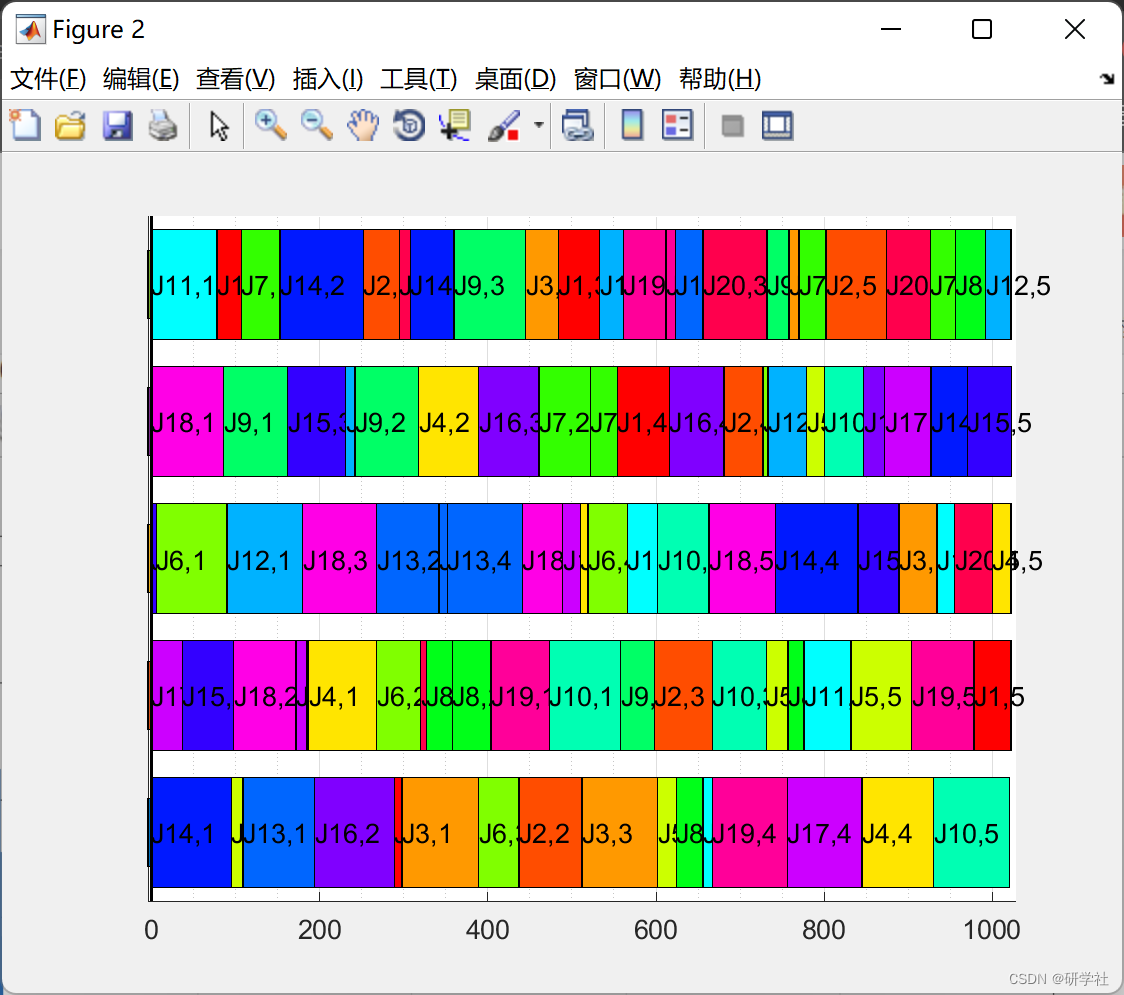
 部分代码:
部分代码:
archivo=fopen(nombreArchivo,'r');
datos=fscanf(archivo,'%f');
numeroTrabajos=datos(1);
numeroMaquinas=datos(2);
vectorOperaciones=[];
%Indices to take jobs, operations and positions
indice=4;
nt=1;
%Loop for jobs
while(nt<=numeroTrabajos)
vectorNumOperaciones(nt)=datos(indice);
vectorInicioOperaciones(nt)=sum(vectorNumOperaciones(1:nt-1));
operacionesTrabajo=ones(1,vectorNumOperaciones(nt))*nt;
vectorOperaciones=[vectorOperaciones operacionesTrabajo];
%Loop for operations
for numOper=1:vectorNumOperaciones(nt)
indice=indice+1;
numMaq=datos(indice);
%Loop for machines
for i=1:numMaq
indice=indice+1;
maquina=datos(indice);
indice=indice+1;
tiempo=datos(indice);
tablaTiempos(vectorInicioOperaciones(nt)+numOper,maquina)=tiempo;
end
end
%Next job
indice=indice+1;
nt=nt+1;
end
%Operation number
numeroOperaciones=length(vectorOperaciones);
%Available machines per operation
tablaMaquinasFactibles=[];
for oper=1:length(tablaTiempos)
indices_factibles = tablaTiempos(oper,:) ~= 0;
tablaMaquinasFactibles=[tablaMaquinasFactibles; indices_factibles];
end
end
%Algorithm GA_RRHC
function [mejorSO, mejorSM, mejorMakespan, PoblacionSO, PoblacionSM, PoblacionMakespan, convergencia, contIt] = GA_RRHC(numIndividuos, numGeneraciones, numEstancamiento, probElitista, numeroTrabajos, numeroMaquinas, numOperaciones, vectorNumOperaciones, vectorInicioOperaciones, vectorOperaciones, tablaTiempos, tablaMaquinasFactibles,numVecinos,probMutacion,iteracionesTotalesEscalada,iteracionesReinicioEscalada,probOperCrit,bandImp)
%Initialize values
mejorSO = [];
mejorSM = [];
mejorMakespan = inf;
convergencia = [];
%Population vectors
PoblacionSO=zeros(numIndividuos,numOperaciones);
PoblacionSM=zeros(numIndividuos,numOperaciones);
PoblacionMakespan=zeros(numIndividuos,1);
%Table with the characteristics of each solution concerning the jobs,
%It is sorted by jobs and the order of their operations (J_11, J_12, ... Jnm-1, Jnm)
%Rows keep in this order the information:
%Machine assigned
%Processing position on the assigned machine
%End of operation time
%Operation duration
%Tail time
%Operation position in SO
%Operation position in SM
PoblacionTablaTrabajos=zeros(6,numOperaciones,numIndividuos);
%Table with the characteristics of each solution concerning the machines,
%It is sorted by machines and the order of their operations (M_11, M_12, ... Mmo-1, Jmo)
%Rows keep in this order the information:
%Scheduled work
%Operation of scheduled work
%Final operation time
%Operation duration
%Tail time
%Operation position in SO
%Operation position in SM
PoblacionTablaMaquinas=zeros(6,numOperaciones,numIndividuos);
🎉3 参考文献
部分理论来源于文献,如有侵权请;联系删除。