前言
在上期,使用一个简单的一维应用实例来加深了卡尔曼滤波的印象后,使用一个二维的例子来看一下卡尔曼的效果。使用一个自由落体的例子来说明,假设一个物体在重力作用下,速度由0开始做自由落体运动,有观测装置对该物体的位移进行观测,每 1 秒测量一次数据,规定向下为正,也就是说,加速度 a = g,状态方程的原始模型还是如下的形式:
X(k) = A*X(k-1) + B*u(k-1) + w(k-1)
Z(k) = H*X(k) + v(k)
其中 w 为过程噪声,方差为Q, v 为测量噪声,方差为R
状态方程的建立
根据自由落体的公式,可以建立如下的方程:
速度 v = a*t
位移 s = a*t*t / 2
写成离散的形式为:
速度 v(k) = v(k-1) + a * dt
位移 s(k) = s(k-1) + [v(k-1) + v(k)] * dt / 2
由于 v(k) = v(k-1) + a * dt,因此 s(k) = s(k-1) + v(k-1) * dt + a*dt/2
为了方便计算,我们将 dt 设置为1,也就是 1 秒作为时间间隔进行观测与估算,同时,a = g,那么上式就会简化为:
v(k) = v(k-1) + g
s(k) = s(k-1) + v(k-1) + 0.5 * g
将上式写作状态方程的形式,定义 x1 代表位移,x2 代表速度,x1_dot = x2 (x1的微分就是x2),将x1,x2合并为一个二维的状态矩阵 x
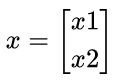
则离散形式的状态方程为:

测量方程为:
z(k) = [1 0]x(k) + r(k)
其中,r 为测量噪声,传感器只能观测位移,不能观测速度
matlab程序编写
同上篇文章的一维应用一样,对系统各个参数先进行赋值,按照上面建模的模型数据进行赋值即可,需要注意的是 Q 矩阵,赋值为 x1 的方差与 x2 的方差:
N = 10; %采样个数 每1s采样一次,采样100s
temp_real = 0; %实际距离
%系统状态方程为:
% X(k) = A*X(k-1) + B*u(k-1) + w(k-1)
% Z(k) = H*X(k) + v(k)
% 其中 w 为过程噪声,方差为Q, v 为测量噪声,方差为R
% u输入为重力加速度 g
A = [1 1; 0 1]; %
B = [0.5;1];
u = 9.8; %输入为重力加速度
H = [1 0]; %由于是一维系统,因此H矩阵为1
Q = [1^2 0; 0 1^2]; %假定过程噪声的方差为1*1 即加入空气阻力等因素的影响造成的系统建模误差
R = 10.0^2; %假定测量噪声的方差为1.0*1.0
x_real = temp_real*ones(2,N); %将实际值赋值二维容器中
x_hat = zeros(2,N); %先验估计值 二维
xhat = zeros(2,N); %估计值
z = zeros(1,N); %位移传感器测量值
P = Q; %协方差矩阵 初始为Q
P_ = P; %先验协方差矩阵
z(1) = 0; %初始位移
x_hat(1) = z(1); %初始估计值
w = sqrt(Q)*randn(2,N); %过程噪声 方差的开方就是噪声的大小
v = sqrt(R)*randn(1,N); %测量噪声 方差的开方就是噪声的大小之后,按照卡尔曼滤波的五大公式,进行数据更新:

在编程时,需要注意一点,在计算卡尔曼增益时,上篇的一维系统,由于矩阵都是一维,因此是可以直接使用 '/' 除号的,但矩阵非一维后,需要使用 inv 来求矩阵的逆来代替除号。
除此之外,在更新实际值时,让真实位移再增加一个在方差范围内的误差,模拟空气阻力等因素的影响:
for k = 2:N
%修改实际值,让真实温度每次递增 但增量需要在方差以内
x_real(:,k) = A*x_real(:,k-1) + B * u + w(:,k);
%获取测量值
z(k) = H * x_real(:,k) + v(k); %加入测量噪声
%计算先验估计值
x_hat(:,k) = A * xhat(:,k-1);
%计算先验协方差
P_ = A * P * A' + Q;
%计算卡尔曼增益 由于是二维矩阵,因此不能直接使用/除号,需要使用inv来求逆
K = (P_ * H') * inv(H * P_ * H' + R);
%计算后验估计值
xhat(:,k) = x_hat(:,k) + K * (z(k) - H * x_hat(:,k));
%更新估计误差协方差
P = (1 - K * H) * P_;
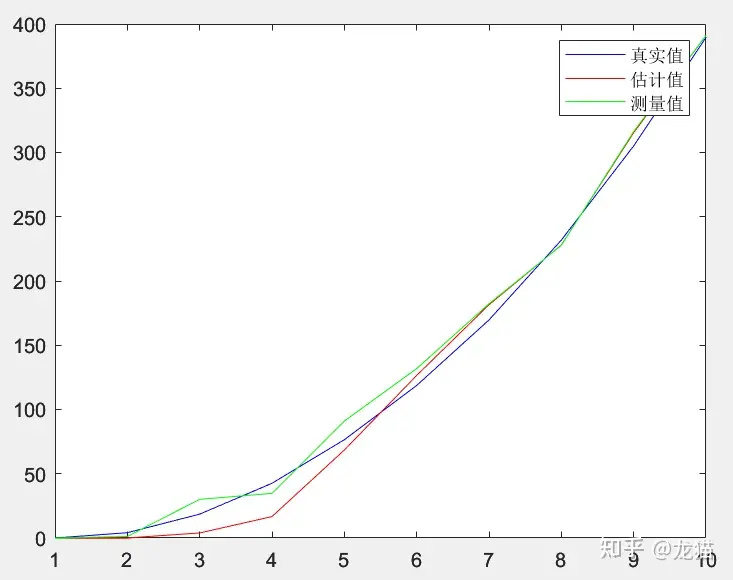
end画出数据的对比图: