---

一、位运算的知识点

位运算两个性质：

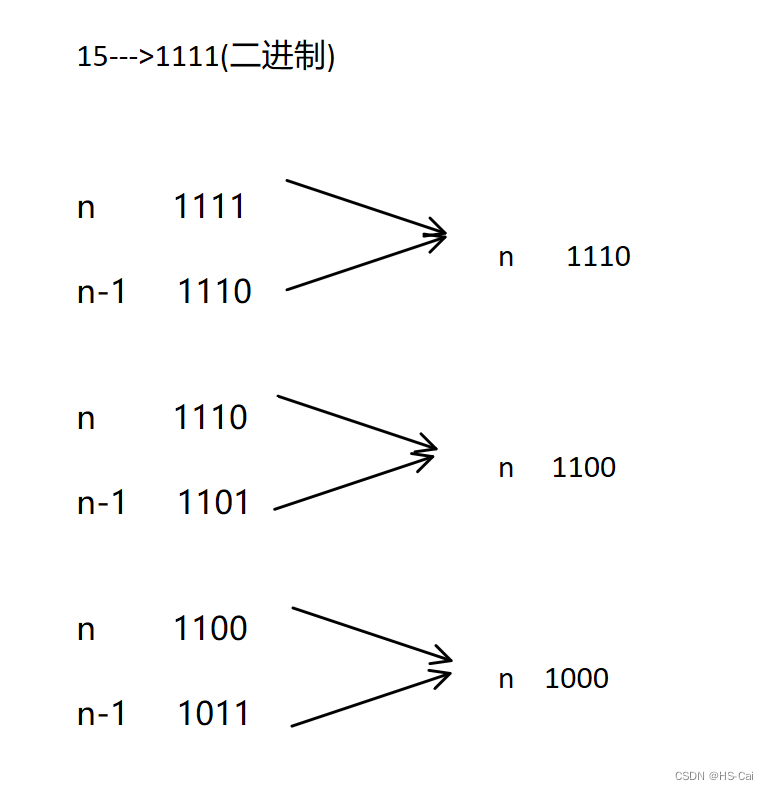
• x & (−x)：保留二进制下最后出现1的位置，其余位置为0。（-x 等同于 ~x + 1）
• x & (x − 1)：消除二进制下最后出现1的位置，其余保持不变。

x & (x - 1)的原理图：

二、位运算的应用

1. x & 1

一个数补码表示中的第k位数字

int func(int n, int k)
{
	return ((n >> k) & 1);
}

求补码中含有1的个数

int func(int n)
{
	int countn = 0;
	while (n)
	{
		if (n & 1) countn++;
		n = n >> 1;
	}
	return countn;
}

偶数位与奇数位分开输出

void func(int n)
{
	std::cout << "奇数位输出:>";
	for (int i = 31; i >= 1; i -= 2)
	{
		std::cout << ((n >> i) & 1) << ' ';
	}
	std::cout << std::endl << "偶数位输出:>";
	for (int i = 30; i >= 0; i -= 2)
	{
		std::cout << ((n >> i) & 1) << ' ';
	}
}

2. x & (-x)

返回x的最后一位1及之后的数字

lowbit(x)：返回x的最后一位1及之后的数字

x=101000 lowbit(x)=1000
x=1010 lowbit(x)=10

判断一个数是否是2的n次方

bool func(int n)
{
	return (n == (n & (-n)));
}

求补码中含有1的个数

int func(int n)
{
	int countn = 0;
	while (n)
	{
		countn++;
		n -= (n & (-n));
	}
	return countn;
}

3. x & (x - 1)

求补码中含有1的个数（微软）

int func(int x)
{
	int countx = 0;
	while (x)
	{
		countx++;
		x = x & (x - 1);
	}
	return x;
}

判断一个数是否是2的n次方

bool func(int x)
{
	x = x & (x - 1);
	return x ? false : true;
}

两个数补码位上不同数的数量

int func(int x, int y)
{
	int ret = x ^ y, count = 0;
	while (ret)
	{
		count++;
		ret = ret & (ret - 1);
	}
	return count;
}