1. 原理介绍

在目标检测，视频分类等大型计算机视觉应用中，受到计算机内存的限制，必须设置较小的样本数量，但是样本量小势必会导致批归一化的性能有所影响。

分组归一化（Group Normalization，GN）是针对批归一化算法对批次大小依赖性强这一弱点而提出的改进算法。因为 BN 层统计信息的计算与批次的大小有关，因此当批次变小时，很明显统计均值和方差的计算会越不准确和稳定，最终会有小批次高错误率的这一现象发生。

分组归一化 GN 介于层归一化 LN 和实例归一化 IN 之间，对于输入大小为 [N,C,H,W] 的图像，N 代表批次的大小，C 表示输入通道数，H,W 表示输入图片高度和宽度。

分组归一化首先将输入通道 C 分为 G 个小组，然后分别对每一小组做归一化操作，也就是先把输入的特征维度由 $[N,C,H,W]$ 变成 $[N,G,\frac{C}{G},H,W]$ ，归一化的维度为 $[\frac{C}{G},H,W]$ 。

事实上，当 G 等于 1 时，即所有的输入通道为 1 组时 GN 与 LN 的计算方式相同，而当 G 等于 C 时，1 个输入通道为 1 组时 GN 与 IN 的计算方式相同。

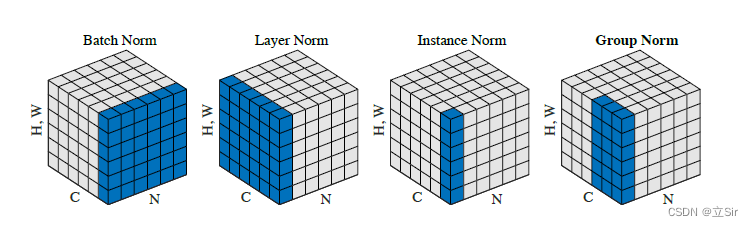
上图是批归一化算法 BN、层归一化算法 LN、实例归一化 IN 和分组归一化 GN 的简单图示。图中的立方体是三维，蓝色的方块是各个算法计算均值和方差的区域。

其中 C 代表通道数，N 是批量大小，H,W 是高度和宽度，第三个维度的大小是 H*W，这样输入就可以用三维图形来表示。从上图中可以看出只有 BN 的计算与批次大小 N 有关，LN、IN 和 GN 的计算都在单个样本上进行， LN、IN 和 GN 三者可相互转换。

通常来说，归一化的方式如下所示：

$\mu_i=\frac{1}{m}\sum_{k\in S_i}x_k$

$\sigma_i=\sqrt{\frac{1}{m}\sum_{k\in S_i}\left(x_k-\mu_i\right)^2+\epsilon}$

$S_i$ 是均值和方差的计算区域，在 BN 中有：

$S_i=\left\{k|k_C=i_C\right\}$

在 LN 中：

$S_i=\left\{k|k_N=i_N\right\}$

在 GN 中：

$S_i=\{k\mid k_N=i_N,floor(\frac{k_C}{C/G})=floor(\frac{i_C}{C/G})\}$

优点：不依赖批量大小。

缺点：当批量大小较大时，性能不如BN。

2. 代码展示

import torch 
from torch import nn

class GN(nn.Module):
    # 初始化
    def __init__(self, groups:int, channels:int, 
                 eps:float=1e-5, affine:bool=True):
        super(GN, self).__init__()
        # 通道数要整除组数
        assert channels % groups == 0, 'channels should be evenly divisible by groups'
        self.groups = groups  # 把通道分成多少组
        self.channels = channels  # 通道数
        self.eps = eps  # 防止分母为0
        self.affine = affine  # 是否使用可学习的线性变化参数
        if self.affine:
            self.scale = nn.Parameter(torch.ones(channels))  # 缩放因子
            self.shift = nn.Parameter(torch.zeros(channels))  # 偏置
    # 前向传播
    def forward(self, x: torch.Tensor):
        x_shape = x.shape  # 输入特征的维度 [b,c,w,h]
        batch_size = x_shape[0]  # 样本量
        assert self.channels == x.shape[1]  # 预设通道数和输入特征的通道数要保持一致
        # [b,c,w,h]-->[b,g,w*h*c/g]
        x = x.view(batch_size, self.groups, -1)
        # 在最后一个维度上做标准化
        mean = x.mean(dim=[-1], keepdim=True)  # [b,g,1]
        mean_x2 = (x**2).mean(dim=[-1], keepdim=True)  # [b,g,1]
        var = mean_x2 - mean**2
        x_norm = (x-mean) / torch.sqrt(var+self.eps)  # [b,g,w*h*c/g]
        # 线性变化
        if self.affine:
            x_norm = x_norm.view(batch_size, self.channels, -1)  # [b,c,w*h]
            x_norm = self.scale.view(1,-1,1)* x_norm + self.shift.view(1,-1,1)  # [1,c,1]*[b,c,w*h]+[1,c,1]
        # [b,c,w*h]-->[b,c,w,h]
        return x_norm.view(x_shape)

# ---------------------------------- #
# 验证
# ---------------------------------- #

if __name__ == '__main__':
    # 构造输入层
    x = torch.linspace(0, 47, 48, dtype=torch.float32)  # 构造输入层
    x = x.reshape([2,6,2,2])  # [b,c,w,h]
    # 实例化
    gn = GN(groups=3, channels=6)
    # 前向传播
    x = gn(x)
    print(x.shape)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/505912.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！