文章目录

思想&框架
- 1.组合/子集和排列问题
- 2.组合应用问题
组合/子集问题
- 1. lc77 组合
- 2. lc216 组合总和III
- 3. lc39 组合总和
- 4. lc40 组合总和II
- 5. lc78 子集
- 6. lc90 子集II
排列
- 1. 全排列I
- 2. 全排列II
组合问题的应用
- 1.lc17 电话号码的字母组合
- 2.lc131 分割回文串
- 3. lc19 复原IP地址
岛屿问题&棋盘问题

思想&框架

首先统一的框架是：

result = []
def dfs(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
       dfs(路径, 选择列表)
        撤销选择

其实就是把回溯问题看成一个多叉树，for循环去遍历树的宽度，dfs回溯去深度遍历

主要有这么几类问题：组合/子集和排列，岛屿问题，分割问题，棋盘问题

1.组合/子集和排列问题

第一个大类就是组合/子集和排列问题，围绕着元素重不重复，可不可以复选来
基本技巧就是：
组合/ 子集：startIndex
排列：used数组&排序

具体点的关键代码（来点投机取巧速记的）
组合/子集

元素不重复且不可重复选：dfs(n,k,i+1)
元素不重复且可重复选：dfs(n,k,i)
元素重复且不可重复选：排序 & nums[i]==nums[i-1]判断

排列

元素不重复：used数组，
元素重复：排序+nums[i]==nums[i-1]判断+used数组

2.组合应用问题

需要灵活运用，不单单是上面几种的变种，更多的是回溯思维的提升

组合/子集问题

子集和组合问题基本一致，唯一不同就是子集收集的是树的所有节点，而组合收集的是叶子节点。

1. lc77 组合

力扣链接

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合
输入：n = 4, k = 2
输出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4],]

Solution
（记住下面这个基本的板子！）

    // 两个全局变量（也可以放进递归的参数中）
    List<List<Integer>> list = new ArrayList<>(); // 存放结果集
    LinkedList<Integer> path = new LinkedList<>();  // 存放每次的结果
     
    public  List<List<Integer>> combine(int n, int k) {
        backTracking(n,k,1);
        return list;
    }

    public void  backTracking(int n,int k,int startIndex)
    {
        if(path.size()==k)
        {
            // 注意这里要新建ArrayList的path
            list.add(new ArrayList<>(path));
            return;
        }
        //for(int i=startIndex;i<=n;i++)，i<=n-(k-path.size())+1 是剪枝操作
        for(int i=startIndex;i<=n-(k-path.size())+1;i++)
        {
            path.add(i);
            backTracking(n,k,i+1);
            path.removeLast();
        }
    }

两个细节：
（1）一个是list.add(new ArrayList<>(path));，为什么不能直接add(path)？
因为变量 path 所指向的列表在深度优先遍历的过程中只有一份，深度优先遍历完成以后，回到了根结点，成为空列表。
在 Java 中，参数传递是值传递，对象类型变量在传参的过程中，复制的是变量的地址。这些地址被添加到 res 变量，但实际上指向的是同一块内存地址，因此我们会看到 66 个空的列表对象。解决的方法很简单，在 res.add(path); 这里做一次拷贝即可。
（链接：https://leetcode.cn/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/）

(2) 另一个就是剪枝，怎么判断剪枝条件？
可以这么想，i是有搜索上界的，i越大，剩下可选的数就越少，这样就不满足k的要求，也就没必要再搜索下去。
要组成大小为k的path，此时还需要k - path.size()个数，如果[i, n]这个区间内，(有n - i + 1个数)不足这么多，则肯定没有结果，直接剪枝。则 k-path.size()<n-i+1，所以i=n-(k-path.size())+1，也就是i的上界。

2. lc216 组合总和III

lc216 链接

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：只使用数字1到9,每个数字最多使用一次 .返回所有可能的有效组合的列表。该列表不能包含相同的组合两次
输入: k = 3, n = 9 输出: [ [1,2,6], [1,3,5], [2,3,4] ]

Solution:
与上题相似，多了一个对sum的判断。可以选择的数字是1-9

 List<List<Integer>> res= new ArrayList<>();
 LinkedList<Integer> path = new LinkedList<>();
 public List<List<Integer>> combinationSum3(int k, int n) {
     backTrack(k,n,1,0);
     return res;
 }

 void backTrack(int k,int n,int startIndex,int sum)
 {
     // 剪枝操作，如果sum已经大于n，直接返回
     if(sum>n)
         return;
     
     // 终止条件
     if(path.size()==k)
     {
         if(sum==n)
             res.add(new ArrayList<>(path));

         return;
     }
     // 当然，这里也可以模仿上面再剪枝，写成i<=9-(k-path.size())+1
     for(int i=startIndex;i<=9;i++)
     {
         path.add(i);
         sum += i;
         backTrack(k,n,i+1,sum);
         path.removeLast();
         sum -= i;
     }
 }

3. lc39 组合总和

lc39 链接

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。candidates 中的同一个数字可以无限制重复被选取。
输入: candidates = [2,3,5], target = 8 输出: [ [2,2,2,2],[2,3,3],[3,5] ]

Solution:
与前两题组合不同（特别是组合总和III），这里选取的数字的可以重复的，想一想前两题是怎么控制不重复选的，startIndex！每次dfs时都加一，这样就确定了遍历起点。所以，当可以重复时，就不用加一了！
（如果要问为什么还需要startIndex，因为这还是组合问题啊，也就是不能走回头路，比如[1,2,3]，目标和是4，你可以选[1,1,2]，如果没有startIndex，当你到2的时候，又会有[2,1,1]的可能！）

 List<List<Integer>> res = new ArrayList<>();
 LinkedList<Integer> path  =new LinkedList<>();
 public List<List<Integer>> combinationSum(int[] candidates, int target) {
     backTrack(candidates,target,0,0);
     return res;
    
 }
 void backTrack(int[] candidates,int target,int sum,int startIndex)
 {     
     if(sum>=target)
     {
         if(sum==target)
            res.add(new ArrayList<>(path));
         return ;
     }
     for(int i=startIndex;i<candidates.length;i++)
     {
         path.add(candidates[i]);
         sum+=candidates[i];
         // 注意这里，因为可以重复，所以不需要i+1了
         backTrack(candidates,target,sum,i);
         sum-=candidates[i];
         path.removeLast();
     }
 }

4. lc40 组合总和II

lc40链接

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次
输入: candidates = [2,5,2,1,2], target = 5,
输出: [ [1,2,2], [5] ]

Solution:
与上一题的区别在于如何去重，因为原始的候选集有重复元素，如果还是按照上面的思路的话，结果集肯定有重复的。解决方法是排序＋相邻相等判断！

  class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates); // 注意这里先排序
        dfs(candidates,target,0,0);
        return res;
    }
     public void dfs(int[] nums,int target,int sum,int startIndex)
    {
        if(sum>target) return;
        if(sum==target)
        {
            res.add(new LinkedList<>(path));
            return;
        }
        for(int i=startIndex;i<nums.length;i++)
        {
        // 注意这里的去重，当i不是startIndex时，要判断与前一个数字是否相同
            if(i>startIndex && nums[i]==nums[i-1])
               continue;
            path.add(nums[i]);
            sum+=nums[i];
            dfs(nums,target,sum,i+1);
            sum-=nums[i];
            path.removeLast();
        }
    }
}

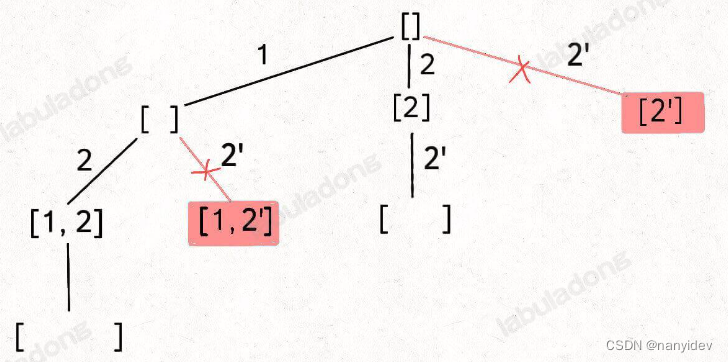
可以用[1,2,2’]来区分，通过画回溯树理解

在这里插入图片描述

5. lc78 子集

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集
输入：nums = [1,2,3]
输出：[ [],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3] ]

Solution：
与组合题目不同的是，求子集实际上求的是树的所有节点（而非叶子节点）

 List<List<Integer>> res  =new ArrayList<>();
 LinkedList<Integer> path = new LinkedList<>();
  public List<List<Integer>> subsets(int[] nums) {
      backTrack(nums,0);
      return res;

  }
  void backTrack(int[] nums,int startIndex)
  {
      // 注意这里是直接添加，因为要添加的是所有节点（而非前面题目的叶子节点）
      res.add(new ArrayList<>(path));

      // 终止条件可加可不加（因为下面的for循环结束回溯就结束了）
     /* if (startIndex >= nums.length){
          return;
      }*/

      for(int i=startIndex;i<nums.length;i++)
      {
          path.add(nums[i]);
          backTrack(nums,i+1);
          path.removeLast();
      }
  }

6. lc90 子集II

力扣90链接

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集
输入：nums = [1,2,2] 输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

Solution：
对比上题可以看出，这里需要考虑去重，所以与lc40 组合总和II 基本相同

    class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        dfs(nums,n,0);
        return res;
    }
    public void dfs(int[] nums,int n,int startIndex)
    {
        res.add(new LinkedList<>(path));

        for(int i=startIndex;i<n;i++)
        {
            if(i>startIndex && nums[i]==nums[i-1])
              continue;

            path.add(nums[i]);
            dfs(nums,n,i+1);
            path.removeLast();
        }
    }
}

排列

1. 全排列I

力扣46链接

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Solution：
终于来到排列了，排列和子集以及组合最大的不同就是排列可以位置不同，直接点，不需要startIndex！因为抽象成一个回溯树时，搜索起点只要没被选过就都可以，例如[1,2,3]选1，还剩[2,3],然后[1,2,3]选2，还剩[1,3]，这时肯定就不用startIndex，而是直接for循环从0索引开始。
但这时又有个问题，你怎么知道选过的元素，如果知道的话，直接跳过就好了，所以used数组应运而生，标记一下哪些元素用过了。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        int[] used = new int[nums.length]; // 也可以用bool类型
        Arrays.fill(used,0); // 0代表元素没有使用过
        dfs(nums,used);
        return res;
    }
    public void dfs(int[] nums,int[] used)
    {
        
        if(path.size()==nums.length)
        {
            res.add(new LinkedList<>(path));
            return;
        }
        for(int i=0;i<nums.length;i++)
        {
            // 注意这里的去重，佛如、循环只会傻傻的从头遍历，但是有些元素已经访问过了，直接跳过
            if(used[i]==1) continue;
            
            path.add(nums[i]);
            used[i]=1; // 用过了要记得标记一下哦！
            dfs(nums,used);
            used[i] = 0; // 回溯之后要还原
            path.removeLast();
        }
    }
}

2. 全排列II

力扣47链接

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列
输入：nums = [1,1,2]
输出：
[ [1,1,2],[1,2,1],[2,1,1] ]

Solution:
相比于上一题，又难了点。主要还是去重逻辑。联系上面的组合去重，肯定也可以排序＋相邻判断，另外还需要used数组，判断前一个元素是否被选择。为什么会多这一步呢？
当出现重复元素时，比如输入 nums = [1,2,2’,2’‘]，2’ 只有在 2 已经被使用的情况下才会被选择，同理，2’’ 只有在 2’ 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        int[] used = new int[nums.length];
        Arrays.fill(used,0);
        Arrays.sort(nums);
        dfs(nums,used);
        return res;

    }
     public void dfs(int[] nums,int[] used)
    {
        if(path.size()==nums.length)
        {
            res.add(new LinkedList<>(path));
            return;
        }
        for(int i=0;i<nums.length;i++)
        {
            if(used[i]==1) continue;

            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1]==0) {
                continue;
                }
            path.add(nums[i]);
            used[i]=1;
            dfs(nums,used);
            used[i] = 0;
            path.removeLast();
        }
    }
}

组合问题的应用

1.lc17 电话号码的字母组合

lc17 链接

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合
输入：digits = “23” 输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

Solution:
与组合问题最大的区别在于结果集来自“不同的组合”
首先需要建立一个映射，从字符2-9映射到字母，可以hash可以数组。注意本题的回溯树，第一层是第一个数字对应的字母。第二层是第一二数字对应的字母（有几个数字就有几层—深度），树的宽度却取决于数字对应的字母长度。

class Solution {
    List<String> res = new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        if(digits.length()==0) return res;
        String[] map = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        dfs(map,digits,0);
        return res;

    }
    StringBuilder sb = new StringBuilder();
    public void dfs(String[] map,String s,int index)
    {
        if(sb.length()==s.length())
        {
             res.add(sb.toString());
             return;
        }
        int digit = s.charAt(index)-'0'; // 对应的数字
        String str = map[digit];
        for(int i=0;i<str.length();i++)
        {
            sb.append(str.charAt(i));
            dfs(map,s,index+1);
            sb.deleteCharAt(sb.length()-1);
        }
        }   
}

2.lc131 分割回文串

描述：

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。
回文串是正着读和反着读都一样的字符串

示例：

输入：s = “aab”
输出：[[“a”,“a”,“b”],[“aa”,“b”]]

Solution：

List<List<String>> res = new ArrayList<>();
LinkedList<String> path = new LinkedList<>();

public List<List<String>> partition(String s) {
        backTrack(s,0);
        return res;
}

 void backTrack(String s,int index)
    {
        // 终止条件
        if(index >= s.length())
        {
            res.add(new ArrayList<>(path));
            return;
        }

        for(int i=index;i<s.length();i++)
        {
            if(isPalindrome(s,index,i))
            {
                String str = s.substring(index,i+1);
                path.add(str);
            }
            else
            continue;

            backTrack(s,i+1);
            path.removeLast();
        }
 }
 
// 判断是否是回文，用双指针的方法
boolean isPalindrome(String s, int start, int end)
    {
        while(start <=end)
        {
            if(s.charAt(start)!=s.charAt(end))
            {
                return false;
            }
            start++;
            end--;
        }
        return true;
}