---

泊松概率分布显示了事件在固定周期或空间内发生的几率。 可以使用 Python 将此数据绘制为直方图，以观察事件的发生率。

分布是可以绘制在直方图或其他结构上以找到数据集的最佳拟合曲线的曲线。 本文将教您如何使用 Python 在数据集上拟合泊松分布。

---

在 Python 中将泊松分布拟合到不同的数据集

让我们了解如何使用 SciPy 和 Python 在一组数据上绘制多个分布并拟合泊松分布。

---

在 Python 中拟合泊松分布的分箱最小二乘法

在此示例中，创建了一个虚拟泊松数据集，并使用该数据绘制了一个直方图。 绘制直方图后，分箱最小二乘法在直方图上拟合一条曲线以拟合泊松分布。

程序的导入函数

该程序使用以下导入函数。

1. Matplotlib 的数学分支——Numpy。
2. 用于绘制图表的 Matplotlib 子库 Pyplot。
3. SciPy curve_fit 用于导入曲线拟合。
4. 数据集的泊松。

为泊松分布创建一个虚拟数据集并使用该数据集绘制直方图

通过使用函数 np.random.poisson() ，使用 4-20,000 范围内的泊松偏差数创建变量 dataset_size。 它返回一个具有随机泊松值的数组。

data_set = np.random.poisson(4, 2000)

直方图数据的差异存储在新变量 bin 中。 它使用 np.arrange() 函数返回一个数组，其值介于 -0.5 到 20 之间，平均差为 0.5。

bins = np.arange(20) - 0.5

使用 plt.hist() 函数绘制直方图，其中参数为：

1. data_set 用于所使用的数据。
2. 差异的垃圾箱。
3. 密度，设置为真。
4. label，它向绘图添加标签。

在绘制直方图时，从 plt.hist() 函数返回三个值，这些值存储在三个新变量中 - 直方图 bin 值的条目、bin 边缘的 bin_edges 和直方图的各个补丁的补丁。

entries, bin_edges, patches = plt.hist(data_set, bins=bins, density=True, label='Data')

使用曲线拟合将曲线拟合到直方图

绘制直方图后，曲线拟合函数用于将泊松分布拟合到数据。 曲线函数绘制分散数据集中的最佳拟合线。

曲线拟合需要一个拟合函数，该函数将值数组转换为泊松分布，并将其作为参数返回，以在其上绘制曲线。 方法 fit_function 是用两个参数 k 和 parameters 创建的。

SciPy 库 poisson.pmf 用于获取参数。 pmf 代表概率质量函数，该函数返回随机分布的频率。

变量 k 存储事件发生的次数，变量 lamb 是用作曲线函数的拟合参数的 popt（减少平方和）。

SciPy curve_fit 函数接受三个参数，fit_function、middle_bins 和 entries，并返回两个值 - parameters（减少残差平方和的最佳值）和 cov_matrix（参数估计的协方差）。

parameters, cov_matrix = curve_fit(fit_function, middles_bins, entries)

创建一个包含 15 个递增值的数据集来绘制曲线，并使用 fit_function 方法拟合这些递增值的泊松分布。 提供了绘图的属性，并显示了结果。

x_plot = np.arange(0, 15)

plt.plot(
    x_plot,
    fit_function(x_plot, *parameters),
    marker='D', linestyle='-',
    color='red',
    label='Fit result',
)

完整代码:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.stats import poisson

# get random numbers that are poisson deviated
data_set = np.random.poisson(4, 2000)

# the bins have to be kept as a positive integer because poisson is a positive integer distribution
bins = np.arange(20) - 0.5
entries, bin_edges, patches = plt.hist(data_set, bins=bins, density=True, label='Data')

# calculate bin centers
middles_bins = (bin_edges[1:] + bin_edges[:-1]) * 0.5


def fit_function(k, lamb):
    # The parameter lamb will be used as the fit parameter
    return poisson.pmf(k, lamb)


# fit with curve_fit
parameters, cov_matrix = curve_fit(fit_function, middles_bins, entries)

# plot poisson-deviation with fitted parameter
x_plot = np.arange(0, 15)

plt.plot(
    x_plot,
    fit_function(x_plot, *parameters),
    marker='D', linestyle='-',
    color='red',
    label='Fit result',
)
plt.legend()
plt.show()

输出:

---

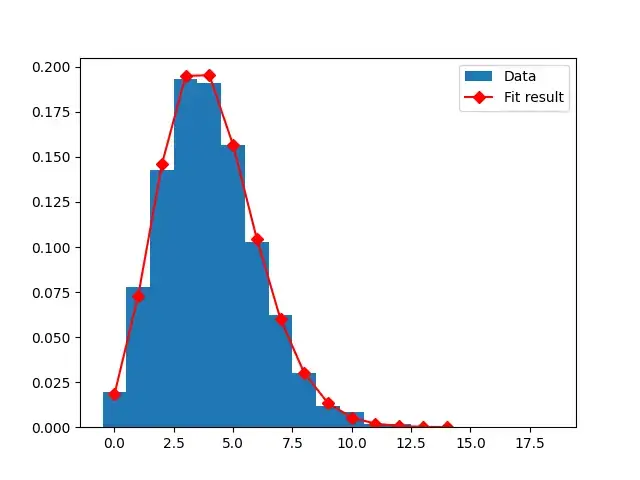
使用负二项式拟合过度分散的数据集上的泊松分布

在这个例子中，泊松分布数据框是用高度分散的数据创建的，我们将学习如何使泊松分布适合这个数据。

与上一个示例不同，泊松分布以其均值为中心，此数据高度分散，因此下一节将向此数据添加负二项式以改进泊松分布。

创建数据集

在此示例中，创建了一个 Pandas 数据框并将其存储在变量数据集中。 该数据集只有一列，出现次数为 2000 泊松值，lambda 值设置为 200。

dataset = pd.DataFrame({'Occurrence': np.random.poisson(200, 2000)})

使用数据集绘制直方图

要绘制直方图，我们需要提供三个值，bin 的间隔（值桶）、bin 的起点和 bin 的终点。 这是通过以下方式完成的：

width_of_bin = 15
xstart = 150
xend = 280
bins = np.arange(xstart, xend, width_of_bin)

设置 bins 的值后，绘制直方图。

hist = sns.histplot(data=dataset["Occurrence"], kde=True, bins=bins)

将泊松分布曲线拟合到直方图

通过绘制分布曲线，需要数据集的均值和大小来拟合泊松分布。 在两个新变量 mu 和 n 中，分别存储了数据集的均值和大小。

绘制泊松分布曲线的算法是：

bins + width_of_bin / 2, n * (poisson.cdf(bins + width_of_bin, mu) - poisson.cdf(bins, mu))

最后，曲线绘制在直方图上。

完整代码：

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import poisson

dataset = pd.DataFrame({'Occurrence': np.random.poisson(200, 2000)})

width_of_bin = 15
xstart = 150
xend = 280
bins = np.arange(xstart, xend, width_of_bin)

hist = sns.histplot(data=dataset["Occurrence"], kde=True, bins=bins)
mu = dataset["Occurrence"].mean()
n = len(dataset)
plt.plot(bins + width_of_bin / 2, n * (poisson.cdf(bins + width_of_bin, mu) - poisson.cdf(bins, mu)), color='red')
plt.show()

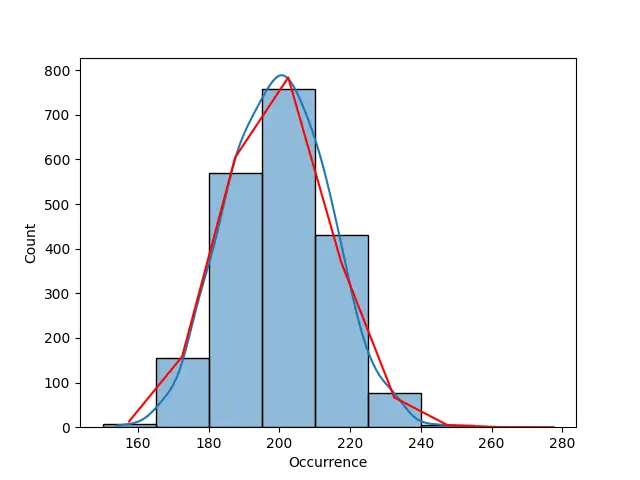
输出:

---

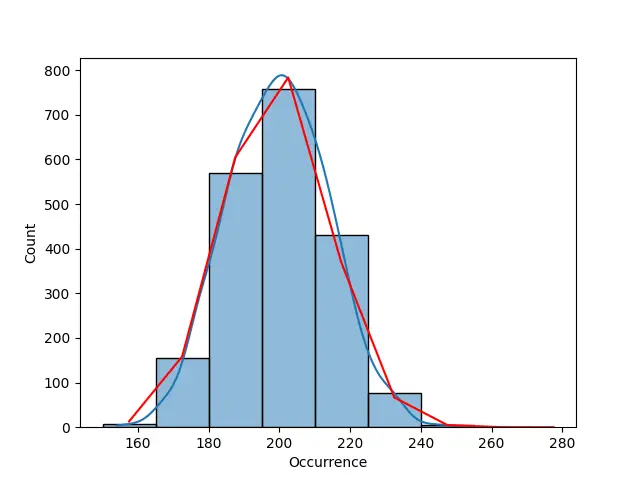
使用负二项分布的高度分散数据的泊松分布

如前所述，此数据集中的数据过于分散，这就是曲线与泊松分布曲线不完全相似的原因。 下面的示例中使用了负二项式来拟合泊松分布。

数据集是通过注入负二项式创建的：

dataset = pd.DataFrame({'Occurrence': nbinom.rvs(n=1, p=0.004, size=2000)})

直方图的 bin 从 0 开始，到 2000 结束，公共间隔为 100。

binwidth = 100
xstart = 0
xend = 2000
bins = np.arange(xstart, xend, binwidth)

创建 bin 和数据集后，绘制直方图：

hist = sns.histplot(data=dataset["Occurrence"], kde=True, bins=bins)

该曲线需要五个参数，方差（Var），均值（mu），p（均值/方差），r（考虑的项目）和n（数据集中的总项目）

方差和均值在两个变量中计算，方差和 mu。

Var = dataset["Occurrence"].var()
mu = dataset["Occurrence"].mean()

以下公式用于找出 p 和 r：

p = (mu / Var)
r = mu ** 2 / (Var - mu)

通过将数据集的长度保存在新变量 n 中来存储项目总数。

n = len(dataset)

最后，曲线绘制在直方图上。

plt.plot(bins + binwidth / 2, n * (nbinom.cdf(bins + binwidth, r, p) - nbinom.cdf(bins, r, p)))

完整代码:

import numpy as np
from scipy.stats import nbinom
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

dataset = pd.DataFrame({'Occurrence': nbinom.rvs(n=1, p=0.004, size=2000)})

binwidth = 100
xstart = 0
xend = 2000
bins = np.arange(xstart, xend, binwidth)

hist = sns.histplot(data=dataset["Occurrence"], kde=True, bins=bins)

Var = dataset["Occurrence"].var()
mu = dataset["Occurrence"].mean()
p = (mu / Var)
r = mu ** 2 / (Var - mu)
n = len(dataset)

plt.plot(bins + binwidth / 2,
         n * (nbinom.cdf(bins + binwidth, r, p) - nbinom.cdf(bins, r, p)),
         color='red')
plt.show()

输出:

---

总结

本文介绍了在 Python 中将泊松分布拟合到数据集的三种方法。 阅读本文后，读者可以在虚拟泊松数据集和过度分散的数据集上拟合泊松分布。