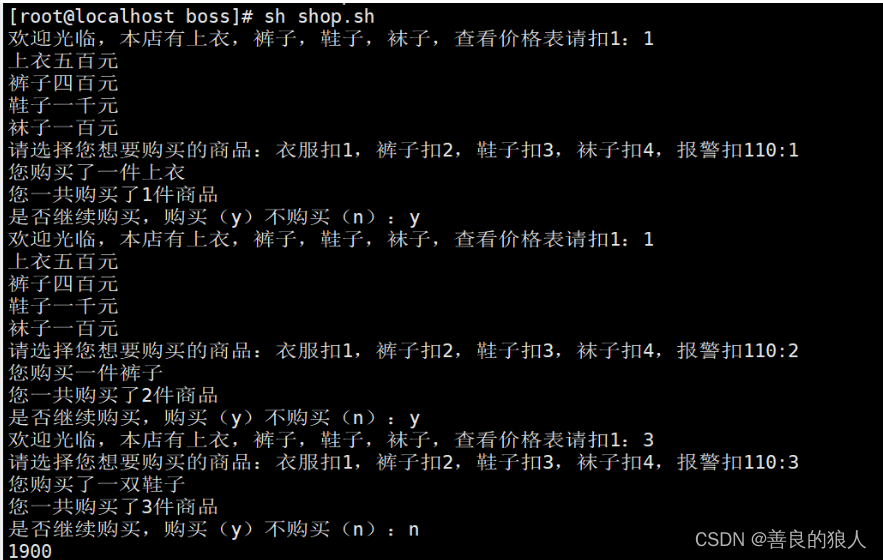
前向传播（Forward）

为什么要有激活函数

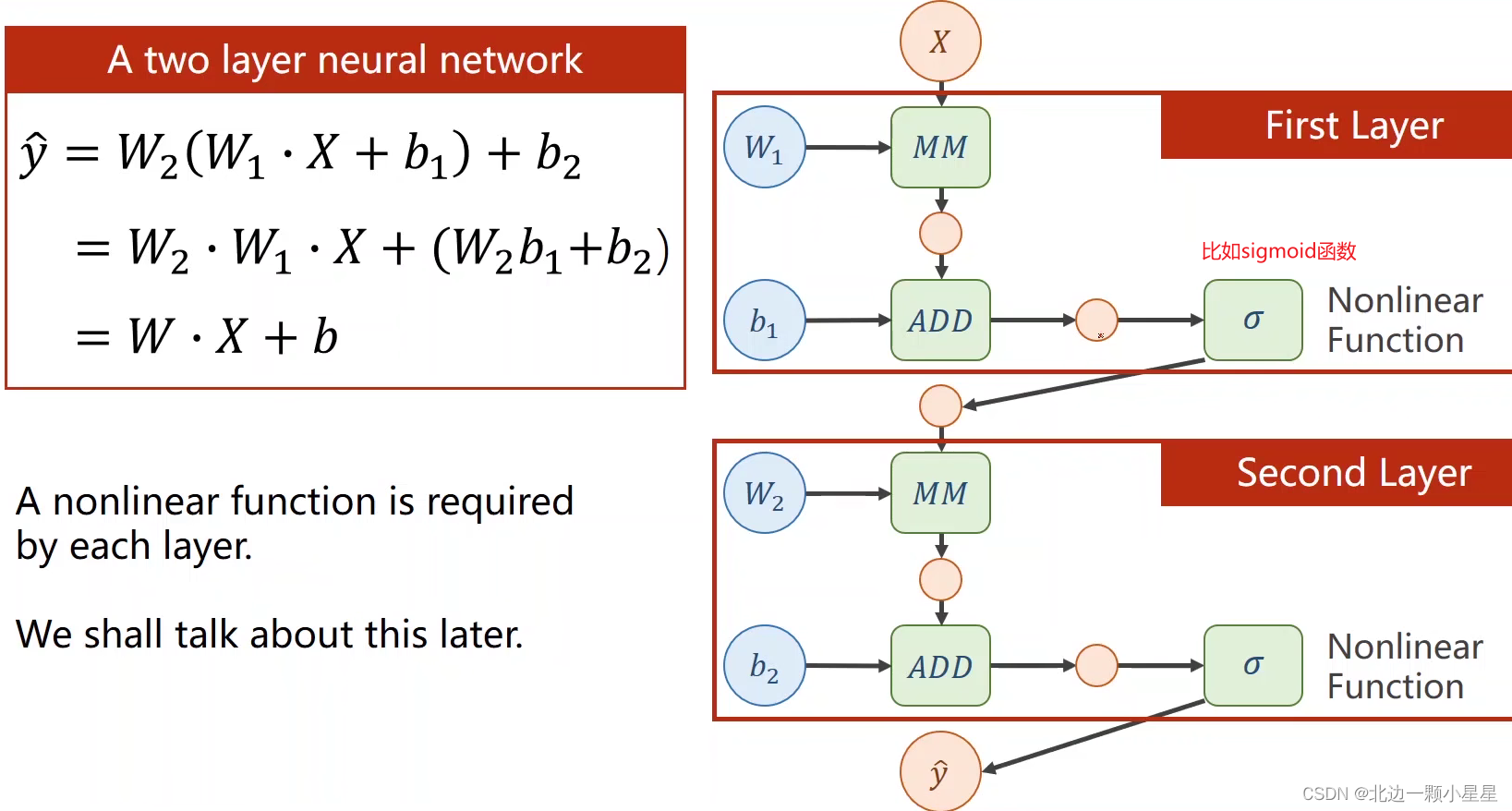
这里用两层来代表多层的神经网络举例：第一层的输出是第二层的输入，其中MM的W*X矩阵乘法，ADD是向量加法即加上偏置，如果每一层都只有线性变换，那么最终无论多少层都可以化简成一层（见上图左边的公式），这样多层数就没有意义了，所以要在每一层都加上非线性函数即激活函数，才能保证每一层都有它独特的作用。

 

链式法则 

 

 

 

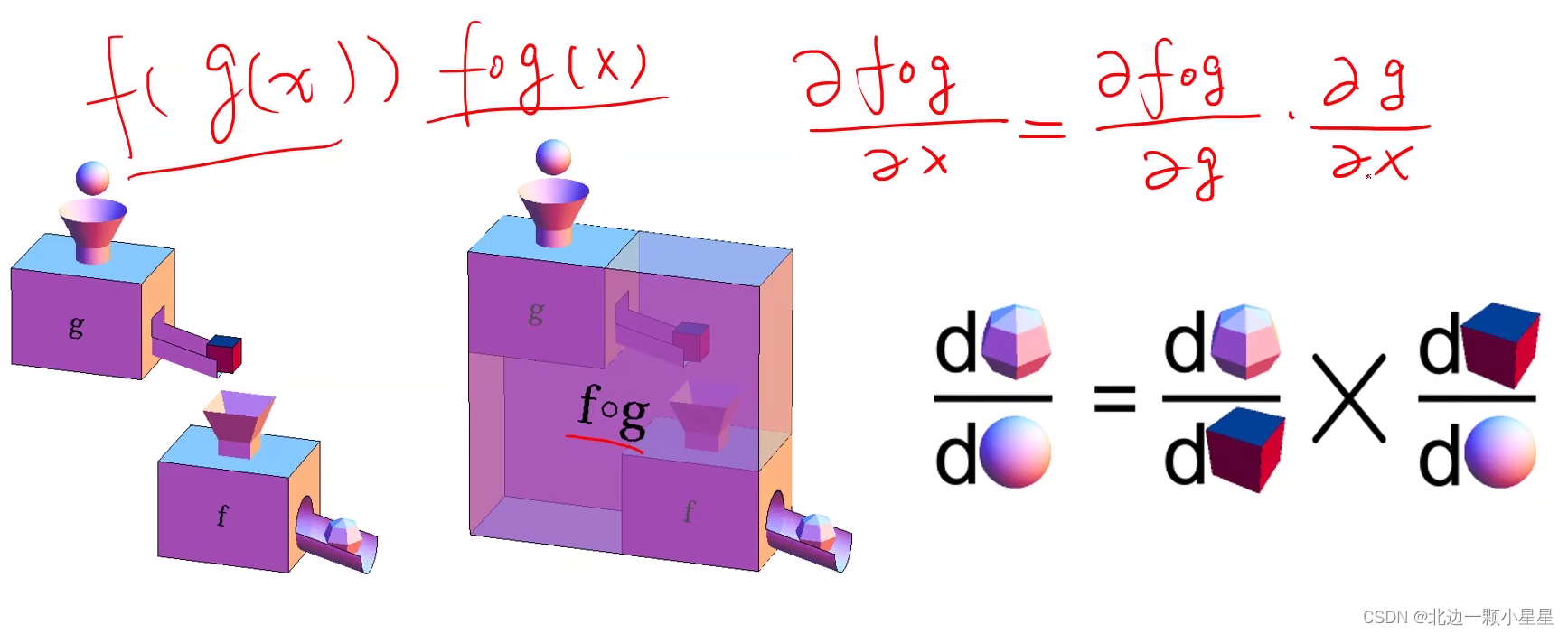
反向传播（Backward） 

  

当x是上一层的输出时也需要算，它这时就相当于是上一层的输出z一样。

损失L对z的偏导是从后面反向传播时传过来的，z对x的偏导是前面做前向传播时计算f这个函数时算出来的局部梯度。

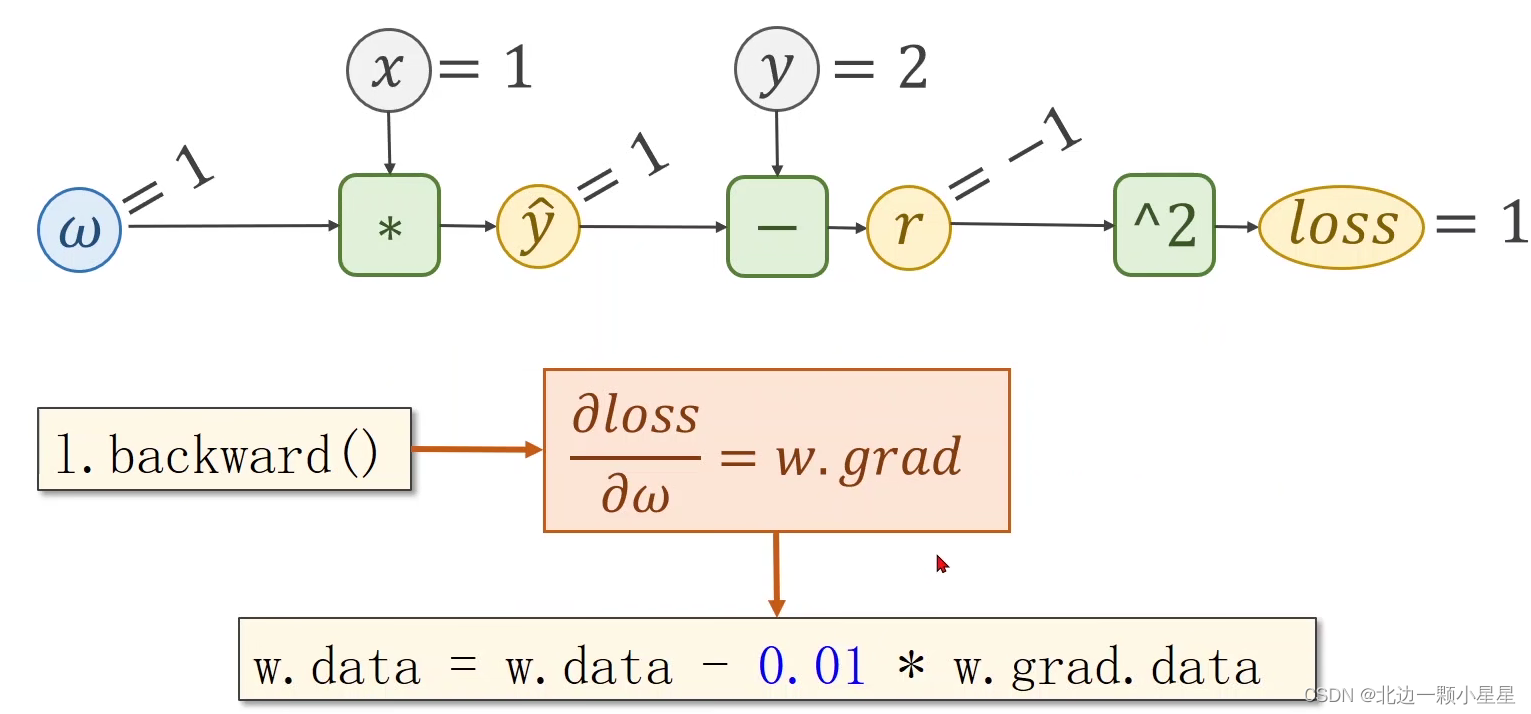
下面举个具体例子：

比如在前向传播中，函数f=x*w，那么z对x的偏导为w，z对w的偏导为x，当传入的x=2，w=3时，输出z=x*w=6。

然后在反向传播中，我们拿到损失Loss，计算出L对z的偏导为5，接着计算出L对x的偏导为5*w即5*3=15，同理L对w的偏导为10，然后L对x的偏导的结果再继续往上一层传，这样每一层都通过对w的偏导就可以由此做权重w的更新了。

上面是前向和反向的整体流程，计算出loss对w的偏导就可以用梯度下降算法对w进行更新了。

 

上面是梯度下降算法的公式推导。

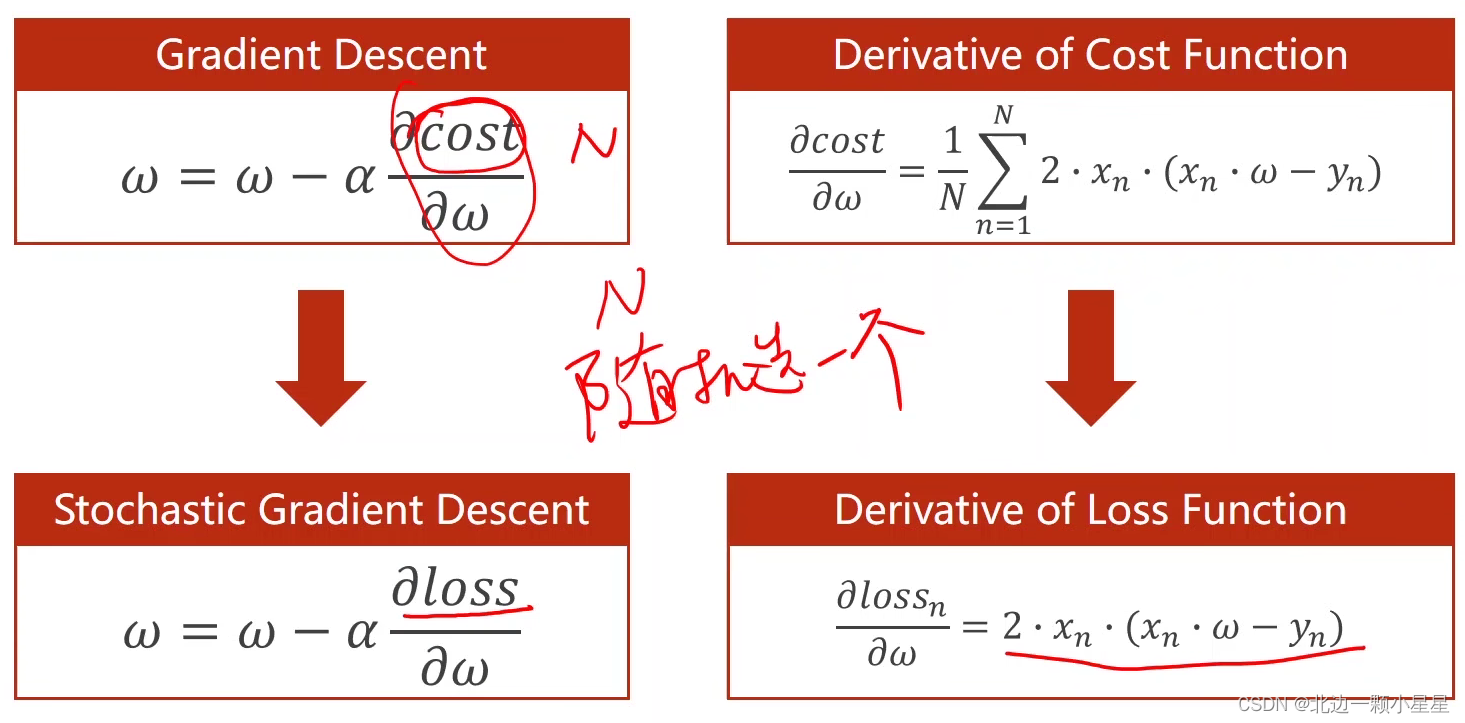
上面这个是随机梯度下降算法的公式。 

代码演示：