机器学习决策树、回归树 sklearn-day1

#文章很多内容来自菜菜老师的课件。仅做笔记

一、决策树

1、模块
树模块
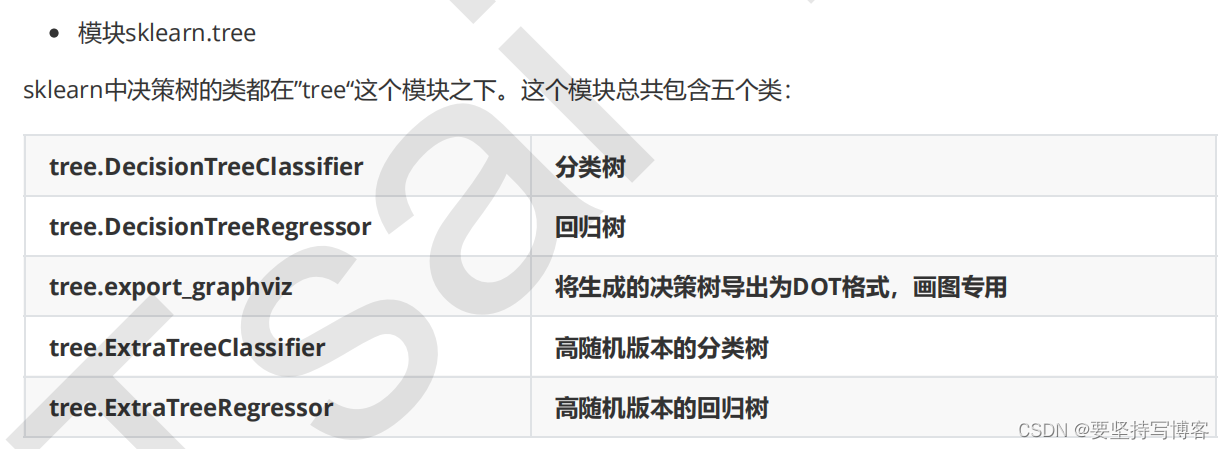
2、sklearn基本建模流程

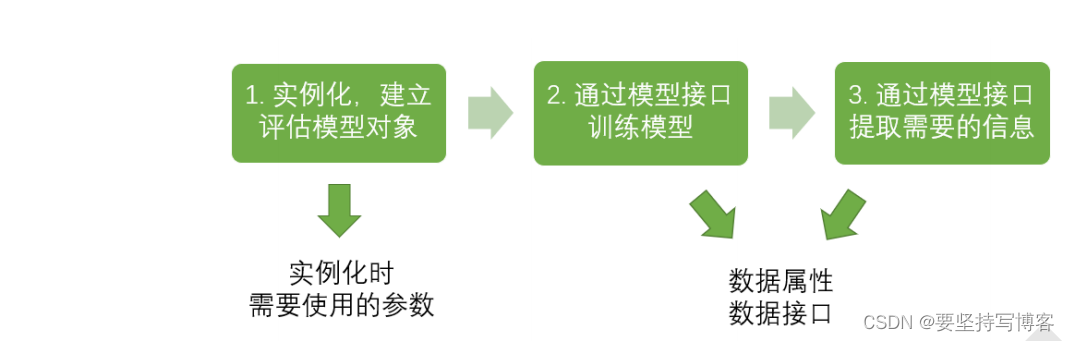
#分类树对应的代码
from sklearn import tree #导入需要的模块
clf = tree.DecisionTreeClassifier()     #实例化
clf = clf.fit(X_train,y_train) #用训练集数据训练模型
result = clf.score(X_test,y_test) #导入测试集，从接口中调用需要的信息

其中sklearn分类树对应的参数如下：

class sklearn.tree.DecisionTreeClassifier (criterion=’gini’, splitter=’best’, max_depth=None,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None,
class_weight=None, presort=False)

其中criterion参数有entropy、gini（默认）。
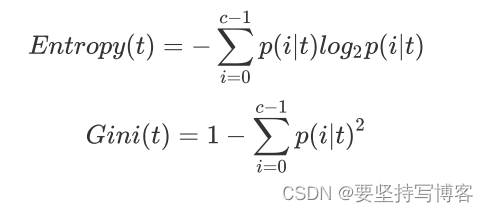
在这里插入图片描述
其中t代表给定的节点，i代表标签的任意分类， $p (i ∣ t)$ 代表标签分类i在节点t上所占的比例。注意，当使用信息熵时，sklearn实际计算的是基于信息熵的信息增益(Information Gain)，即父节点的信息熵和子节点的信息熵之差。
比起基尼系数，信息熵对不纯度更加敏感，对不纯度的惩罚最强。但是在实际使用中，信息熵和基尼系数的效果基本相同。信息熵的计算比基尼系数缓慢一些，因为基尼系数的计算不涉及对数。另外，因为信息熵对不纯度更加敏感，所以信息熵作为指标时，决策树的生长会更加“精细”，因此对于高维数据或者噪音很多的数据，信息熵很容易过拟合，基尼系数在这种情况下效果往往比较好。当然，这不是绝对的。

接下来就是上代码了。
建一棵树
1、导入需要的算法库和模块

from sklearn import tree
from sklearn.datasets import load_wine #红酒数据集
from sklearn.model_selection import train_test_split #能够将数据集按照用户的需要指定划分为训练集和测试集

2、探索数据

wine = load_wine()
wine.data.shape
wine.target

#如果wine是一张表，应该长这样：
import pandas as pd
pd.concat([pd.DataFrame(wine.data),pd.DataFrame(wine.target)],axis=1)

wine.feature_names
wine.target_names

3.分训练集和测试集

Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
# train_data：所要划分的样本特征集
# train_target：所要划分的样本结果
# test_size：样本占比，如果是整数的话就是样本的数量
# random_state：是随机数的种子。
# 随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。
Xtrain.shape
Xtest.shape

4.建立模型

clf = tree.DecisionTreeClassifier(criterion="entropy") #实例化
clf = clf.fit(Xtrain, Ytrain) #建模
score = clf.score(Xtest, Ytest) #返回预测的准确度
score

5.画一棵树

feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
import graphviz
dot_data = tree.export_graphviz(clf
                               ,feature_names= feature_name
                               ,class_names=["琴酒","雪莉","贝尔摩德"]
                               ,filled=True
                               ,rounded=True
                               )
graph = graphviz.Source(dot_data)

graph

6.探索决策树

#特征重要性
clf.feature_importances_

[*zip(feature_name,clf.feature_importances_)]

我们已经在只了解一个参数的情况下，建立了一棵完整的决策树。但是回到步骤4建立模型，score会在某个值附近波动，引起步骤5中画出来的每一棵树都不一样。它为什么会不稳定呢？如果使用其他数据集，它还会不稳定吗？
我们之前提到过，无论决策树模型如何进化，在分枝上的本质都还是追求某个不纯度相关的指标的优化，而正如我们提到的，不纯度是基于节点来计算的，也就是说，决策树在建树时，是靠优化节点来追求一棵优化的树，但最优的节点能够保证最优的树吗？集成算法被用来解决这个问题：sklearn表示，既然一棵树不能保证最优，那就建更多的不同的树，然后从中取最好的。怎样从一组数据集中建不同的树？在每次分枝时，不从使用全部特征，而是随机选取一部分特征，从中选取不纯度相关指标最优的作为分枝用的节点。这样，每次生成的树也就不同了。总结一下就是优化节点中的节点是具有随机性的，并不能让这个模型固定起来，所有有了上述步骤3解释的random_state这个参数，随机数种子。

clf = tree.DecisionTreeClassifier(criterion="entropy",random_state=30)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest) #返回预测的准确度

score

与random_state类似的参数有splitter。
splitter也是用来控制决策树中的随机选项的，有两种输入值，输入”best"，决策树在分枝时虽然随机，但是还是会优先选择更重要的特征进行分枝（重要性可以通过属性feature_importances_查看），输入“random"，决策树在分枝时会更加随机，树会因为含有更多的不必要信息而更深更大，并因这些不必要信息而降低对训练集的拟合。这也是防止过拟合的一种方式。当你预测到你的模型会过拟合，用这两个参数来帮助你降低树建成之后过拟合的可能性。当然，树一旦建成，我们依然是使用剪枝参数来防止过拟合。

#如下代码所示
clf = tree.DecisionTreeClassifier(criterion="entropy"
                                 ,random_state=30
                                 ,splitter="random"
                                 )
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
score

7.剪枝参数，**剪枝策略对决策树的影响巨大，正确的剪枝策略是优化
决策树算法的核心。**sklearn提供了以下剪枝策略：

max_depth:限制树的最大深度，超过设定深度的树枝全部剪掉
min_samples_leaf & min_samples_split: min_samples_leaf限定，一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个训练样本，否则分
枝就不会发生，或者，分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生。min_samples_split限定，一个节点必须要包含至少min_samples_split个训练样本，这个节点才允许被分枝。

clf = tree.DecisionTreeClassifier(criterion="entropy"
                                 ,random_state=30
                                 ,splitter="random"
                                 ,max_depth=3
                                 ,min_samples_leaf=10
                                 ,min_samples_split=10
                                 )
clf = clf.fit(Xtrain, Ytrain)
dot_data = tree.export_graphviz(clf
                               ,feature_names= feature_name
                               ,class_names=["琴酒","雪莉","贝尔摩德"]
                               ,filled=True
                               ,rounded=True
                               )  
graph = graphviz.Source(dot_data)
graph
clf.score(Xtrain,Ytrain)
clf.score(Xtest,Ytest)

max_features：max_features限制分枝时考虑的特征个数，超过限制个数的特征都会被舍弃。其方法比较暴力，是直接限制可以使用的特征数量
而强行使决策树停下的参数，在不知道决策树中的各个特征的重要性的情况下，强行设定这个参数可能会导致模型学习不足。如果希望通过降维的方式防止过拟合，建议使用PCA，ICA或者特征选择模块中的降维算法。

8.确认最优的剪枝参数
那具体怎么来确定每个参数填写什么值呢？这时候，我们就要使用确定超参数的曲线来进行判断了，继续使用我们已经训练好的决策树模型clf。超参数的学习曲线，是一条以超参数的取值为横坐标，模型的度量指标为纵坐标的曲线，它是用来衡量不同超参数取值下模型的表现的线。在我们建好的决策树里，我们的模型度量指标就是score。

import matplotlib.pyplot as plt
test = []
for i in range(10):
    clf = tree.DecisionTreeClassifier(max_depth=i+1
                                     ,criterion="entropy"
                                     ,random_state=30
                                     ,splitter="random"
                                     )
    clf = clf.fit(Xtrain, Ytrain)
    score = clf.score(Xtest, Ytest)
    test.append(score)
plt.plot(range(1,11),test,color="red",label="max_depth")
plt.legend()
plt.show()

9.目标权重参数：
截图课件的
10.重要属性和接口

#apply返回每个测试样本所在的叶子节点的索引
clf.apply(Xtest)
#predict返回每个测试样本的分类/回归结果
clf.predict(Xtest)

参数、属性和接口均如下所示：在这里插入图片描述

二、回归树

回归树使用最大均方差划分节点；每个节点样本的均值作为测试样本的回归预测值。
回归树案例：

import numpy as np #生成图像数据点的
from sklearn.tree import DecisionTreeRegressor #回归树
import matplotlib.pyplot as plt #画图的

rng = np.random.RandomState(1) #随机数种子
X = np.sort(5 * rng.rand(80,1),axis = 0) #rand(80，1)生成随机数80行，1列 
y = np.sin(X).ravel() #降维，生成正弦曲线
#画图
# plt.figure()
# plt.scatter(X,y,s=20,edgecolor="black",c="darkorange",label="data")
y[::5] += 3*(0.5 - rng.rand(16)) #加上噪声，也就是把数据有小幅度变化（y[::5]每行每列间隔5）
#np.random.rand(数组结构)，生成随机数组函数
#降维函数ravel()的用法
#np.random.random((2,1))
#下图是没有加噪声的

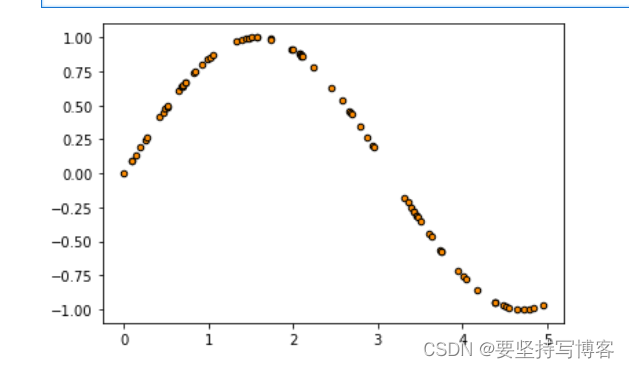
在这里插入图片描述

regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X,y)
regr_2.fit(X,y)

X_test = np.arange(0.0,5.0,0.01)[:,np.newaxis]
#arange是生成有序的数列
#[:,np.newaxis]升维 ， 比如变成4行1列。[np.newaxis，：]这就变成1行4列
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)

plt.figure()
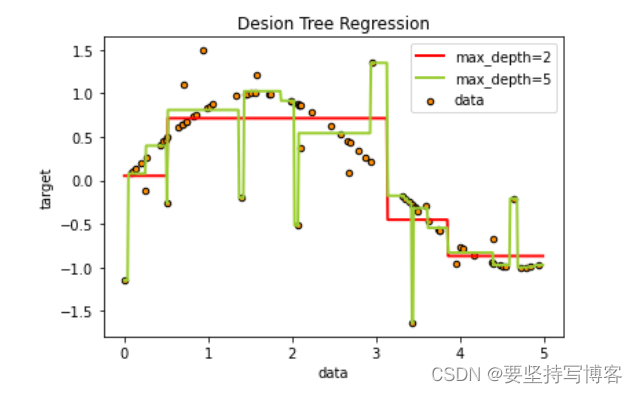
plt.scatter(X,y,s=20,edgecolor="black",c="darkorange",label="data") #c是点的颜色 s是点的大小
plt.plot(X_test,y_1,color="red",label="max_depth=2",linewidth=2)
plt.plot(X_test,y_2,color="yellowgreen",label="max_depth=5",linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Desion Tree Regression")
plt.legend()
plt.show()
#结果图如下所示