一.中缀表达式转后缀表达式
初始化一个栈,用于保存 暂时还不确定的运算顺序的“运算符” 。
从 左往右 依次扫描,会遇到三种情况:
1.遇到 操作数,直接加入后缀表达。
2.遇到 界限符:
①遇到 “(” 入栈。
②遇到 “)” 依次弹出栈内运算符并加入后缀表达式,直到弹出 "("为止。(注: “(” 不加入后缀表达式)
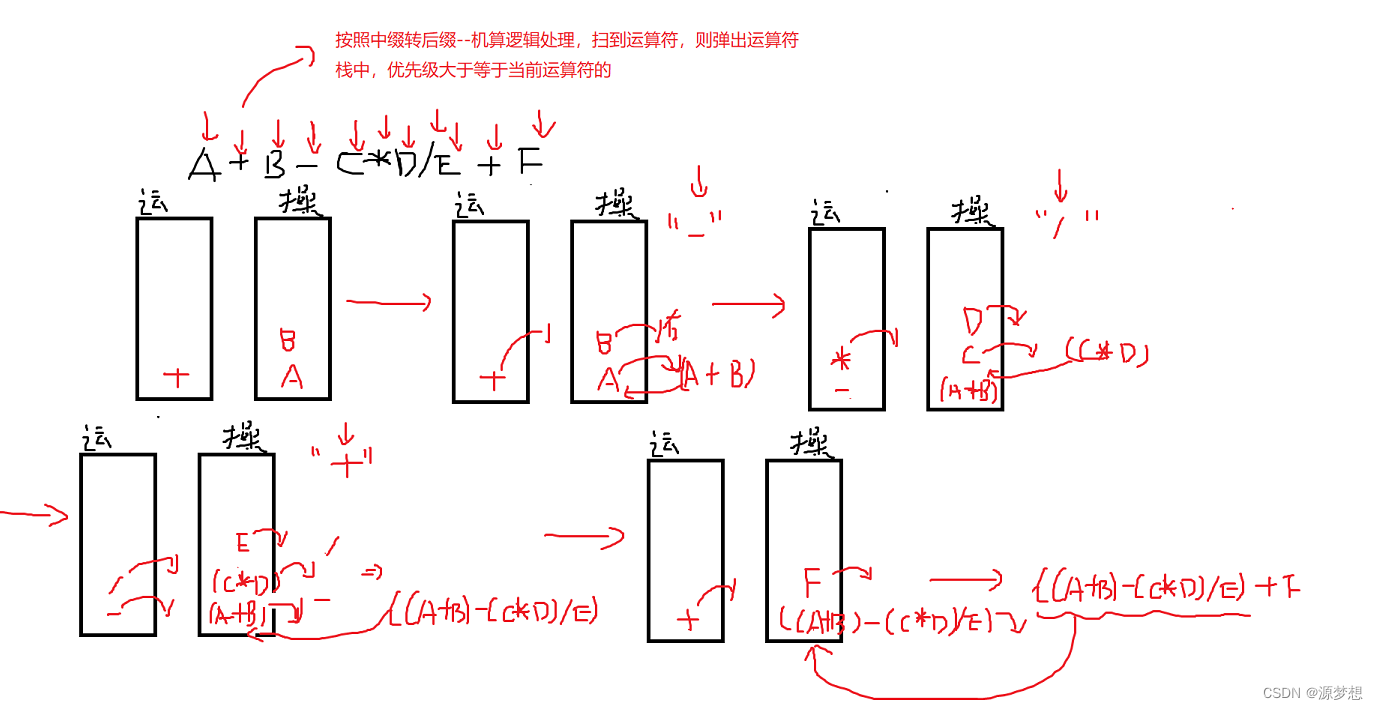
3.遇到 运算符 依次弹出栈中优先级 高于或等于 当前运算符的所有运算符,并且加入后缀表达式中,直到碰到 “(” 或者 栈空为止。
注:处理完所有字符后,将栈中剩下的运算符依次弹出,并加入后缀表达式。
1.某些地方的解释
①依次弹出栈中优先级 高于或等于 当前运算符的所有运算符
在中缀表达式中,除了第一个与最后一个操作数外,每个操作数左右都会有运算符。我们是从左往右扫描:当我们扫到操作数的 左运算符时,由于不知 右运算符,故不知左右生效顺序,继续扫描
当我们扫到 右运算符后:
①若右运算符优先级低于或等于 左运算符 (即栈中优先级高于或等于当前扫到的运算符)根据“左优先”原则,我们可以确定,先让左边运算符生效,(即弹出所有优先级大于等于当前的运算符)
②若右运算符优先级高于栈中左边运算符优先级,则加入栈中,依然无法确定生效顺序,因为相对于下一个操作数的右运算符来说,当前运算符相当于左运算符,由于不知道下一个操作数的右运算符,所以当前确定不了生效顺序,只好先入栈。
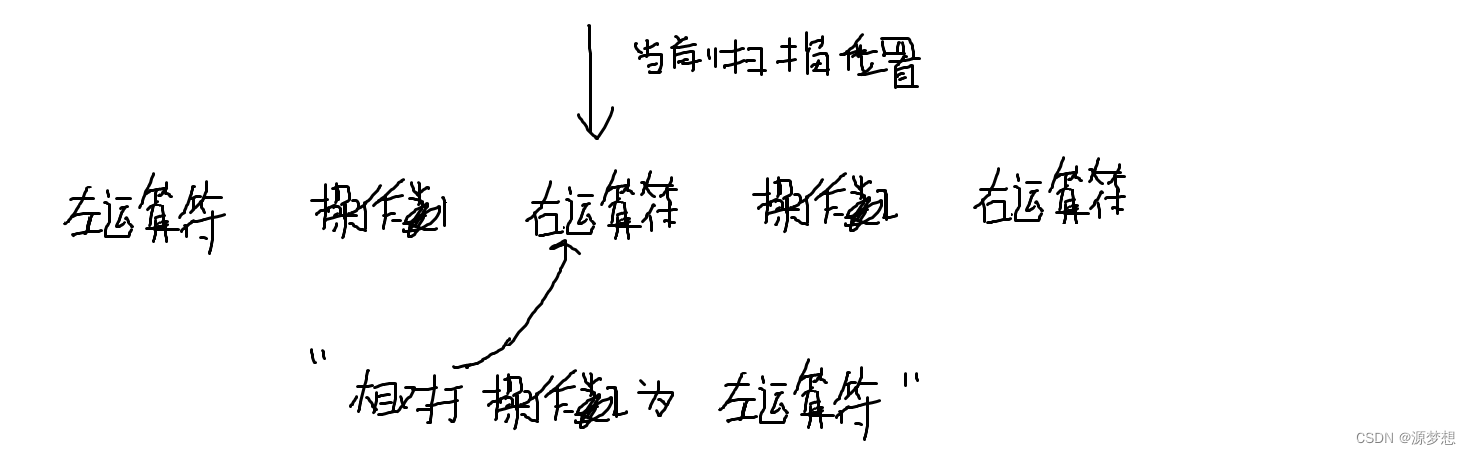
②直到碰到 “(” 或者 栈空为止
这个规则,只有在含有两层以上 " ( ) " 才会触发。
我们可以把 " ( ) "内的表达式 看成一个独立的子式,其规则与主式一样,两者生效顺序互不影响。
③遇到 “)” 依次弹出栈内运算符并加入后缀表达式
当遇到了 “)” 我们就确定了 这个 括号的范围, 那么我们就可以让括号内的先生效。
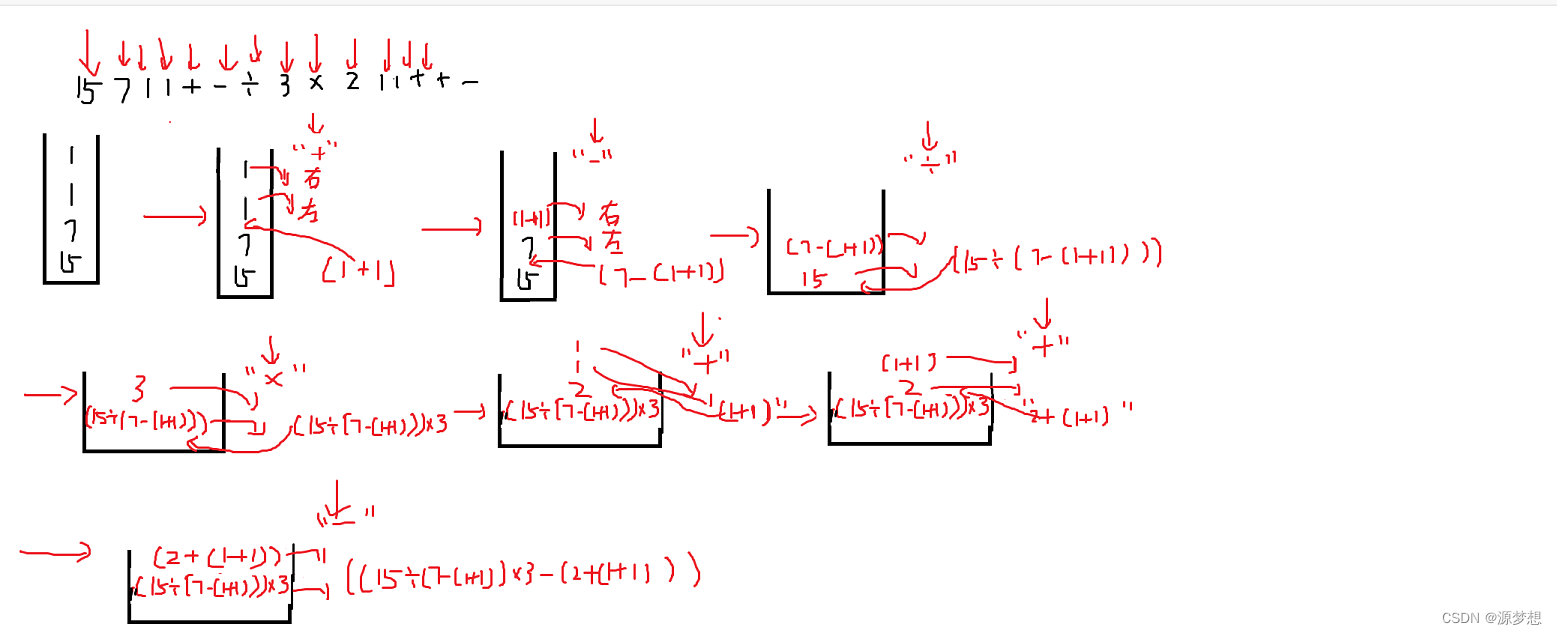
2.机算过程
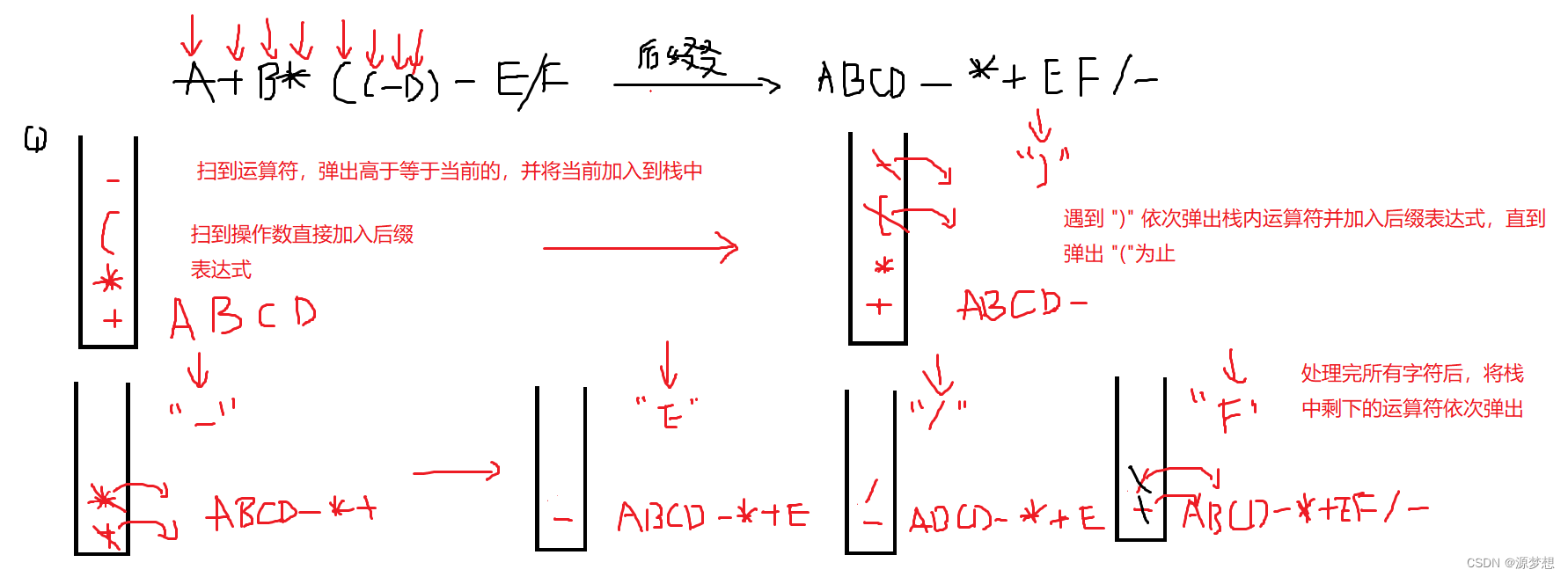
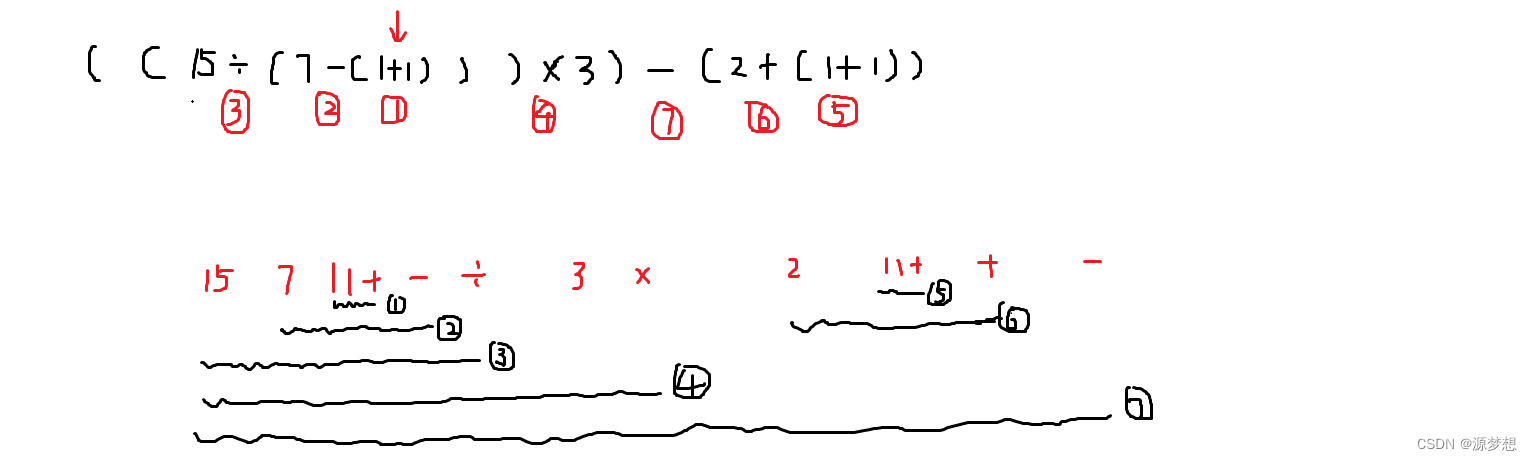
3.手算模拟
第一步:确定运算符生效顺序
第二步:选择下一个运算符,按<左操作数 ,右操作数 , 运算符 >的顺序组成一个新的操作数。直至处理完所有。
王道给出左优先原则,若两个运算符可以同时生效,则为了保证算法的确定性,可先让左边的运算符生效。
注:左优先不是术语,考试要详细叙述。
三.计算后缀表达式
1.机算
1,从左往右扫描下一个元素,直到处理完所有元素
2.若扫描到 操作数 则入栈并继续 1
若扫描到 运算符 则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶 继续 1.
注:先出栈的为右操作数。
2.手算
略
四.中缀表达式的计算(中缀转后缀算法+后缀表达式计算算法)
初始化两个栈:操作数栈 和 运算符栈
1.若扫描到操作数,压入操作数栈
2.若扫描到运算符 或 界限符,则按照 “中缀转后缀–机算” 相同的逻辑压入运算符栈
(期间也会弹出运算符,每弹出一个运算符时,就需要弹出两个操作数栈的栈顶元素,并执行相应运算,运算结果再压回操作数栈)
五.其他
1.中缀转前缀时,手算与中缀转后缀区别:
①确定运算顺序
②选择下一个运算符,按<运算符 , 左操作数 , 右操作数> 组成一个新的操作数,直到处理完毕。
2.中缀转前缀时,机算与中缀转后缀区别:
①从右往左扫描
②先出栈的为“左操作数”
3.后缀转中缀
略