记录一下我看过的利用CNN实现知识推理的论文。

最后修改时间：2023.05.08

目录

1.ConvE

1.1.解决的问题

1.2.优势

1.3.贡献与创新点

1.4.方法

1.4.1 为什么用二维卷积，而不是一维卷积？

1.4.2.ConvE具体实现

---

1.ConvE

论文：Convolutional 2D Knowledge Graph Embeddings

会议/期刊：

1.1.解决的问题

（1）以往的模型都太浅了，虽然可以快速用于大型数据集，但是学到的特征表达能力比较差；

（2）另一个比较严重的问题是数据集的泄露问题“test set leakage”，也就是训练集出现过的关系三元组，取了反后，在测试集中又出现了一遍。比如，(A,妈妈,B)在训练集中出现过，(B,女儿,A)又在测试集中出现。这个问题导致一些很简单的rule-based模型也可以达到很好的效果。

1.2.优势

（1）采用多层神经网络，特征表达能力强；

（2）参数量很少，相同的实验效果，参数量比DistMult少8倍，比R-GCN少17倍；

（3）可以高效建模大型数据集常出现的入度高的节点。

1.3.贡献与创新点

（1）设计2D卷积模型，进行链接预测；

（2）设计1-N scoring步骤，提升训练和评估的速度；

（3）参数量少；

（4）随着知识图谱复杂性的提升，ConvE与一些shallow算法的差距成比例增大；

（5）分析了各数据集泄露的问题，并提出了不泄露的版本；

（6）sota。

1.4.方法

1.4.1 为什么用二维卷积，而不是一维卷积？

       NLP任务中大多采用的是一维卷积，包括下面要提到的ConvKB算法，但是ConvE却创新的使用了二维卷积。因为二维卷积使得嵌入向量间的交互点变多了，模型的表达能力变强。举个栗子~

一维卷积：

两个一维嵌入分别为和，两个嵌入concat后得到向量。

一维卷积核大小为3，那么卷积的过程中，两个向量只有连接点处的值（比如或）发生了交互，并且交互程度会随着卷积核大小的增加而变深。

二维卷积：

两个二维嵌入分别为和，两个嵌入concat后得到嵌入。

二维卷积核大小为3×3，卷积的过程中，卷积核可以建模concat边界线处的交互，特征交互更多。

换一个模式（将嵌入的几行调换一下位置），得到，那么可以发现交互的点更多了。

1.4.2.ConvE具体实现

        链接预测算法一般由编码模块和打分模块构成，编码模块负责得到实体和关系的嵌入向量，打分模块负责为三元组打分。

        ConvE由卷积层和全连接层构成。

下面是ConvE的算法流程图：

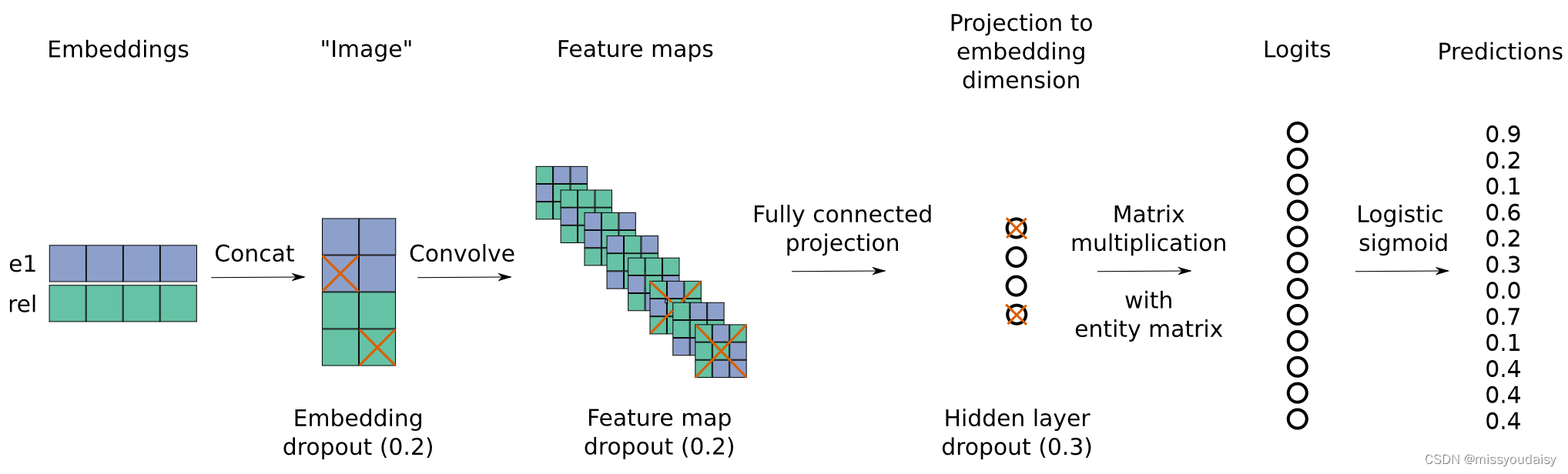
步骤：（可结合上图食用~）

（1）在所有的实体和关系的嵌入矩阵中，查找当前计算的实体和关系的嵌入向量和；

（2）对嵌入向量做2D的reshape，得到嵌入矩阵和，维度从变为；

（3）concat嵌入矩阵和，并将结果作为卷积的输入，输出个的特征图；

（4）将特征图reshape成的向量，并利用全连接层将向量映射为维；

（5）然后将该向量与实体嵌入向量做内积，进行匹配，得到分数。这里涉及到1-N scoring，后面会讲到。

（6）为了训练，对分数进行logistic sigmoid函数计算，得到最终分数。

打分函数：

        是ReLU激活函数。

损失函数：

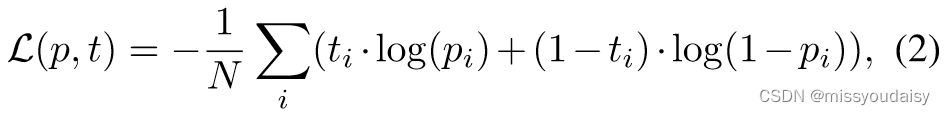
        如果三元组存在，为1，否则，为0。最小化损失函数。

Dropout：

        作者还使用了很多种dropout手段，包括对嵌入矩阵、卷积后的特征图和全连接层后的输出进行不同概率的dropout。

1.4.3.1-N scoring