使用PyTorch构建神经网络，并计算参数Params

文章目录

- 使用PyTorch构建神经网络，并计算参数Params
- 举例
- - 计算具有全连接层的神经网络的参数数量
  - 计算卷积神经网络的参数数量
  - - Params计算过程
- 总结

使用PyTorch构建神经网络，并计算参数Params

在深度学习中，模型的参数数量是一个非常重要的指标，通常会影响模型的大小、训练速度和准确度等多个方面。在本教程中，我们将介绍如何计算深度学习模型的参数数量。

本教程将以PyTorch为例，展示如何计算一个包含卷积、池化、归一化和全连接等多种层的卷积神经网络的参数数量。具体来说，我们将首先介绍一个具有全连接层的神经网络的参数计算方法，然后扩展到包含卷积、池化、归一化和全连接等多种层的卷积神经网络。

举例

计算具有全连接层的神经网络的参数数量

假设我们有一个输入向量 $x$ ，其维度为 $d_{in}$ ，我们想将其映射到一个输出向量 $y$ ，其维度为 $d_{out}$ 。我们可以使用一个具有 $n$ 个隐藏层的全连接神经网络来完成这个映射，其中每个隐藏层具有 $h$ 个神经元。

在PyTorch中，我们可以通过定义一个继承自nn.Module的类来实现这个神经网络。下面是一个定义了一个具有两个隐藏层的全连接神经网络的示例代码：

import torch
import torch.nn as nn

class Net(nn.Module):
    def __init__(self, d_in, h, d_out, n):
        super(Net, self).__init__()
        self.linear1 = nn.Linear(d_in, h)
        self.linear2 = nn.Linear(h, h)
        self.linear3 = nn.Linear(h, d_out)
        self.n = n

    def forward(self, x):
        h_relu = self.linear1(x).clamp(min=0)
        for i in range(self.n):
            h_relu = self.linear2(h_relu).clamp(min=0)
        y_pred = self.linear3(h_relu)
        return y_pred

其中，nn.Linear是PyTorch中的一个线性层，它将输入向量乘以一个权重矩阵，并加上一个偏置向量，得到输出向量。在这个例子中，我们定义了三个线性层，分别为self.linear1、self.linear2和self.linear3。在forward函数中，我们首先将输入向量x传递给self.linear1，然后通过ReLU非线性激活函数得到一个隐藏层输出h_relu。接下来，我们使用for循环多次将h_relu传递给self.linear2，再次使用ReLU非线性激活函数得到另一个隐藏层输出。最后，我们将最后一个隐藏层的输出传递给self.linear3，得到输出向量y_pred。

现在让我们计算一下这个神经网络的参数数量。对于每个线性层，它都有一个权重矩阵和一个偏置向量，因此总的参数数量为：

参数数量 = d_in * h + h * h * (n-1) + h * d_out + h + d_out

其中，第一项 $d_{in} * h$ 是输入层到第一个隐藏层的权重矩阵的参数数量；第二项 $h * h * (n - 1)$ 是每个隐藏层之间的权重矩阵的参数数量；第三项 $h * d_{out}$ 是最后一个隐藏层到输出层的权重矩阵的参数数量；第四项 $h$ 和 $d_{out}$ 分别是偏置向量的参数数量。

因此，这个具有两个隐藏层的全连接神经网络的参数数量取决于输入向量的维度 $d_{in}$ ，输出向量的维度 $d_{out}$ ，每个隐藏层的神经元数量 $h$ 和隐藏层数量 $n$ 。

计算卷积神经网络的参数数量

现在让我们将上述方法扩展到卷积神经网络中。卷积神经网络是一种常用的深度学习模型，通常用于图像识别、自然语言处理等领域。它由多个卷积层、池化层、归一化层和全连接层等多种层组成。

为了计算卷积神经网络的参数数量，我们需要考虑每一层的参数数量。下面是一个简单的卷积神经网络的示例代码：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torchsummary import summary
from thop import profile

device = torch.device("cuda" if torch.cuda.is_available() else 'cpu')

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1)
        self.bn1 = nn.BatchNorm2d(16)
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, stride=1, padding=1)
        self.bn2 = nn.BatchNorm2d(32)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.fc1 = nn.Linear(32 * 8 * 8, 64)
        self.fc2 = nn.Linear(64, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = F.relu(x)
        x = self.pool1(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = F.relu(x)
        x = self.pool2(x)
        x = x.view(-1, 32 * 8 * 8)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        return x

net = Net().to(device)
input_shape = (3, 224, 224)
summary(net, input_shape)

input_tensor = torch.randn(1, *input_shape).to(device)

flops, params = profile(net, inputs=(input_tensor,))
print('FLOPs: {:.2f}M'.format(flops / 1e6))

在这个示例中，我们定义了一个包含两个卷积层、两个池化层、两个归一化层和两个全连接层的卷积神经网络。我们使用nn.Conv2d定义了两个卷积层，使用nn.BatchNorm2d定义了两个归一化层，使用nn.MaxPool2d定义了两个池化层，使用nn.Linear定义了两个全连接层。

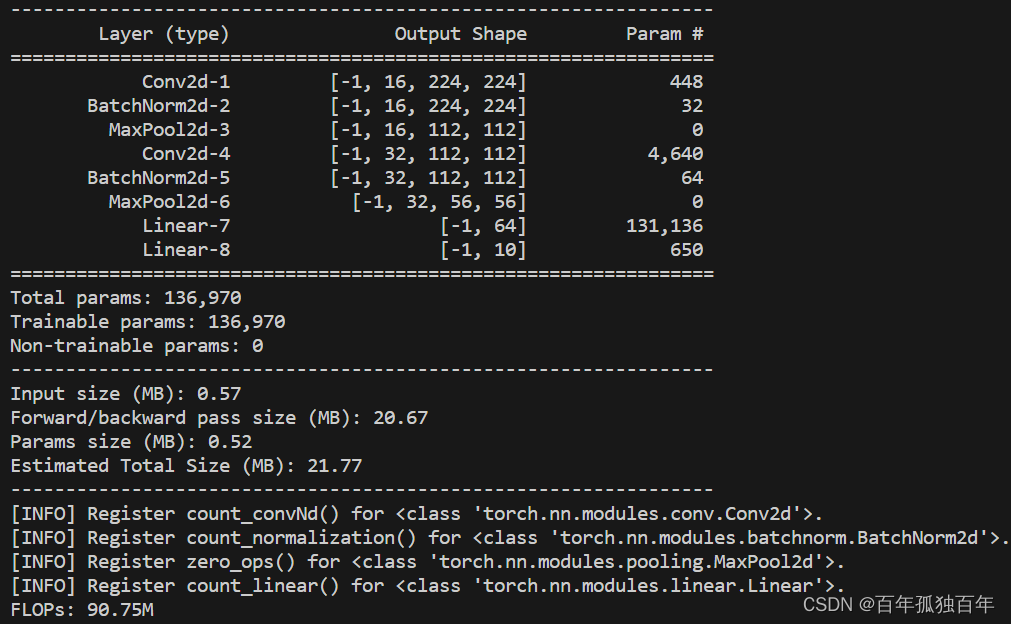
该网络结构输出如下：

在这里插入图片描述

Params计算过程

我们可以使用如下的方法计算这个卷积神经网络的参数数量：

对于每个卷积层，它有一个包含卷积核参数的权重张量和一个包含偏置参数的向量。因此，卷积层的参数数量为out_channels * (in_channels * kernel_size^2 + 1)。
对于每个归一化层，它有两个参数：缩放因子和偏移量。因此，归一化层的参数数量为2 * out_channels。
对于每个全连接层，它有一个包含权重参数的权重矩阵和一个包含偏置参数的向量。因此，全连接层的参数数量为(in_features + 1) * out_features。

根据上述公式，我们可以计算这个示例卷积神经网络的参数数量：

参数数量 = conv1参数数量 + bn1参数数量 + conv2参数数量 + bn2参数数量 + fc1参数数量 + fc2参数数量
         = 16 * (3 * 3^2 + 1) + 16 * 2 + 32 * (16 * 3^2 + 1) + 32 * 2 + (32 * 8 * 8 + 1) * 64 + (64 + 1) * 10
         = 136,970

因此，这个示例卷积神经网络的参数数量为136,970。

它计算了模型中各层的参数数量，包括卷积层、全连接层和BatchNorm层的参数数量。具体来说，公式计算了：

第一层卷积层的参数数量：输入通道数为3，输出通道数为16，卷积核大小为3x3，因此共有16个卷积核，每个卷积核有3x3=9个参数，另外还有16个偏置参数，因此该层参数数量为16x(3x3+1)=448。
第一层BatchNorm层的参数数量：该层有16个输出通道，每个通道有2个参数（缩放因子和偏置项），因此该层参数数量为16x2=32。
第二层卷积层的参数数量：输入通道数为16，输出通道数为32，卷积核大小为3x3，因此共有32个卷积核，每个卷积核有16x3x3=144个参数，另外还有32个偏置参数，因此该层参数数量为32x(16x3x3+1)=4608。
第二层BatchNorm层的参数数量：该层有32个输出通道，每个通道有2个参数，因此该层参数数量为32x2=64。
第一个全连接层的参数数量：该层输入特征数为32x8x8=2048，输出特征数为64，因此该层参数数量为2048x64+64=131,136。
第二个全连接层的参数数量：该层输入特征数为64，输出特征数为10，因此该层参数数量为64x10+10=650。

将上述各层的参数数量相加，即可得到模型的总参数数量。

另外，需要注意的是，参数数量和FLOPs是不同的概念。FLOPs是指在模型推理过程中，需要进行的浮点运算次数，而参数数量则是指模型中需要学习的参数的数量。在计算FLOPs时，需要考虑到每个卷积层、池化层和全连接层的输入输出形状，以及各层的卷积核大小、步长等参数信息。