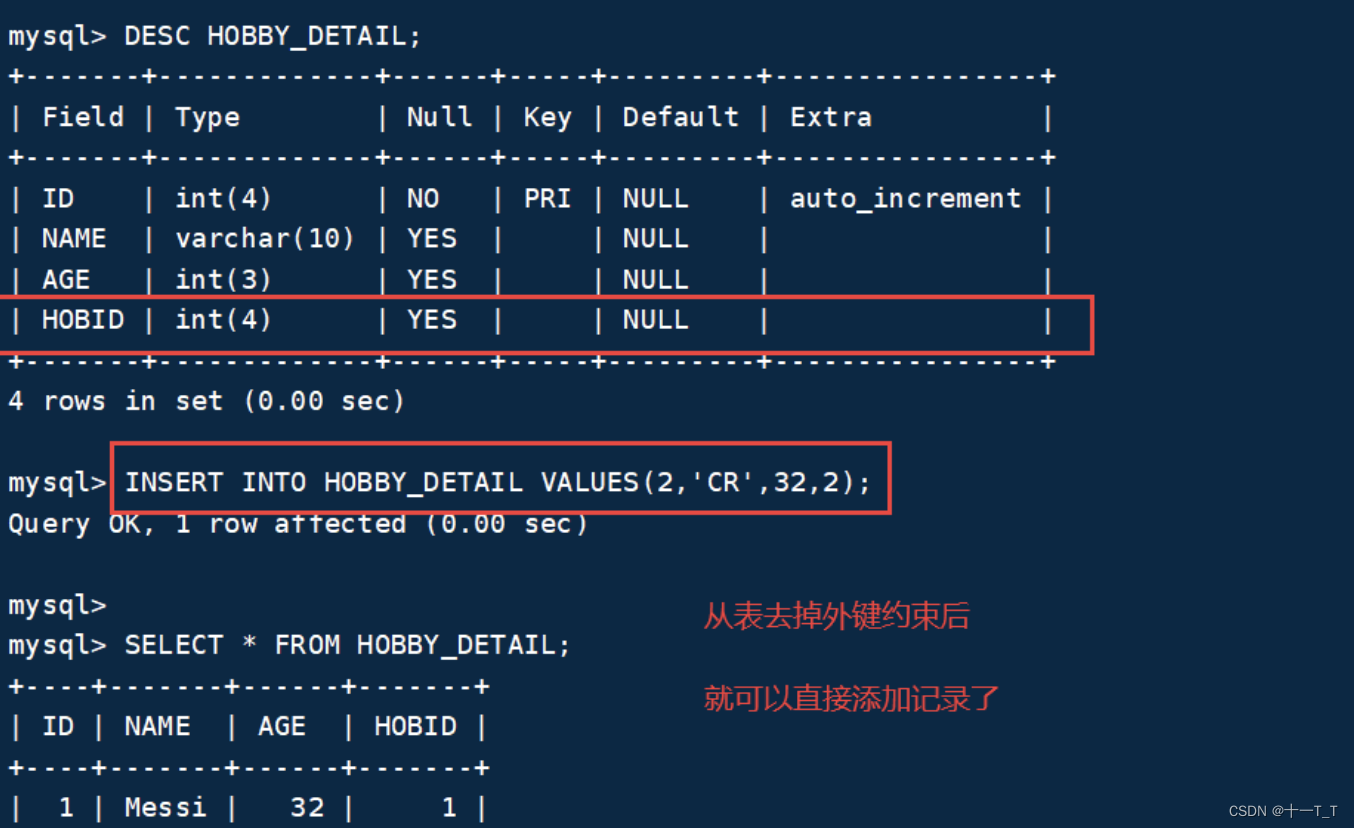
详解快速排序的优化
- 前言
- 快排的多种写法
- 霍尔法实现快排
- 代码部分
- 挖坑法
- 思路讲解
- 代码部分
- 双指针法
- 思路讲解
- 代码部分
- 针对排序数类型的优化
- 针对接近或已经有序数列和逆序数列
- 三数取中
- 代码实现
- 随机数
- 针对数字中重复度较高的数
- 三路划分
- 思路讲解
- 代码部分
- 根据递归的特点进行优化
- 插入排序优化快排
- 代码部分
- 非递归
- 代码部分
- 解释思路
前言
在博主之前刚学C的时候,曾经写了一篇快速排序
那个时候才疏学浅(虽然现在也是)
在经过深度学习了快速排序以后才知道自己对快速排序一无所知
所以特地再出了这样一篇博客用来详解快排
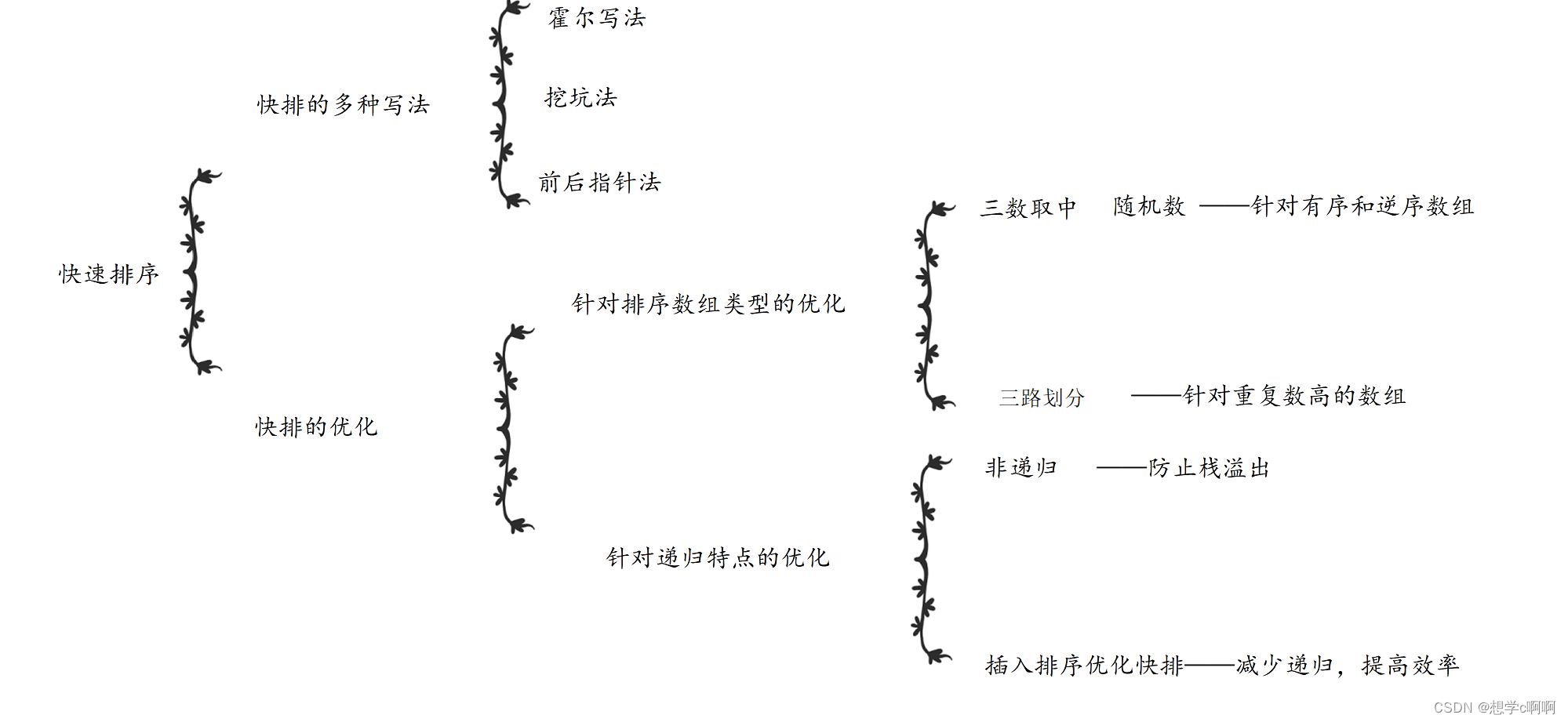
这个是本篇博客的大致内容和知识构图。
本篇也将分为多个部分来进行对树状图内容的讲解
快排的多种写法
霍尔法实现快排
这个霍尔法可以说是老朋友了,以前的老博客就是使用的霍尔法
霍尔法算是最早的快速排序,毕竟是创世人的实现法
但是有很多的坑,所以在实现时还是需要注意一下的
这里就挂个老地址:老霍尔法详解地址

这里再来张gif配合理解
代码部分
void Quick_sort(int* arr, int begin, int end)
{
if (begin >= end)
return;
int left = begin;
int right = end;
int key = begin;
while (left < right)
{
while (arr[key] <= arr[right] && left < right)
right--;
while (arr[key] >= arr[left] && left < right)
left++;
swap(arr, +
left, right);
}
swap(arr,left, key);
Quick_sort(arr, begin, left-1);
Quick_sort(arr,left+1, end);
}
挖坑法

思路讲解
这里先解释一下思路,可能看了这个动态图还不够理解。

图中默认将最左边的数字当作key值,所以直接将key值取走,此时默认原位置没有数值,所以可以看作一个坑位。
这个时候左边小人脚下有坑,此时就需要一个数字来把坑填满
这个时候右边小人就可以动起来,寻找比key值要小的数来填满(这里默认将数字升序排列)
因为坑在左边小人脚下,左边的数希望放入比key值小的数字

右边小人找到5后,接下来把拿数字把坑填过去就好。
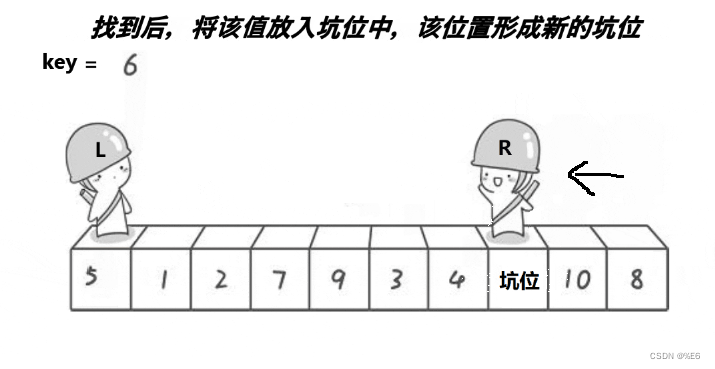
数字填过去后,右边小人脚下就有坑了,秉持着互帮互助原则,左边小人就需要找数字,帮右边的小人填好坑
右边的小人就需要比key值大的数字。
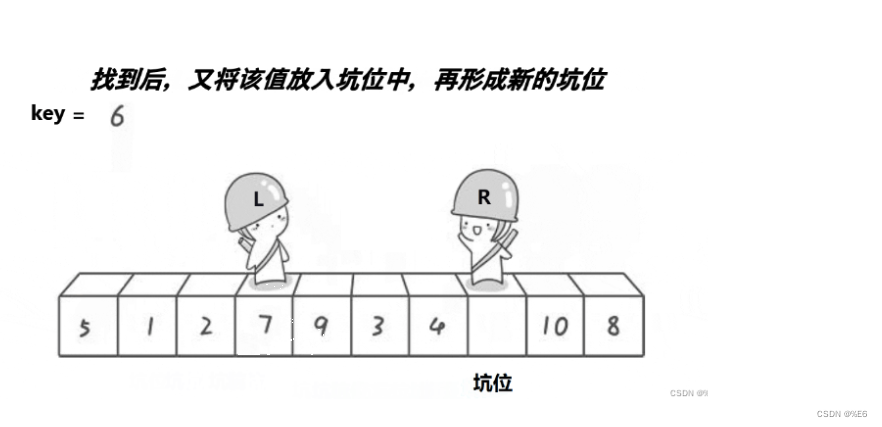
此时找到7后,就可以将R的坑填完
此时左边小人就又有坑了,就这样不停循环。

最后到坑位相遇
因为最开始是没有坑的小人先动,最后一定是不在坑上的小人向有坑的小人撞上相遇。
所以在我们拿不同的数当作key值时,取决于哪个没坑,哪个就先动
最后将key值填入相遇的坑中就可
之后就是进行递归的过程了。
代码部分
void DH_Quick_sort(int* arr,int begin,int end)
{
if (begin >= end)
return;
int left= begin;
int right=end;
int key=arr[begin];
while (left < right)
{
while (arr[right] >=key && right > left)
right--;
swap(arr, left, right);
while (arr[left] <= key && right > left)
left++;
swap(arr, left, right);
}
arr[left] = key;
DH_Quick_sort(arr, begin, left-1);
DH_Quick_sort(arr, left+1, end);
}
双指针法

这个快排的实现法算是三种写法中最简洁的。
但是同时也是比较抽象的,因为完全不同于前两种的实现思路。
思路讲解
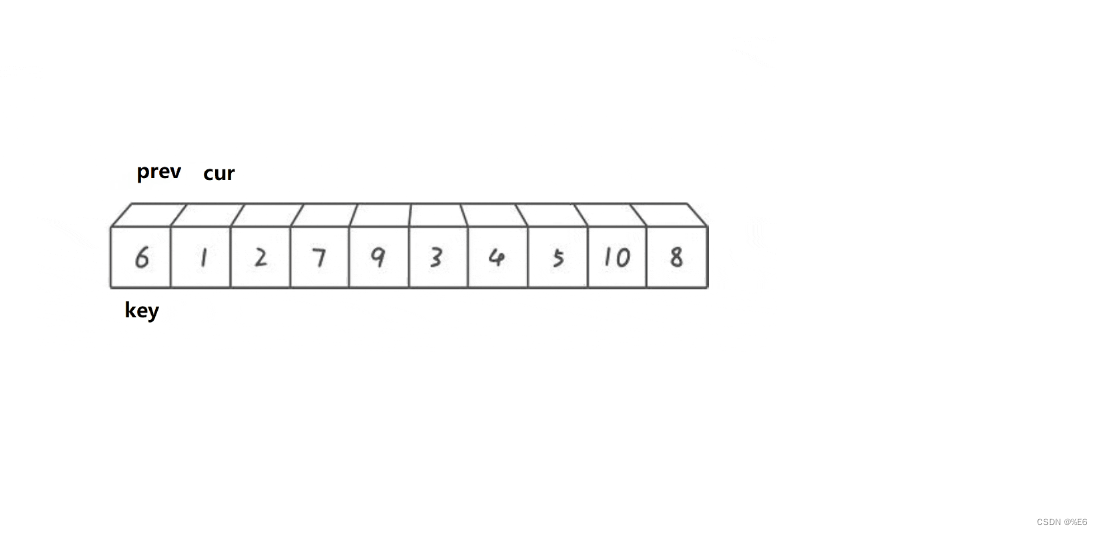
首先设定两个坐标
一个在前,用来寻找比key值小的数(因为以升序为准)
一个在后,用来进行和前坐标的交换
之后前坐标不断向前走,寻找比key值小的数字。
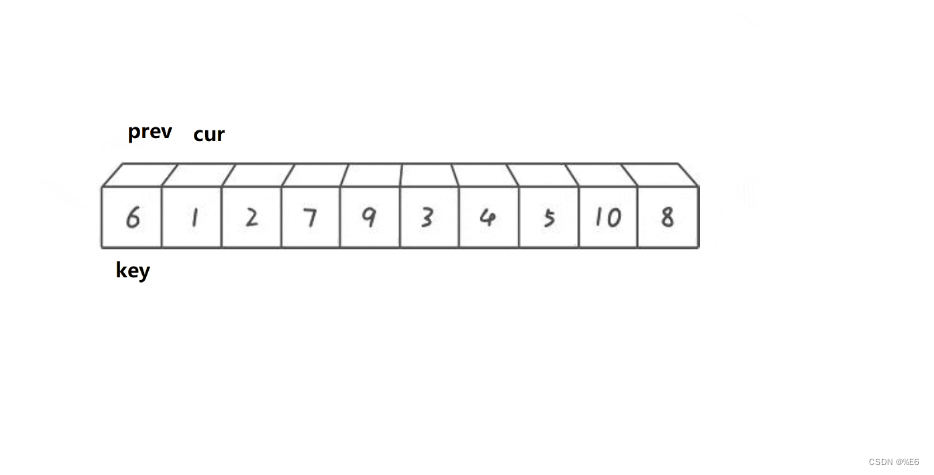
但是我们发现,一开始的状态就是cur在小于key值的数字上。
那这样能交换吗?
显然是不可以的,因为我们此时prev是在key值上面
key一开始是不能被交换的
所以我们需要一开始就对prev进行++
这里直接把部分实现代码放出来比较好理解
if (arr[cur] <= arr[key] && ++prev != cur)
swap(arr, prev, cur);
这里我们就能看到当cur所在的值比key值小时,会进行判断,对prev进行++,++后判断prev是否与cur相等。
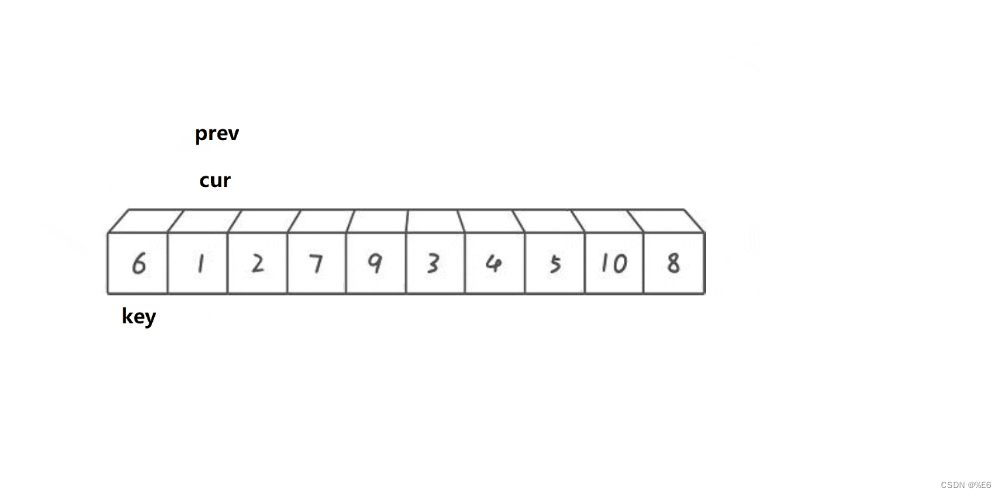
对prev++后这样显然不能进行交换,所以cur还是需要继续往前走。
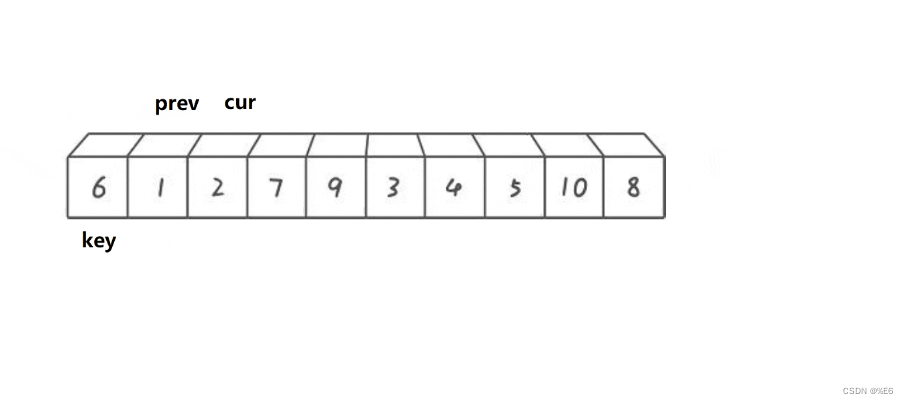
cur走到2处时
if (arr[cur] <= arr[key] && ++prev != cur)
前部分生效,进行对prev的++

发现prev++后与cur相等,所以cur继续前进。
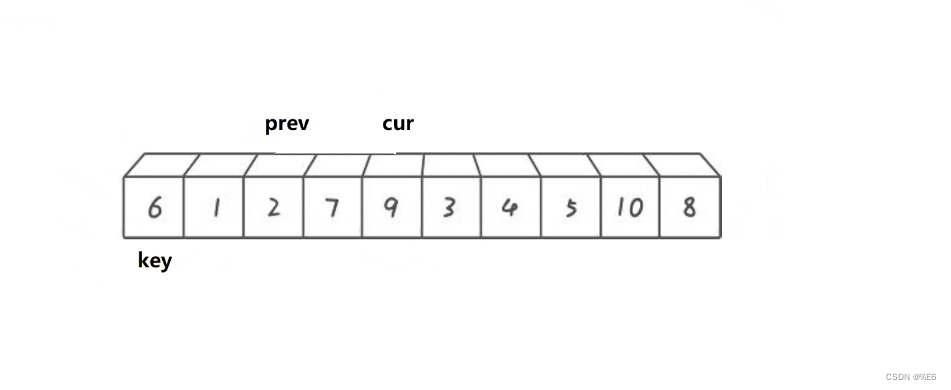
cur碰到7后继续++
判断前半部分没生效,所以后半prev++不会触发
所以cur继续++,加到9
同样判断前半部分没生效,所以后半prev++不会触发。
所以prev停留在2处
cur到了3时
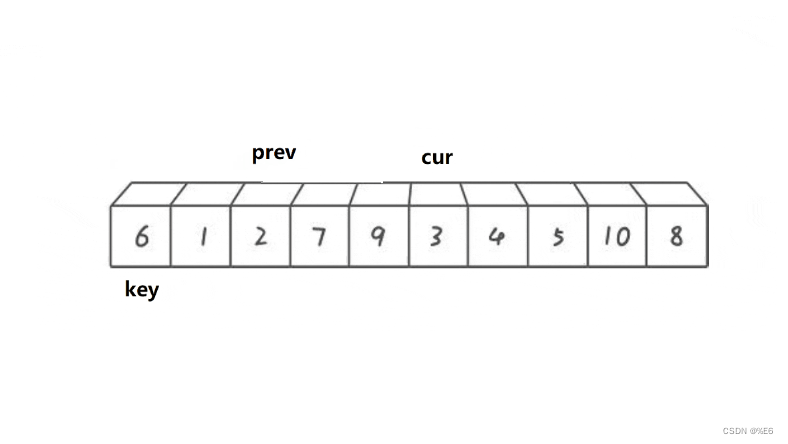
判断部分前后全都触发,prev++
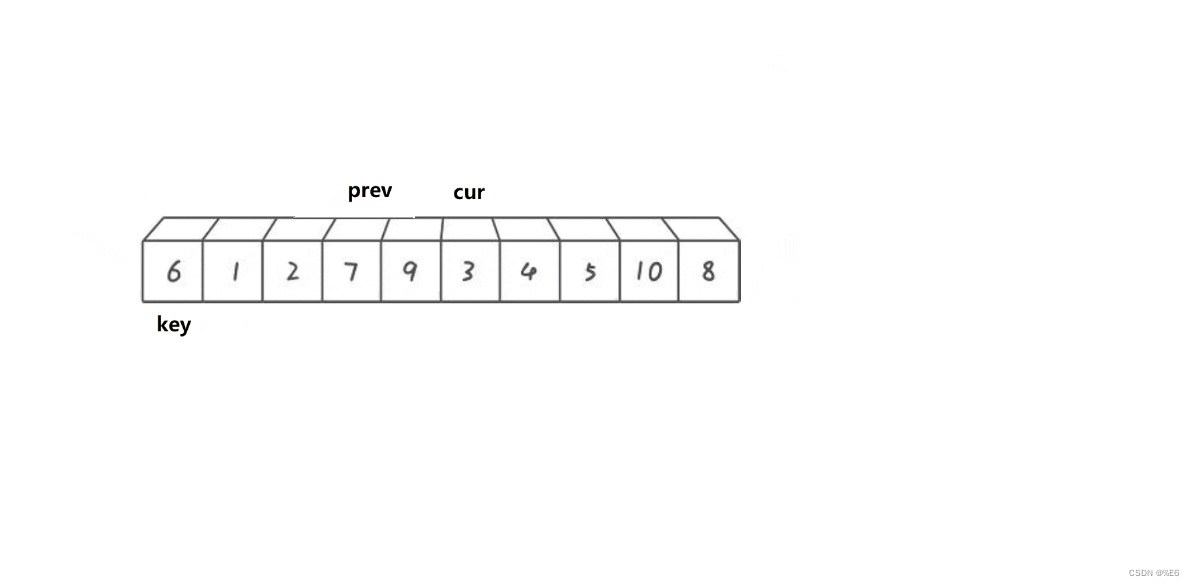
发现prev与cur并不相同,此时就进行交换
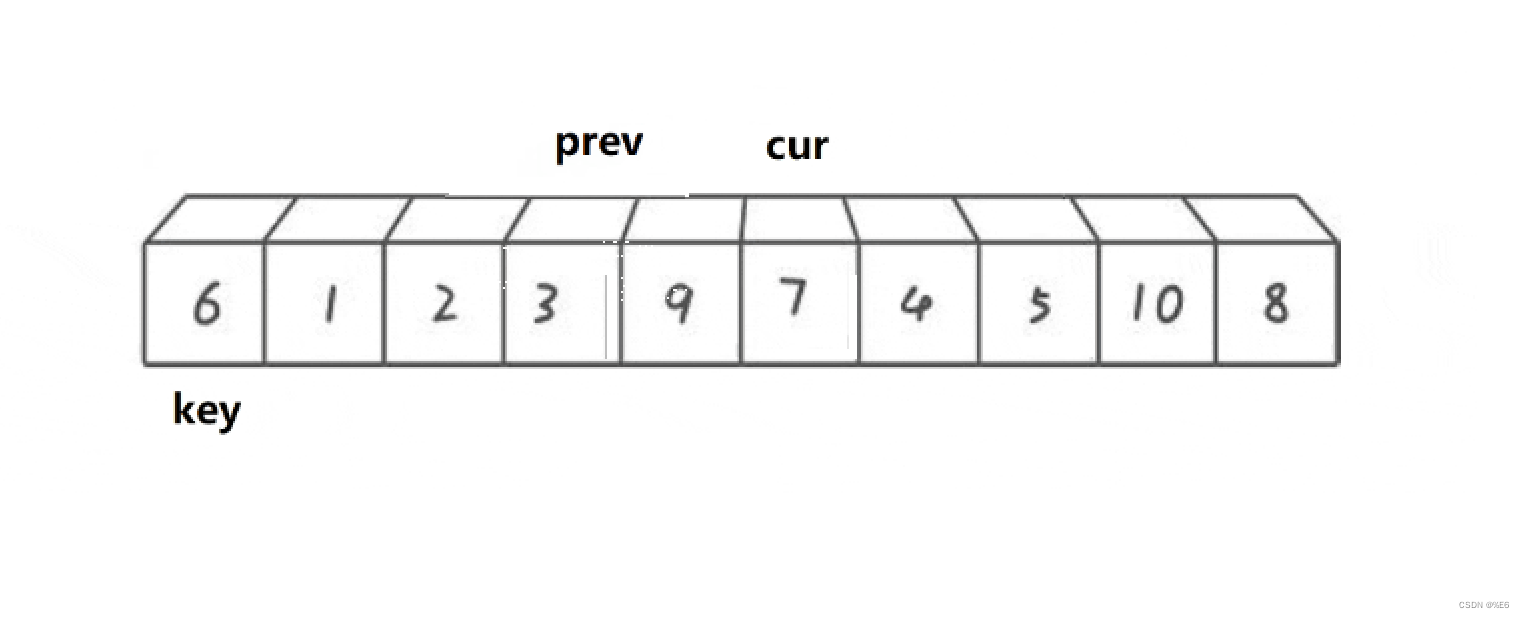
之后cur继续前进
那为什么要这样设置prev的++判断呢?
**这样可以防止prev和cur相邻的情况
使cur碰到大于key值的节点后才能和prev拉开距离
**
这样就可以防止使两个相邻的小于key值的数进行无效
交换
保证了cur交换的值必定是大于key值的数和小于key值的数进行交换
同时,一开始prev是在key上,所以先++可以防止key值被交换走
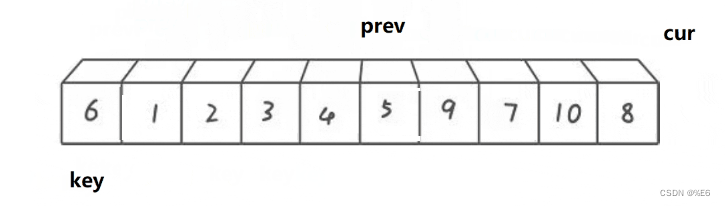
此时就可以cur越界,key与prev进行交换,最后执行递归即可
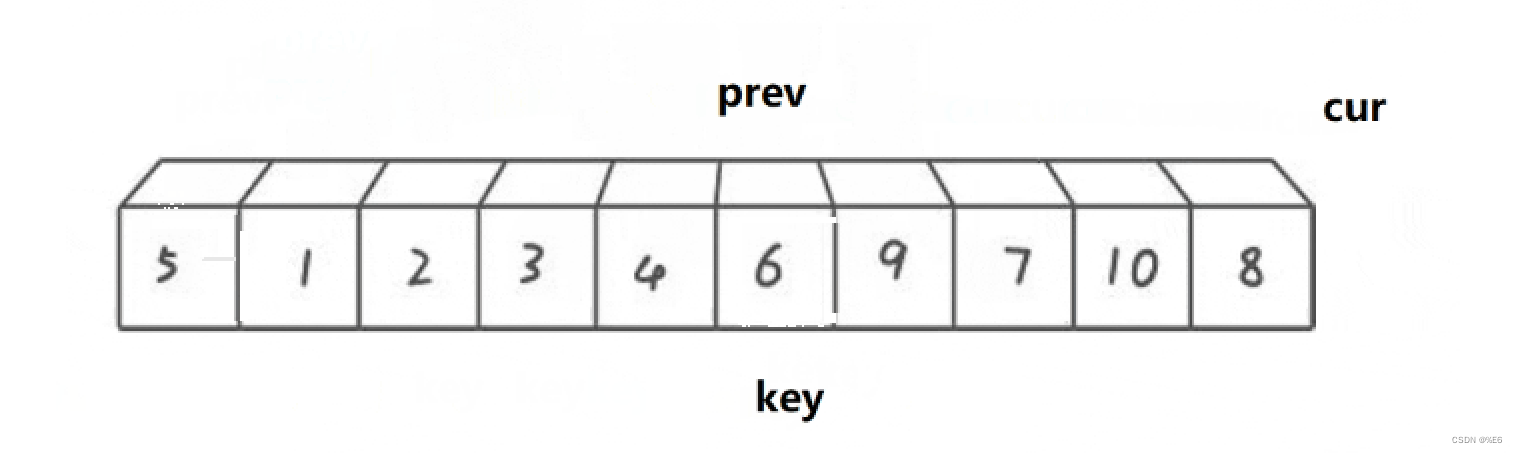
代码部分
void DPt_Quick_sort(int* arr, int begin, int end)
{
if (begin >= end)
return;
//这里不能用指针,不好进行赋值和传参
//所以在前面讲解时用的是坐标一词
int prev = begin;
int cur = begin+1;
int key = begin;
while (cur <= end)
{
if (arr[cur] <= arr[key] && ++prev != cur)
swap(arr, prev, cur);
cur++;
}
swap(arr, prev, key);
DPt_Quick_sort(arr, begin, prev-1);
DPt_Quick_sort(arr, prev+1, end);
}
针对排序数类型的优化
针对接近或已经有序数列和逆序数列
众所周知,当我们使用快排时,默认将数组中的最左边的数当作比较值时

当对这样一个有序数组进行排序时
假设我们使用的是霍尔法

right会直接跑到left处。
此时进行递归命令时
Quick_sort(arr, begin, left-1);
Quick_sort(arr,left+1, end);
此时数组就会被分成
这样差距极大的两组进行递归。
众所周知递归最快的,深度最小的方式时
对一个数组进行(n/2)的分开递归
这样将一个数组分成两个差距极大的数组进行排列是十分麻烦的。
所以就出现了优化方法
三数取中
这个方法原理就是
在进行取key值时,不使用默认的最左端的值当作key
将最左端和最右端的数以及他们中间的数进行比较
取出一个中间值当作key值
代码实现
int GetNumMid(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[left] > arr[right])
{
if (arr[left] < arr[mid])
return left;
if (arr[left] > arr[mid] && arr[mid] < arr[right])
return right;
if (arr[left] > arr[mid] && arr[mid] > arr[right])
return mid;
if (arr[left] == arr[mid] || arr[right] == arr[mid])
return mid;
}
else if (arr[left] < arr[right])
{
if (arr[left] > arr[mid])
return left;
if (arr[mid] > arr[right])
return right;
if (arr[mid] > arr[left] && arr[mid] < arr[right])
return mid;
if (arr[mid] > arr[left] && arr[mid] > arr[right])
return right;
if (arr[right] == arr[mid] || arr[left] == arr[mid])
return mid;
}
else
return right;
}
void Quick_sort_GM(int* arr, int begin, int end)
{
if (begin >= end)
return;
int left=begin;
int right=end;
//取出中间值
int mid=GetNumMid(arr, left, right);
//将中间值和最左端的值交换
//就是将新key移动到最左端
if (mid != left)
swap(arr, mid, left);
int key = left;
while (left < right)
{
while (arr[right] >= arr[key] && left < right)
right--;
while (arr[left] <= arr[key] && left < right)
left++;
swap(arr, left, right);
}
swap(arr, left, key);
Quick_sort_GM(arr, begin, left - 1);
Quick_sort_GM(arr, left+1, end);
}

这样以后将key作为三数中的中间大的数作为值,有效防止了之前的情况。
随机数
随机数就是将key值用数组中随机一个数,作为key值进行比较交换。
这个其实比较吃运气,这个代码就略了,个人认为三数取中更为巧妙一点,而且代码不难,就是随机生成一个数。
针对数字中重复度较高的数
与有序和逆序数列同理,如果一个数组一个相同的数字占多,就会让左右节点相遇较晚,使递归的两个数列分的数差距较大,增加递归的深度,降低效率
三路划分
思路讲解
我们原本实现快速排序,通过的时候两路划分

这样会省去等于key值的数,所以会导致遇到相同的数字时,递归的数字分配的不好。
所以就产生了我们的三路划分优化

就是说将小于等于key值的数放到中间,这里随便举一个例子谈谈过程。
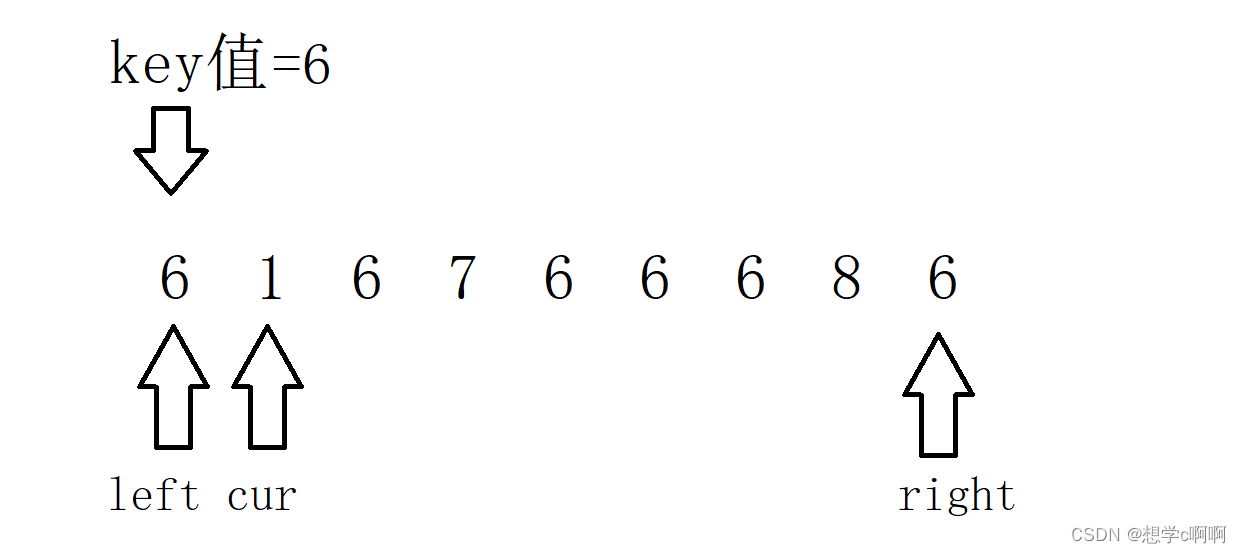
三路划分需要设定三个指针,这里我们就边走边看情况
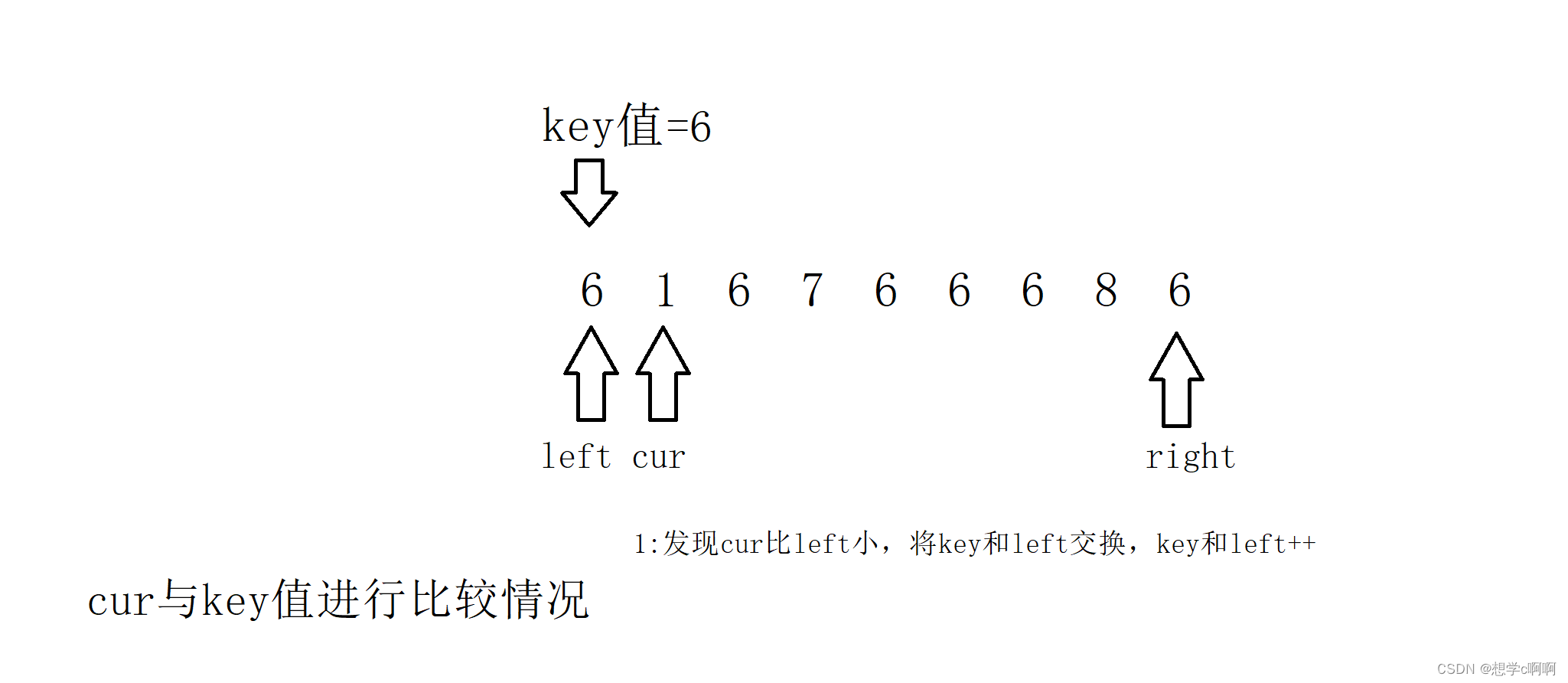
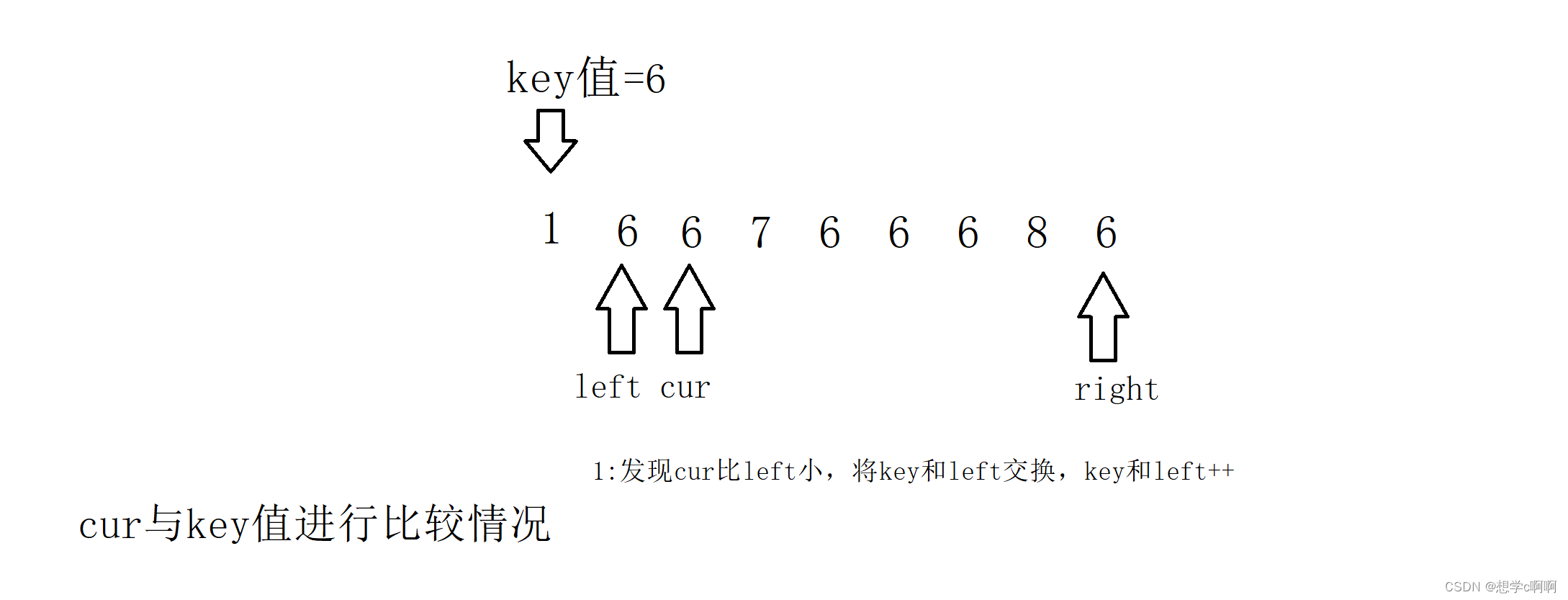
这样就走好了一步,cur继续比较,(这个key知识用来存储key值的,原本的位置换走了也没什么关系,(忘记把箭头去掉了))
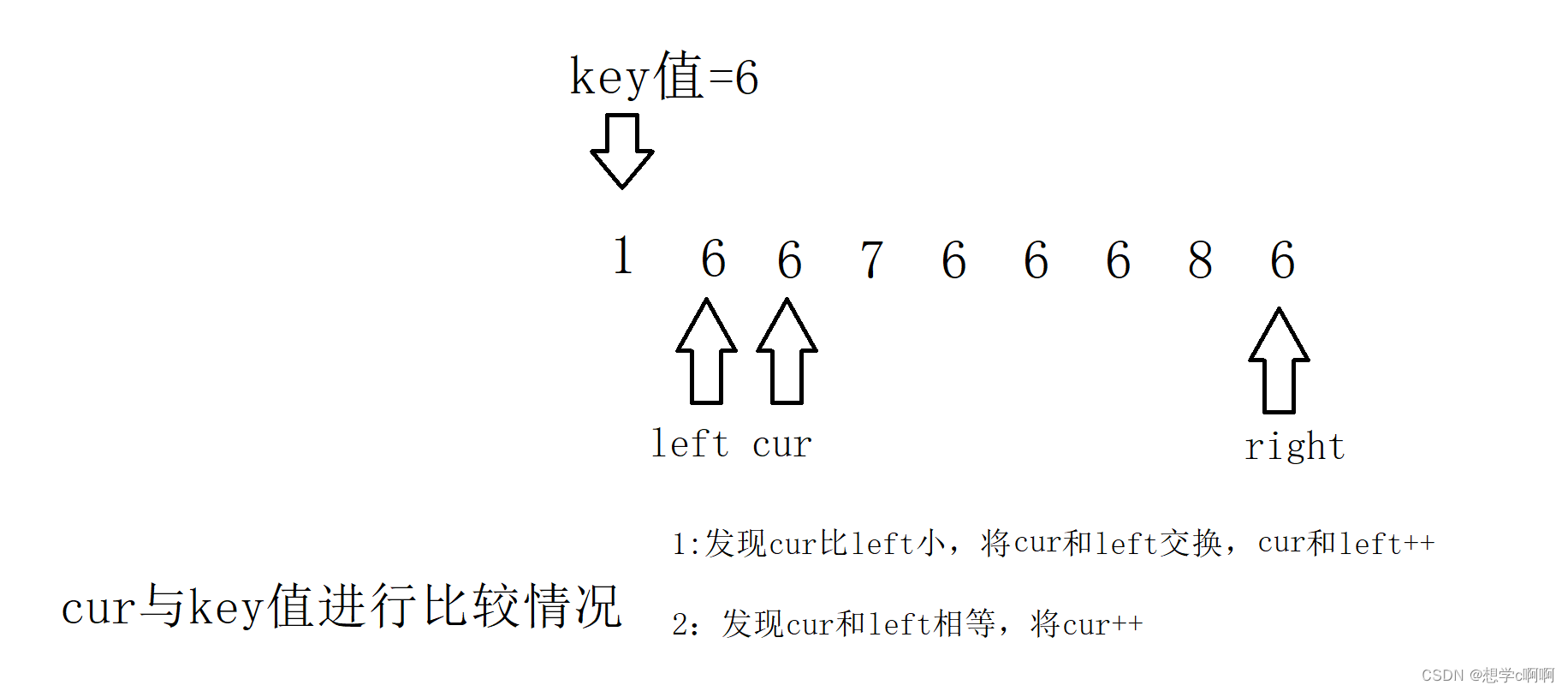
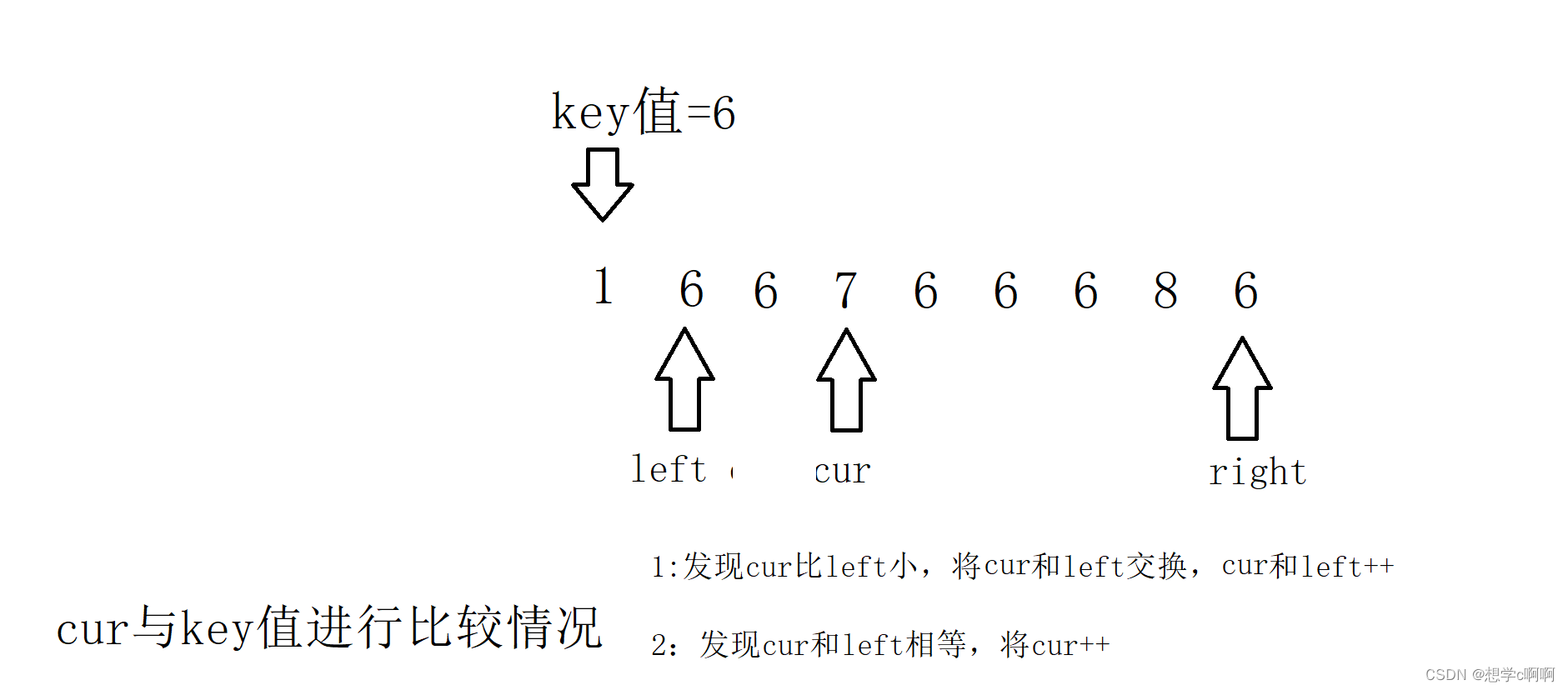
cur这时又发现了情况的不一样
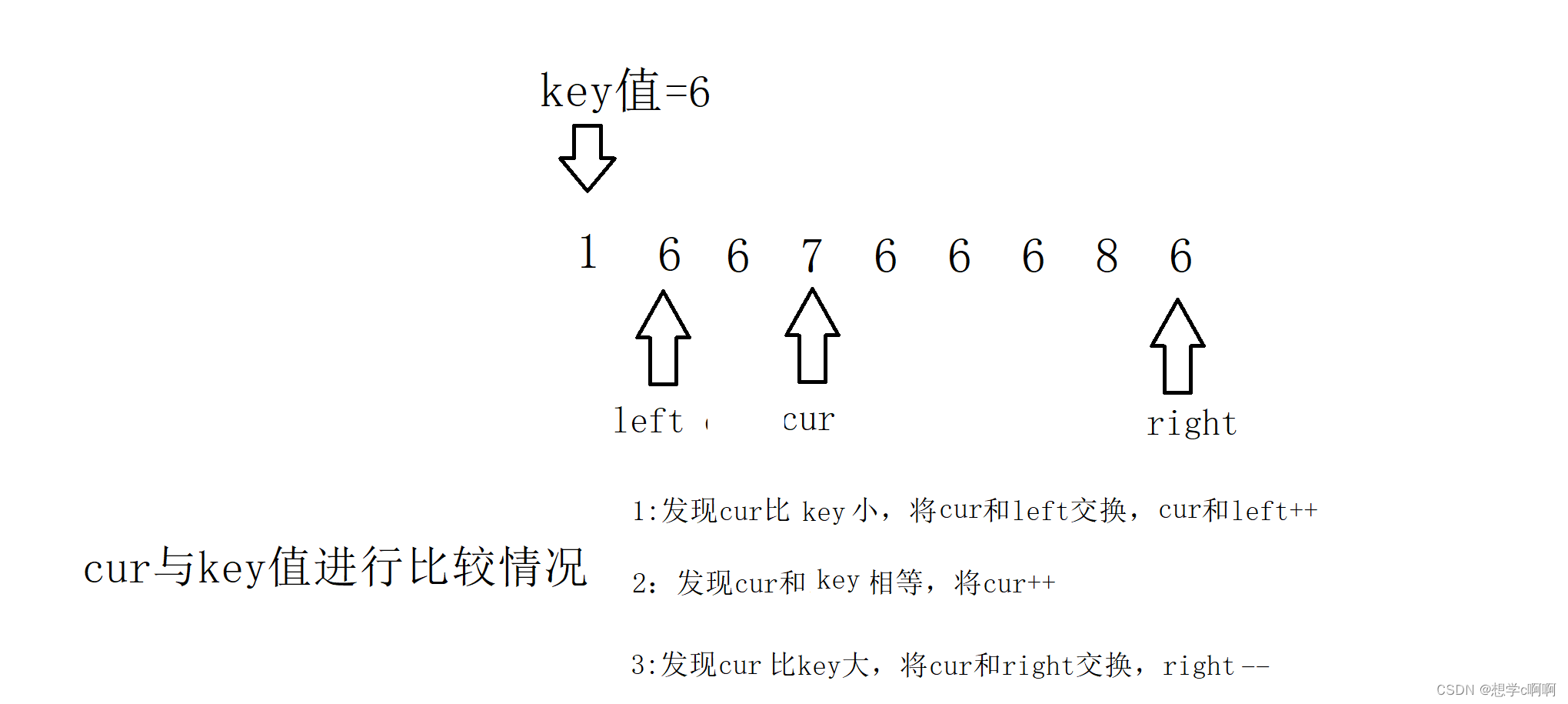
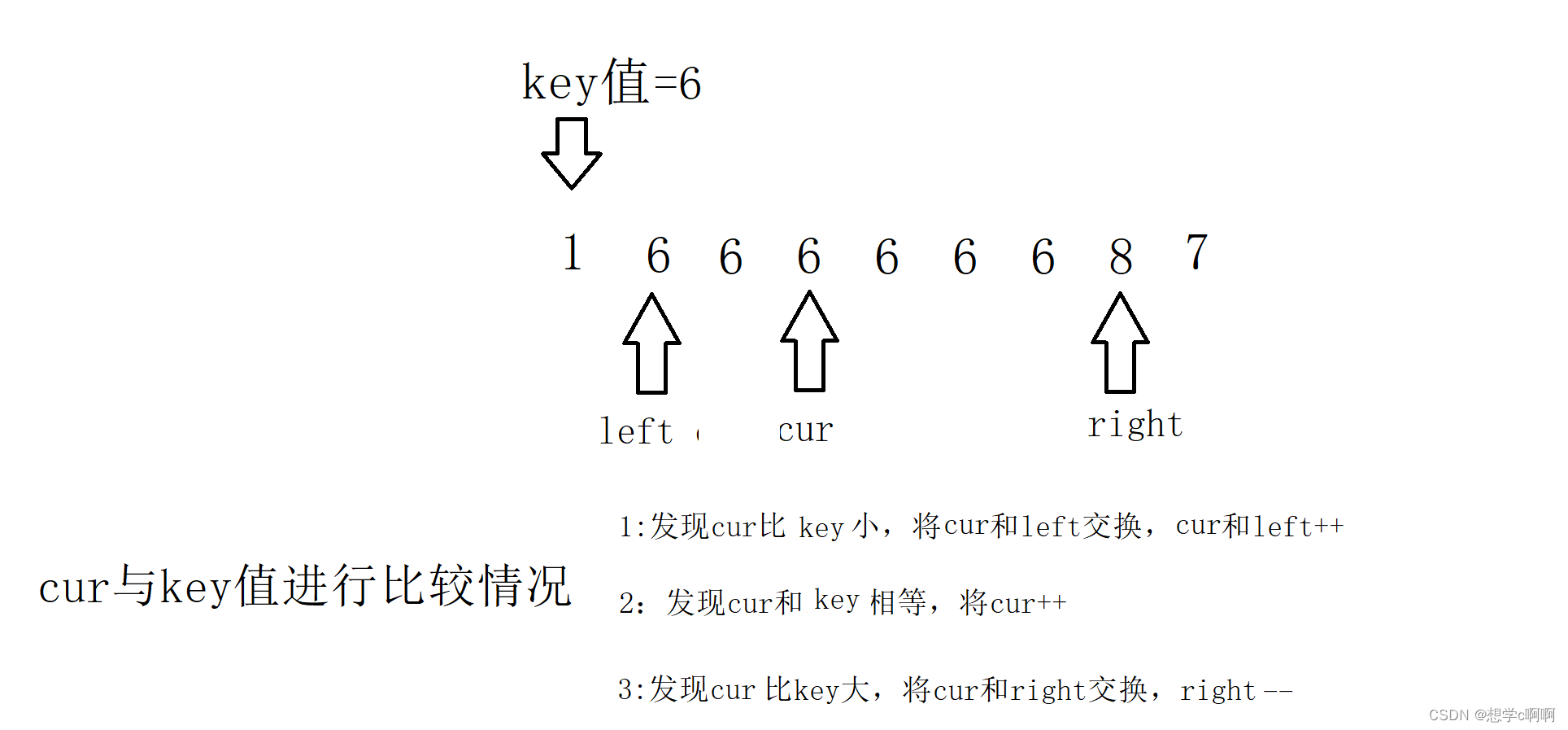
这样三种情况都好了,接下来结束条件就是cur和right相遇的一刻
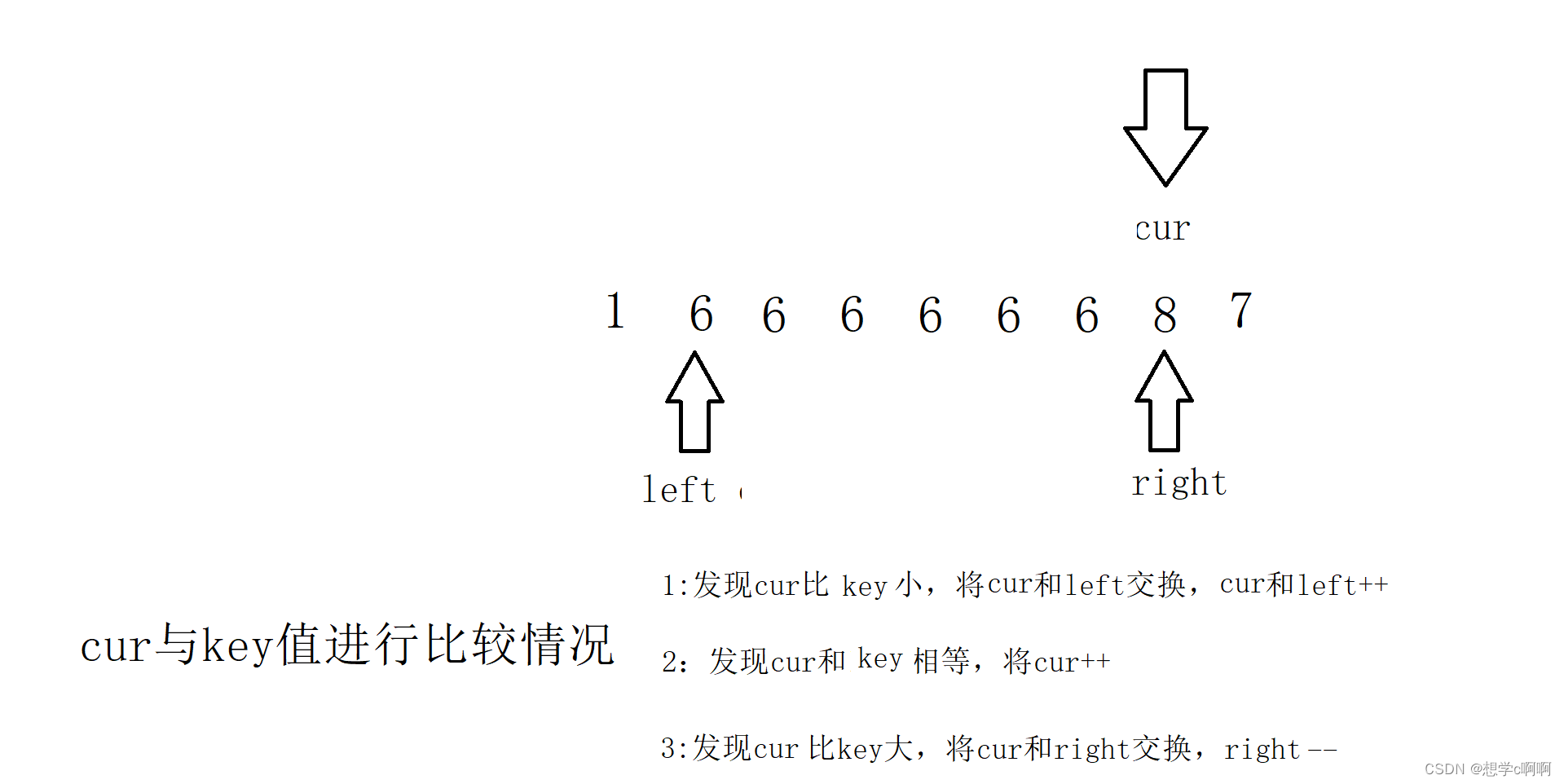

这样递归数列就被成了这样三个部分,中间部分可以不用进行递归,只需要把左边和右边的区间进行递归就可以了
代码部分
void Twd_Quick_sort(int* arr,int begin,int end)
{
if (begin >= end)
return;
int left = begin;
int key = arr[begin];
int right = end;
int cur = left + 1;
while ( cur <= right)
{
if (key < arr[cur])
{
swap(arr, cur, right);
right--;
}
else if (key > arr[cur])
{
swap(arr,cur,left);
cur++;
left++;
}
else
{
cur++;
}
}
Twd_Quick_sort(arr, begin, left - 1);
Twd_Quick_sort(arr, right + 1, end);
}
根据递归的特点进行优化
插入排序优化快排
众所周知,插入排序的特点是,越接近有序的数组,插入排序的效率就越高。
希尔排序就是依据插入排序这个特点而优化产生的。
那我们是不是也可以用插入排序来优化快速排序呢?
答案确实是可以的
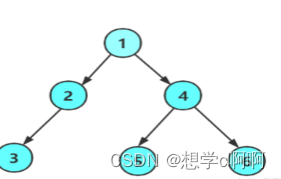
我们知道递归算法如果分割合理,就是一颗完美二叉树,这里我们就用二叉树做例子。
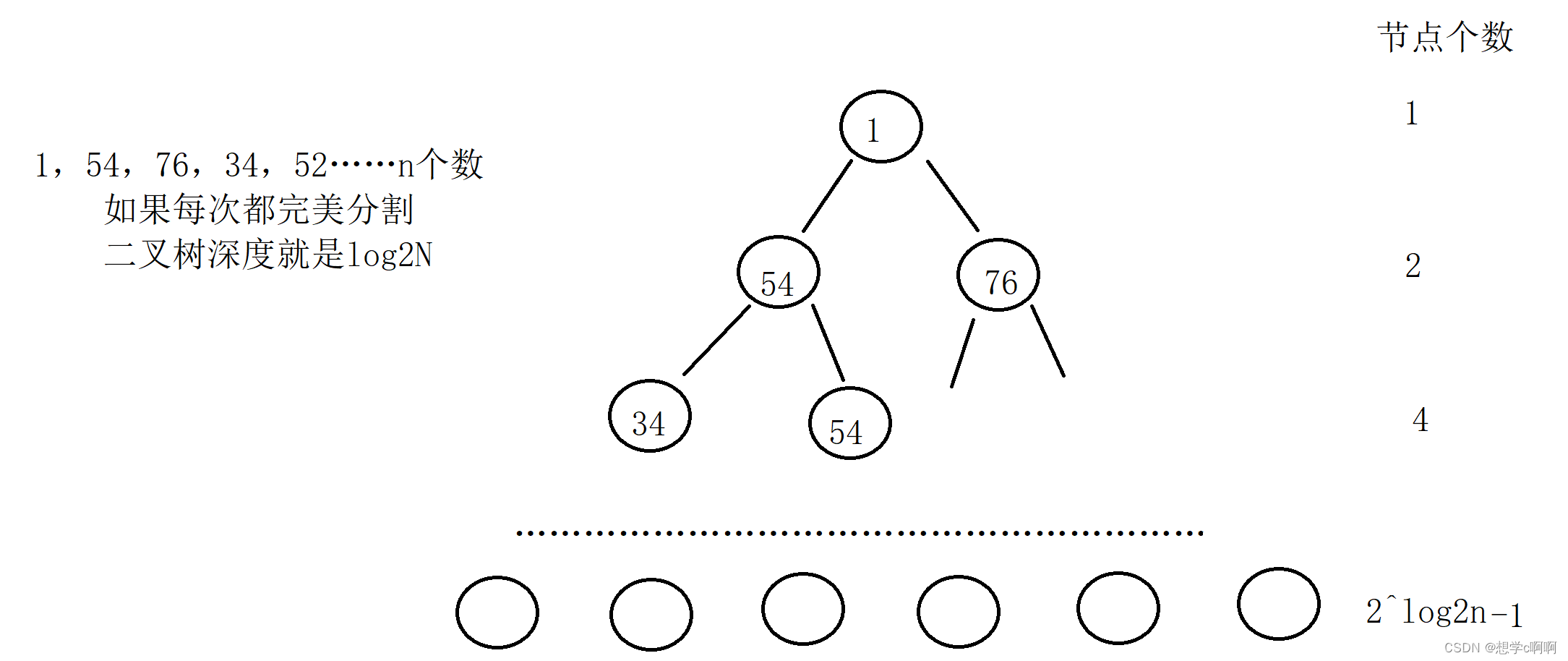
从图上可以看到最后一层的递归节点个数占了递归的绝大部分,并且这个时候数组也接近有序,正好可以用插入排序进行优化。
代码部分
void insert_Quick_sort(int* arr, int begin, int end)
{
if (begin >= end)
return;
if ((end - begin + 1) < 3)
{
int left = begin;
int right = end;
int key = begin;
while (left < right)
{
while (arr[key] <= arr[right] && left < right)
right--;
while (arr[key] >= arr[left] && left < right)
left++;
swap(arr, left, right);
}
swap(arr, left, key);
insert_Quick_sort(arr, begin, left - 1);
insert_Quick_sort(arr, left + 1, end);
}
else
insert_sort_left(arr+begin,end-begin+1);
}
这里主要就是控制right和left之间的数字间隔,来进行选择是进行递归还是进行插入排序。
非递归
递归最大的缺点是什么?就是容易导致栈溢出。
这个应该人人都知道,递归需要不停对栈帧申请空间,然后就会导致栈溢出,而这个时候就需要改成非递归。
基本上能用递归写的都需要学会转化成非递归。
我们要模仿递归时,首先要了解递归每次在干什么。
递归每次传值时
insert_Quick_sort(arr, begin, left - 1);
insert_Quick_sort(arr, left + 1, end);
这个递归每次在跑时,都是传了下一次要排序的区间。
了解了这个以后,我们想要模拟实现递归,就需要把每次需要排序的区间给记录下来
区间就是数据,而处理数据的结构,就是我们在学的数据结构,在我们以前学的结构中,有啥结构可以完美处理呢?没错,就是栈,其实队列也可以
但是能用顺序表的地方尽量用顺序表,而不是链表。
代码部分
int part_sort(int* arr, int begin, int end)
{
int left = begin;
int right = end;
int key = begin;
while (left < right)
{
while (arr[key] <= arr[right] && left < right)
right--;
while (arr[key] >= arr[left] && left < right)
left++;
swap(arr, left, right);
}
swap(arr, left, key);
return key;
}
void Quick_Sort_UNrecursion(int* arr,int left,int right)
{
Stack ST;
STinit(&ST);
STpush(&ST, right);
STpush(&ST, left);
while (!STempty(&ST))
{
int begin = STtop(&ST);
STpop(&ST);
int end = STtop(&ST);
STpop(&ST);
int keyi=part_sort(arr, begin, end);
if(end>keyi+1)
{
STpush(&ST, end);
STpush(&ST, keyi + 1);
}
if (begin < keyi - 1)
{
STpush(&ST, keyi - 1);
STpush(&ST, begin);
}
}
STdestroy(&ST);
}
解释思路
这里我们选择先看代码进行解释,便于理解
int part_sort(int* arr, int begin, int end)
{
int left = begin;
int right = end;
int key = begin;
while (left < right)
{
while (arr[key] <= arr[right] && left < right)
right--;
while (arr[key] >= arr[left] && left < right)
left++;
swap(arr, left, right);
}
swap(arr, left, key);
return key;
}
这个部分是将霍尔快排的单个排序取了出来。
我们主要看实现递归的部分
Stack ST;
STinit(&ST);
STpush(&ST, right);
STpush(&ST, left);
这里我们首先初始化栈,然后先将最开始的begin和end排序区间存入
这里我们先将right放入,之后再访问时要先读取left(因为栈)
while (!STempty(&ST))
{
int begin = STtop(&ST);
STpop(&ST);
int end = STtop(&ST);
STpop(&ST);
int keyi=part_sort(arr, begin, end);
这里的top 和pop是对左区间和右区间进行读取,并进行出栈
最后将区间内的数进行排列,并将下两个排序的区间割点存储。
//这里的范围是begin key-1 【key】 key+1 end
if(end>keyi+1)
{
STpush(&ST, end);
STpush(&ST, keyi + 1);
}
if (begin < keyi - 1)
{
STpush(&ST, keyi - 1);
STpush(&ST, begin);
}
}
STdestroy(&ST);
判断当节点范围
如果只有一个数或不存在时则退出
否则 存入。
所以循环的结束点以 while (!STempty(&ST))栈为空则停止
当栈中的待排序区间全都排序结束时则排序完成



![K8S管理系统项目实战[前端开发]-1](https://img-blog.csdnimg.cn/4c1121bf152d4b7285376480f4e2a850.png)