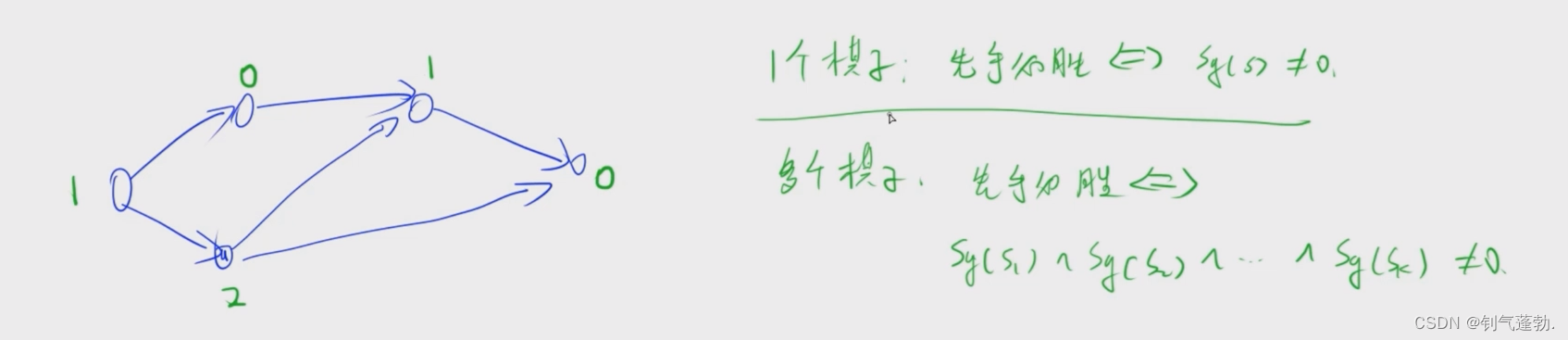
1.移棋子游戏

mex为最小的不存在的自然数
#include<bits/stdc++.h>
using namespace std;
const int N=2e3+10,M=2e4+10;
int h[N],e[M],ne[M],idx;
int n,m,k;
int f[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int sg(int u)//求sg函数
{
if(f[u]!=-1) return f[u];
set<int> S;//存集合中的已经有的自然数
for(int i=h[u];~i;i=ne[i])//枚举所有能到的边
{
int j=e[i];
S.insert(sg(j));//把能到的点的sg值放进集合中
}
for(int i=0;;i++)//枚举集合中不存在的最小自然数
if(S.count(i)==0) return f[u]=i;//返回即可
}
int main()
{
memset(h,-1,sizeof h);
memset(f,-1,sizeof f);//初始化为-1表示没有给过值
scanf("%d%d%d",&n,&m,&k);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
}
int res=0;//一开始是0,你也可以给1或者其他输,但是判断时对应要改
while(k--)
{
int u;
scanf("%d",&u);
res^=sg(u);//异或每个棋子的sg值
}
if(res==0) puts("lose");//假如异或后是一开始的res则就输
else puts("win");
return 0;
}
2.取石子
结论:在所有堆的石子个数>1的情况下
只要石子数+石子的堆d数-1==b是奇数,那么先手必胜。b是不计算所有个数为1的石子堆得出的。的
b是奇数的情况下一定存在一个偶数后继,是偶数的情况下一定是奇数后继
证明
a是石子为1的堆,b是 石子大于1的堆+堆里是石子总数-1

第四个合并a中两个,说明出现的一堆大于1的堆然后b就+1(合并出来的堆)+2(多的两个石子)
为什么b==0和不等于0的情况影响不一样 因为第一次要先减一个1 后面都不需要
b是 石子大于1的堆+堆里是石子总数-1
#include<bits/stdc++.h>
using namespace std;
const int N=55,M=50010;
int f[N][M];
int dp(int a,int b)
{
int &v=f[a][b];
if(v!=-1) return v;//假如求过
if(!a) return v=b%2;//假如个数为1的堆是空,则直接返回b是不是奇数
if(b==1) return dp(a+1,0);//假如b是1了,说明b中最后一堆只有一个数放在a中
if(a&&!dp(a-1,b)) return v=1;//a中取一个
if(b&&!dp(a,b-1)) return v=1;//b中取一个或者合并b中两堆
if(a>=2&&!dp(a-2,b+(b?3:2))) return v=1;//合并一个数的堆,则变成了一个个数为2的堆,加到b中
if(a&&b&&!dp(a-1,b+1)) return v=1;//合并a b中个一堆
return v=0;
}
int main()
{
memset(f,-1,sizeof f);//初始化为-1,表示没用过
int T;
scanf("%d",&T);
while(T--)
{
//不用重新初始化因为每次的状态是一样的
int n;
scanf("%d",&n);
int a=0,b=0;
for(int i=0;i<n;i++)
{
int x;
scanf("%d",&x);
if(x==1) a++;//假如个数是1个,则一个数的堆++
else b+=b?x+1:x;//假如b是0,则加1个,反之加x+1个
}
if(dp(a,b)) puts("YES");//看看能不能走到必胜态
else puts("NO");
}
return 0;
}
3.取石子游戏
待细补
n堆石子只能取左右堆的石子,可以取任意个>0&&<=堆的总数,没得操作的输
定义一个left[i][j]跟right[i][j],表示在i,j这个状态的左边放多少个棋子可以使先手必败,right也同理
答案就是判断一下left[[2][n]==a[1],假如等于就是先手必败,反之必胜
left[i][j]的推法:

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
int a[N];
int l[N][N],r[N][N];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int len=1;len<=n;len++)//枚举区间长度
for(int i=1;i+len-1<=n;i++)//枚举左右l,r
{
int j=i+len-1;//左边的j
if(len==1) l[i][j]=r[i][j]=a[i];//假如长度是1,则左右边直接给相同的石子即可
else
{
//先求left[i][j]
int L=l[i][j-1],R=r[i][j-1],X=a[j];
if(R==X) l[i][j]=0;//判断1
else if(X<L&&X<R||X>L&&X>R) l[i][j]=X;//判断2和5
else if(L>R) l[i][j]=X-1;//判断3
else l[i][j]=X+1;//判断4
//在求right[i][j]做法一样
L=l[i+1][j],R=r[i+1][j],X=a[i];
if(L==X) r[i][j]=0;
else if(X<L&&X<R||X>L&&X>R) r[i][j]=X;
else if(R>L) r[i][j]=X-1;
else r[i][j]=X+1;
}
}
if(n==1) puts("1");
else printf("%d\n",l[2][n]!=a[1]);//判断先手是否不是必败即可
}
return 0;
}