本篇博客会讲解力扣“69. x 的平方根”这道题的解题思路。这是题目链接。

大家先来审下题：

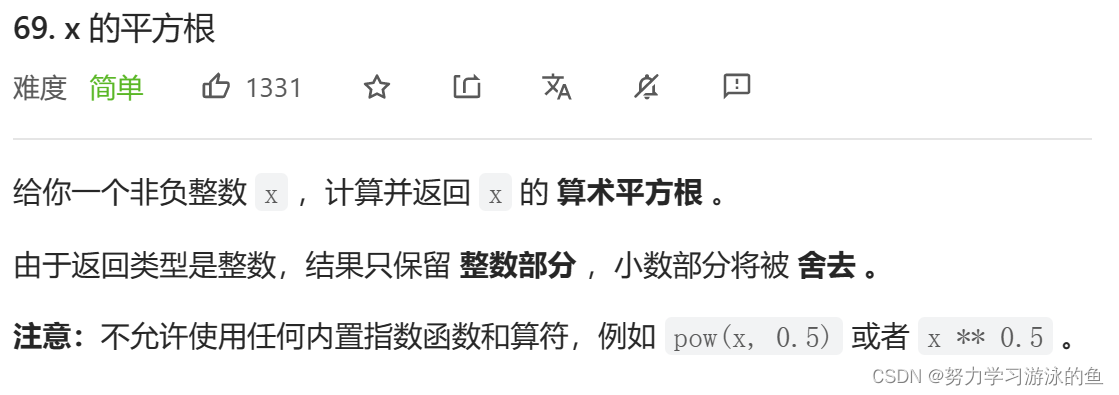
以及示例：

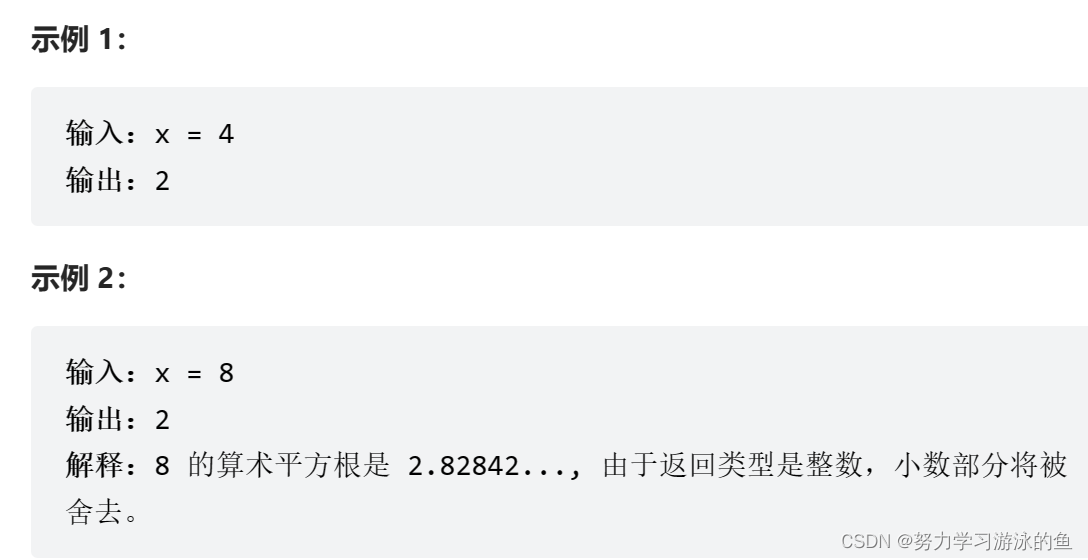
还有提示：

本题常规的思路有：暴力查找、转换成指数和对数、二分查找、牛顿迭代。

转换成指数和对数的方法非常简单：x^0.5=ln(exp(x^0.5))=ln(0.5exp(x))，直接调用对应的库函数求解即可。牛顿迭代是我在“数值方法”这门专业课学到的方法（博主是学数学的），讲解起来可能有点复杂，这里就不讲解了。

我还是更加推荐查找的思路。暴力查找过于直接，效率太低，所以采取的是优化的方案：二分查找。二分查找思路简单，没有牛顿迭代这种非常复杂的数学推导，同时不用调用数学库函数，效率也还行，为O(logN)。

首先需要把这道题转换一下：在[0,x]中查找一个最大的数n，使得n*n<=x即可。所以直接手撕二分查找：

int mySqrt(int x){
	// [0,x]二分查找
    int left = 0;
    int right = x;
    while (left <= right)
    {
        // 求left和right的平均数
        int mid = left + (right-left) / 2;
        if (mid*mid > x)
        {

        }
        else if (mid*mid < x)
        {

        }
        else
        {
            // 找到了
            return mid;
        }
    }
}

大家很容易写出来上面的代码。接下来需要分析一下：如果mid*mid > x，说明mid已经比x的算术平方根大了，此时应该往“小的方向”找，也就是到区间左半边找，反之同理。

int mySqrt(int x){
	// [0,x]二分查找
    int left = 0;
    int right = x;
    while (left <= right)
    {
        // 求left和right的平均数
        int mid = left + (right-left) / 2;
        if (mid*mid > x)
        {
            // 到左边找
            right = mid - 1;
        }
        else if (mid*mid < x)
        {
            // 到右边找
            left = mid + 1;
        }
        else
        {
            // 找到了
            return mid;
        }
    }
}

最后一个问题：如果“找不到”返回什么？一般来说，进行二分查找时，如果出了循环还没找到，此时就找不到了。但是这道题其实只是“类二分查找”，也就是说，找不到其实也是很正常的，因为有些数的算术平方根是小数。本质上你要找的是一个小数，但是却在一堆整数中找，当然找不到喽。举个例子：你要找的是7.5，mid就会逐渐逼近7.5，最后一次mid==7时，会执行left=mid+1，此时left就会变成8，并且left不会再变了，因为mid*mid<x已经没有机会了。所以，我们想返回的是7，最后left就一定是8，就应该返回left-1。

int mySqrt(int x){
	// [0,x]二分查找
    int left = 0;
    int right = x;
    while (left <= right)
    {
        // 求left和right的平均数
        int mid = left + (right-left) / 2;
        if (mid*mid > x)
        {
            // 到左边找
            right = mid - 1;
        }
        else if (mid*mid < x)
        {
            // 到右边找
            left = mid + 1;
        }
        else
        {
            // 找到了
            return mid;
        }
    }

    // left会跑到mid的右边，因为答案是mid的时候，mid的平方小于x
    return left - 1;
}

但这样过不了：

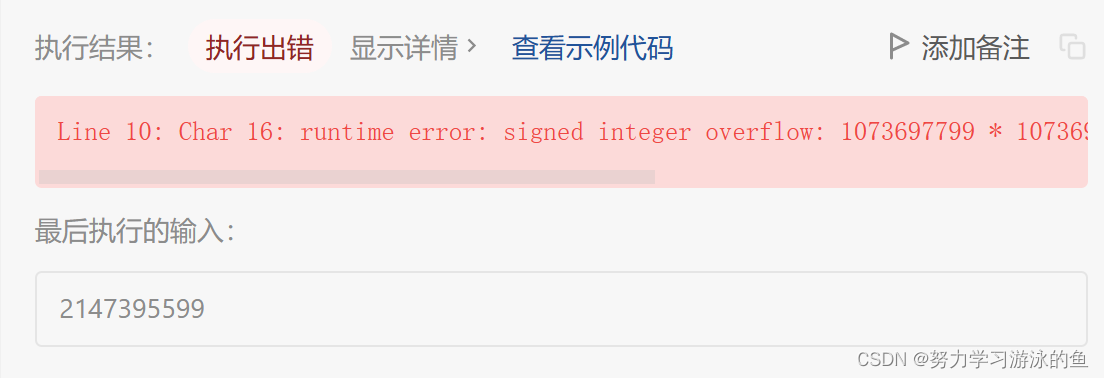
意料之中。因为这个数太大了，int存不下。这时，最简单的方法是把类型都改成long long，就可以了。

int mySqrt(int x){
	// [0,x]二分查找
    long long left = 0;
    long long right = x;
    while (left <= right)
    {
        // 求left和right的平均数
        long long mid = left + (right-left) / 2;
        if (mid*mid > x)
        {
            // 到左边找
            right = mid - 1;
        }
        else if (mid*mid < x)
        {
            // 到右边找
            left = mid + 1;
        }
        else
        {
            // 找到了
            return mid;
        }
    }

    // left会跑到mid的右边，因为答案是mid的时候，mid的平方小于x
    return left - 1;
}

不过毕竟类型不匹配，建议加上强制类型转换。

int mySqrt(int x){
    // [0,x]二分查找
    long long left = 0;
    long long right = x;
    while (left <= right)
    {
        // 求left和right的平均数
        long long mid = left + (right-left) / 2;
        if (mid*mid > (long long)x)
        {
            // 到左边找
            right = mid - 1;
        }
        else if (mid*mid < (long long)x)
        {
            // 到右边找
            left = mid + 1;
        }
        else
        {
            // 找到了
            return mid;
        }
    }

    // left会跑到mid的右边，因为答案是mid的时候，mid的平方小于x
    return (int)(left - 1);
}

这样就过了。

总结

1. 掌握二分查找，这是有序数组查找最好的方式。
2. 明白最后要返回啥，也就是left-1代表了啥。

感谢大家的阅读！