文章目录

前言
一、支持向量机简介
二、支持向量机的数学原理
- 1. 距离解算
- 2. 目标函数
- 3. 约束下的优化求解
- 4. 软间隔优化
- 5. 核函数变换
三、Python实现支持向量机
- 1. 惩罚力度对比
- 2. 高斯核函数
- 3. 非线性SVM
总结

前言

大部分传统的机器学习算法都可以实现分类任务，但这些模型关注的是将不同类别的数据分得开就行，也就是说它们的核心思想是让整个模型分类出错的损失越小越好。刚刚好有一种机器学习模型，它不仅关注分类能不能将不同类别的数据完全分得开，还关注分类得到的决策边界的间隔能不能最大化，即离该决策边界每个类别最近的数据点的距离能不能更远，这就是我们今天的主角 - - 支持向量机。

一、支持向量机简介

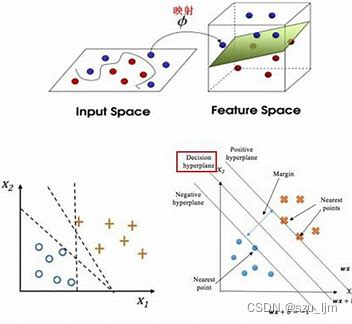
示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核变换，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

二、支持向量机的数学原理

在这里插入图片描述
支持向量机，从名字上来看它是由支持向量（Support Vectors）形成决策边界的一种模型，这里的支持向量是一种特殊的数据点，是所在类别数据中离决策平面最近的一些数据点，支撑起整个决策平面，有点像团队中骨干，他们支撑起整个团队的发展和未来。支持向量的个数与模型的复杂度成正比

1. 距离解算

与其他分类模型类似的是，支持向量机中我们用点到决策面的距离作为优化因子，我们以三维空间中的点到决策平面的距离计算原理推广到高维空间中

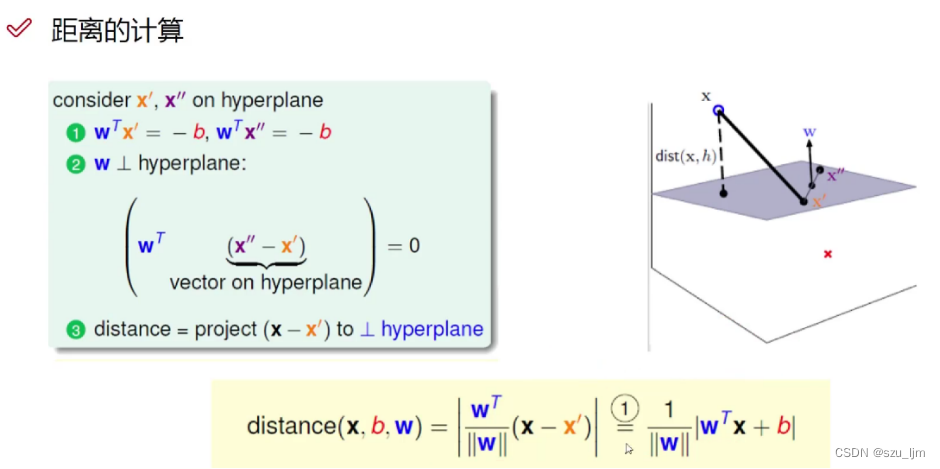
在这里插入图片描述
设决策平面方程为
$w^{T}x' + b = 0$

取任一数据点 $x$ ，设决策平面的法向量为 $w$ ，我们在决策平面上随便取一点 $x^{'}$ ，则 $x x^{'}$ 两点间的向量为 $x - x^{'}$ ，将向量 $x - x^{'}$ 与法向量 $w$ 作点乘可以算出向量 $x - x^{'}$ 在法向量 $w$ 上投影的长度（即点到平面距离）与法向量 $w$ 模的长度的乘积，再除以法向量 $w$ 模的长度得到点到平面距离，代入决策平面的方程消掉 $x^{'}$

$\frac{|w^{T}\cdot x+b|}{||w||}$

推广到高维空间中也同样适用，只是每个参数向量的维度都变高了
在这里插入图片描述
考虑到二分类模型要结合样本数据的标签，我们将正例的标签值定义为1，将负例的标签值定义为-1，对于给定的数据集 $M$ 和超平面 $w\cdot x+b=0$ ，定义超平面关于样本点 $\left( x_i,y_i \right)$ 的几何间隔为
$\frac{y_{i}(w^{T}\cdot x_{i}+b)}{||w||}$

在这里插入图片描述
接下来，我们按照原来的思路，对离决策平面最近的点的距离进行最大化为目标函数进行优化

2. 目标函数

我们假设离决策平面最近的点的距离为 $dis_{min}$ ，这个距离就是我们所谓的支持向量到超平面的距离。根据以上定义，SVM模型的求解最大分割超平面问题可以表示为的最优化问题的约束条件为
$\frac{y_{i}(w^{T}\cdot x_{i}+b)}{||w||} \geq dis_{min}$
最优化问题的目标函数为
$max_{w, b} dis_{min}$
在这里插入图片描述
为了对目标函数和约束条件进行简化，将约束条件两边同时除以 $dis_{min}$ ，放缩整合一下约束条件可以得出
$\frac{y_{i}(w^{T}\cdot x_{i}+b)}{||w||dis_{min}} \geq 1$
${y_{i}(w^{T}\cdot x_{i}+b)} \geq 1$

在这里插入图片描述
根据放缩推导可知， ${y_{i}(w^{T}\cdot x_{i}+b)} \geq 1$ 恒成立，又因为最大化 $dis_{min}$ 等价于最大化 $\frac{1}{||w||}$ ，所以目标函数和约束条件最终可以表达为
$min_{w, b} \frac{||w||^{2}}{2}$
${y_{i}(w^{T}\cdot x_{i}+b)} \geq 1$

3. 约束下的优化求解

拉格朗日乘子法是一种寻找多元函数在有约束条件下的极值的方法，结合拉格朗日乘子法我们可以构造新的目标函数，该目标函数是想求解在约束路径内，何种 $w, b, a$ 的组合下能使 $\frac{||w||^{2}}{2}$ 达到最小，其中 $\phi(x)$ 是核变换，是一种低维数据映射到高维的变换方式
$\frac{||w^{2}||}{2} - \sum_{i=1}^{n}\alpha(y_{i}(w^{T}\cdot \phi(x_{i})+b) - 1)$

在这里插入图片描述
按照拉格朗日乘子法的思想，接着目标函数分别对 $w, b, a$ 求偏导，并使三个偏导等于0，即可求得在约束条件下的极值恒等式，该恒等式表征了在约束条件下取极值时 $w, b$ 和 $\alpha$ 的关系，极值等式化简可以得到
$\frac{ \partial L }{ \partial w } = 0 \gg w = \sum_{i=1}^{n}\alpha y_{i} \phi(x_{i})$
$\frac{ \partial L }{ \partial b } = 0 \gg 0 = \sum_{i=1}^{n}\alpha y_{i}$

将极值恒等式代入目标函数消掉 $w, b$ ，即可得到关于 $\alpha$ 的一元目标函数

在这里插入图片描述
我们通过这个优化方法能得到 $\boldsymbol{\alpha }$ ，再根据 $\boldsymbol{\alpha }$ ，我们就可以求解出 $\boldsymbol{w} 和 \boldsymbol{b}$ ，进而求得我们最初的目的：找到超平面，即算出决策平面的方程。

4. 软间隔优化

现实生活中的数据往往是或本身就是非线性可分但是近似线性可分的，或是线性可分但是具有噪声的，以上两种情况都会导致在现实应用中，上面提到的硬间隔线性支持向量机变得不再实用。软间隔SVM中，我们的分类超平面既要能够尽可能地将数据类别分对，又要使得支持向量到超平面的间隔尽可能地大。
在这里插入图片描述
软间隔中 $\xi _i$ 为 “松弛变量”，即一个 $hin g e$ 损失函数。每一个样本都有一个对应的松弛变量，它表征该样本数据不满足约束的程度，不满足约束的程度越高该数据点越可能成为噪音点离群点。

软间隔的目标函数中 $C$ 称为正则化惩罚参数， $C$ 值越大，对分类的惩罚力度越大，容错率越低， $C$ 值越小，对分类的惩罚力度越小，容错率越高。后续跟线性可分求解的思路一致，同样这里先用拉格朗日乘子法得到拉格朗日函数，再求其对偶问题。

5. 核函数变换

在常见的二分类问题中，常常会出现低维数据不可分的问题，但如果只是简单地进行矩阵内积运算，又会出现新的问题 - - 维数灾难，即原始的空间为三维可以映射到20维，这也可以处理，但是如果我们低维的特征是100个维度，那需要更高的维度来映射，这时候映射成的维度是爆炸性增长的，计算量太大，无法计算了。支持向量机的优势主要体现在解决线性不可分问题，它通过引入核函数变换技巧，巧妙地解决了在高维空间中的内积运算，从而很好地解决了非线性分类问题。

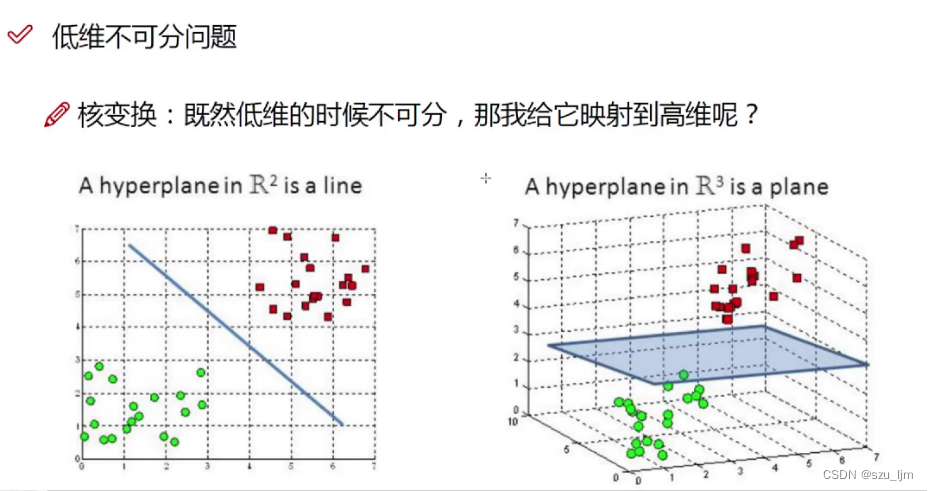
在这里插入图片描述
常用的核函数有

线性核函数(Linear Kernel)： $K (x, z) = x \cdot z$

多项式核函数(Polynomial Kernel)： $K (x, z) = (x \cdot z + 1) p$

高斯核函数(Gaussian Kernel)： $K(x,z)=e^{-\frac{|x-z|^{2}} {2 \sigma^{2}}}$

Sigmoid核函数(Sigmoid Kernel)： $K (x, z) = t anh （ γ x ∙ z + r)$

在这里插入图片描述
有了核函数我们就可以将低维线性不可分的数据映射到高维达到线性可分的效果，这就是非线性SVM的实现思想

三、Python实现支持向量机

1. 惩罚力度对比

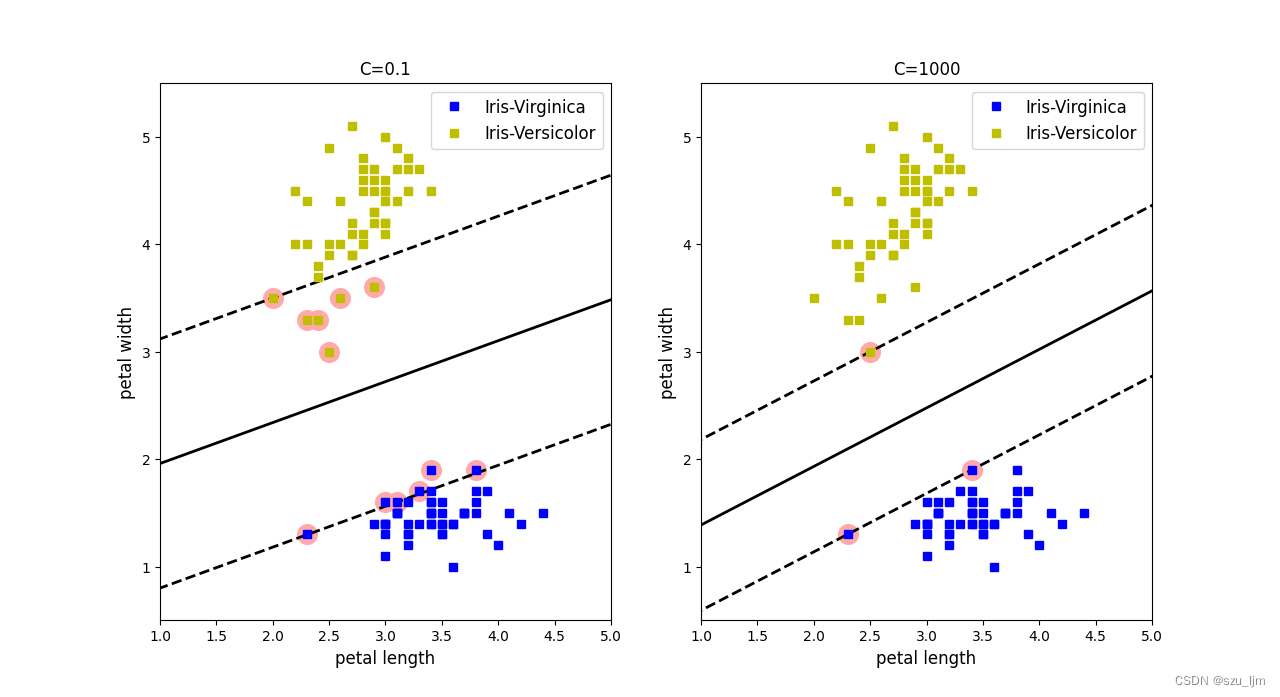
Python实现支持向量机的思路，首先导包，这次我们以鸢尾花数据集做实验，我们取鸢尾花数据集中两个特征和标签，接着实例化两个线性核的SVM，正则化参数C不同，然后定义决策平面和标出支持向量的函数等待调用，最后可视化展示一下

import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC
from sklearn.datasets import load_iris

iris = load_iris()
x = iris['data'][:, (1, 2)]
y = iris['target']

set_two_classes = (y==0) | (y==1)
x = x[set_two_classes]
y = y[set_two_classes]
svm_clf1 = SVC(kernel='linear', C=0.1)
svm_clf2 = SVC(kernel='linear', C=1000)
svm_clf1.fit(x, y)
svm_clf2.fit(x, y)

def plot_decision_boundary(svm_clf, xmin, xmax):
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]
    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin
    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=200, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, 'k-', linewidth=2)
    plt.plot(x0, gutter_up, 'k--', linewidth=2)
    plt.plot(x0, gutter_down, 'k--', linewidth=2)



plt.figure(figsize=(12, 8))
plt.subplot(121)
plot_decision_boundary(svm_clf1, 0, 6)
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], 'bs', label="Iris-Virginica")
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], 'ys', label="Iris-Versicolor")
plt.legend(loc="best", fontsize=12)
plt.xlabel("petal length", fontsize=12)
plt.ylabel("petal width", fontsize=12)
plt.title("C=0.1")
plt.axis([1, 5, 0.5, 5.5])
plt.subplot(122)
plot_decision_boundary(svm_clf2, 0, 6)
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], 'bs', label="Iris-Virginica")
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], 'ys', label="Iris-Versicolor")
plt.legend(loc="best", fontsize=12)
plt.xlabel("petal length", fontsize=12)
plt.ylabel("petal width", fontsize=12)
plt.title("C=1000")
plt.axis([1, 5, 0.5, 5.5])
plt.show()

在这里插入图片描述

2. 高斯核函数

Python实现高斯核映射的思路，首先导包，这次我们以随便生成的数据集做实验，定义高斯核函数的数学表达式和数据集画图函数，然后将数据代入高斯核函数计算，最后可视化展示一下

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D



x1 = np.linspace(-2, 2, 30)
y1 = np.sqrt(4 - 2 * x1**2)
x2 = np.linspace(-1, 1, 30)
y2 = np.sqrt(2 - 2 * x2**2)

colors = ["blue", "green"]
types = ["bs", "g^"]

def plot_dataset(x, y, ty):
    plt.plot(x, y, ty, markersize=3)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=12)
    plt.ylabel(r"$x_2$", fontsize=12, rotation=0)

# 定义高斯核函数
def gaussian_kernel(x1, y1, x2, y2, sigma=1):
    return np.exp(-((x1-y1)**2+(x2-y2)**2) / (2 * (sigma ** 2)))



# 计算高斯核函数矩阵
K1 = np.zeros((1, 30))
K2 = np.zeros((1, 30))
for i in range(1):
    for j in range(30):
       K1[i, j] = gaussian_kernel(x1[j], 0.0, y1[j], 1)
       K2[i, j] = gaussian_kernel(x2[j], 0.0, y2[j], 1)

# 画图
fig = plt.figure(figsize=(12, 8))

ax1 = fig.add_subplot(121)
plot_dataset(x1, y1, types[0])
plot_dataset(x2, y2, types[1])
ax2 = fig.add_subplot(122, projection='3d')
ax2.scatter(x1.flatten(), y1.flatten(), K1.flatten(), c=colors[0], cmap='rainbow')
ax2.scatter(x2.flatten(), y2.flatten(), K2.flatten(), c=colors[1], cmap='rainbow')
plt.show()

在这里插入图片描述
可以清晰地看见，在二维空间中线性不可分的数据映射到三维空间中就变得线性可分了

3. 非线性SVM

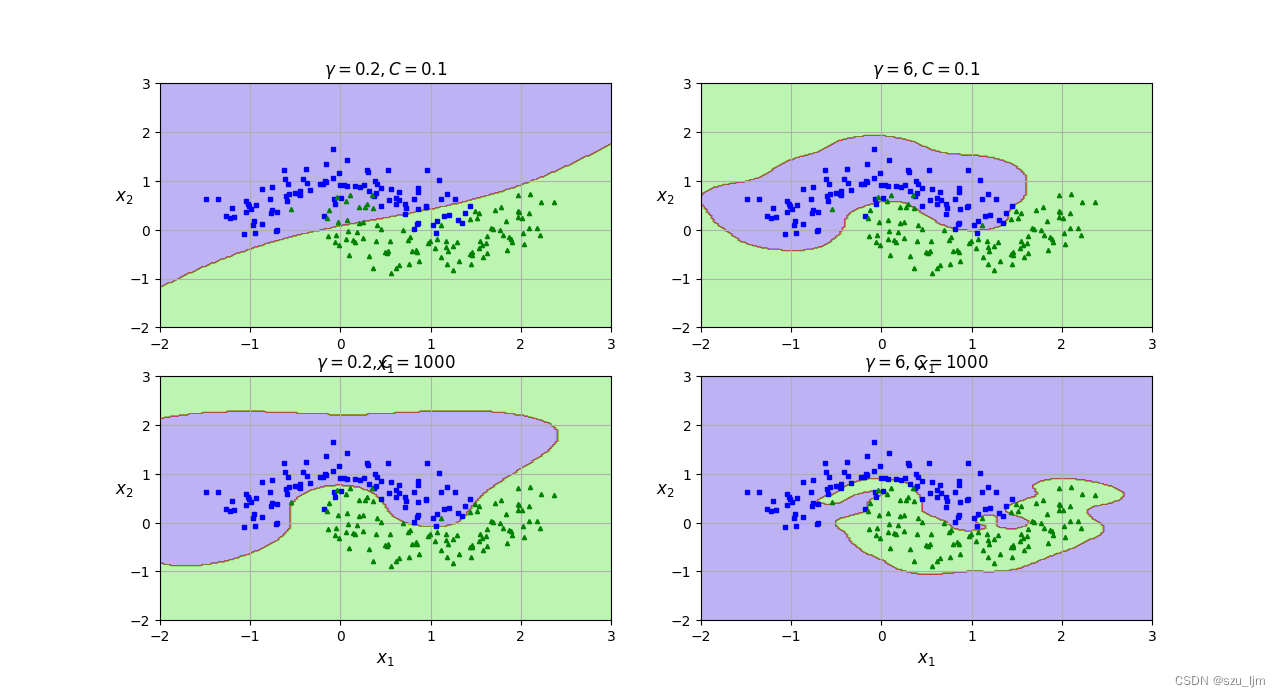
Python实现非线性SVM的思路，首先导包，这次我们以月亮数据集做实验，我们取月亮数据集中两个特征和标签，接着实例化两个高斯核的SVM，在正则化参数C不同， $\gamma$ 参数不同的情况下作对比，然后定义决策平面和标出支持向量的画图函数等待调用，最后枚举画图可视化展示一下

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

x, y = make_moons(n_samples=200, noise=0.23, random_state=36)
gamma1, gamma2 = 0.2, 6
C1, C2 = 0.1, 1000
hyperparams = (gamma1, C1), (gamma2, C1), (gamma1, C2), (gamma2, C2)
svm_clfs = []

def plot_dataset(x, y):
    plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], "bs", markersize=3)
    plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], "g^", markersize=3)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=12)
    plt.ylabel(r"$x_2$", fontsize=12, rotation=0)

def plot_predictions(svm_clf):
    x0 = np.linspace(-2, 3, 200)
    x1 = np.linspace(-2, 3, 200)
    x0s, x1s = np.meshgrid(x0, x1)
    X = np.c_[x0s.ravel(), x1s.ravel()]
    y_pred = svm_clf.predict(X).reshape(x0s.shape)
    plt.contourf(x0s, x1s, y_pred, cmap=plt.cm.brg, alpha=0.3)

for gamma, C in hyperparams:
    rbf_svm_clf = Pipeline([("scaler", StandardScaler()),("svm_clf", SVC(kernel="rbf" ,C=C, gamma=gamma))])
    rbf_svm_clf.fit(x, y)
    svm_clfs.append(rbf_svm_clf)


plt.figure(figsize=(12, 8))

for i, svm_clf in enumerate(svm_clfs):
    plt.subplot(221+i)
    plot_predictions(svm_clf)
    plot_dataset(x, y)
    gamma, C = hyperparams[i]
    plt.title(r"$\gamma = {},C = {}$".format(gamma, C), fontsize=12)
plt.show()