1 说在前面

本文的主要内容来自于Unity引擎中Spline功能的一个函数，一开始我难以理解这几个向量运算的作用和几何意义，经过一番思考后总结如下：
该段代码实际上更像是两个直线之间寻找最短距离，然后判断该距离对应的点在其中一条直线（代码中称为线段）上的位置（线段前、线段中、线段后）；由于代码中以射线-线段的关系来描述这个问题，本文中也统一以射线和线段称呼两者的关系，在以后再次提到时就不做补充说明了；

函数的具体内容为：

/// <summary>
/// Returns the parameterization of a ray line projection. The parameter will be negative if the nearest point
/// between the ray/line is negative to 'lineOrigin', and greater than 1 if nearest intersection is past the end
/// off the line segment (lineOrigin + lineDir).
/// </summary>
/// <param name="ro">The ray origin point.</param>
/// <param name="rd">The ray direction (normalized vector).</param>
/// <param name="lineOrigin">Line segment first point.</param>
/// <param name="lineDir">Line segment direction (with magnitude).</param>
/// <returns>The parameter of a ray line projection.</returns>
public static float RayLineParameter(float3 ro, float3 rd, float3 lineOrigin, float3 lineDir)
{
    var v0 = ro - lineOrigin;
    var v1 = math.cross(rd, math.cross(rd, lineDir));
    // the parameter of a ray to line projection will be negative if the intersection is negative to line
    // direction from 'a', and greater than 1 if intersection is past the line segment end 'b'
    return math.dot(v0, v1) / math.dot(lineDir, v1);
}

该函数实现了：输入一个射线的起点与方向：ro、rd，以及一个线段的起点和朝向（包括了线段的长度）。返回一个float数值，表示射线到线段的最小距离对应的点在线段上的位置，（0-1）之间表示在线段上，（-∞，0）表示在线段起点之前，(0, +∞)表示在线段重点之，该数值约接近0表示距离线段起点越近，越接近1表示距离线段终点越近。一些特例如下图所示：

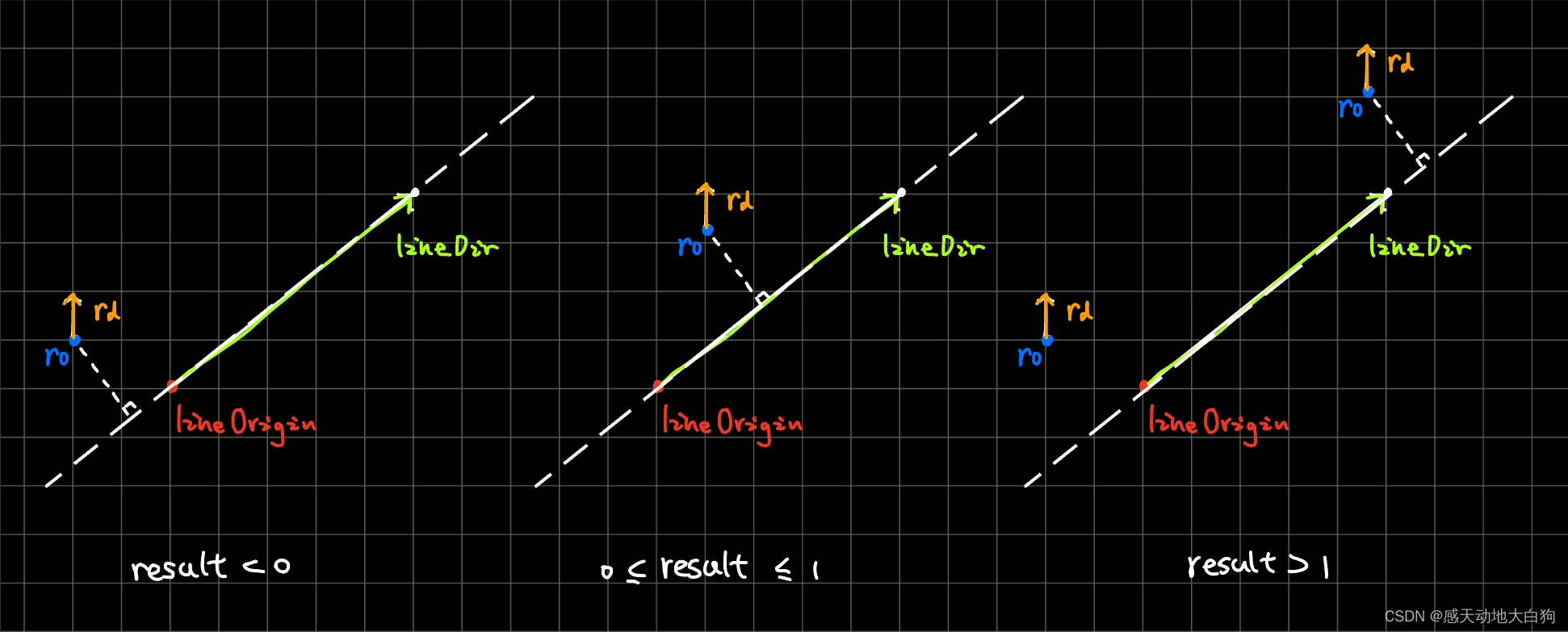
需要注意，射线和线段都是用float3表示的，它们存在于三维空间中，以上例子只不过是刚好同处于一个二维平面下的特例。

2 运算

该计算涉及两个向量：射线向量和线段向量，分别用a和l表示，进一步的，将向量的首末端点表示为$a_0,a_1$和$l_0,l_1$，如下图所示：

这段代码其实很短，只计算了两个中间变量$v_0,v_1$，随后进行了返回值的计算；
①$v_0$：意义非常明显，表示为向量$Vector(l_0,r0)$，如下图所示：

②$v_1$：则相对复杂一点，其经过了两次向量叉乘，首先：
$r_d\times lineDir$：获得一个与射线和线段都垂直的向量，即与$Vector(r_0,r_1)$和$Vector(l_0,l_1)$都垂直的向量；
$r_d\times （r_d\times lineDir）$：在此基础上又将该向量和$r_d$叉乘得到中间向量$v_1$;
上述整个过程如下图所示：

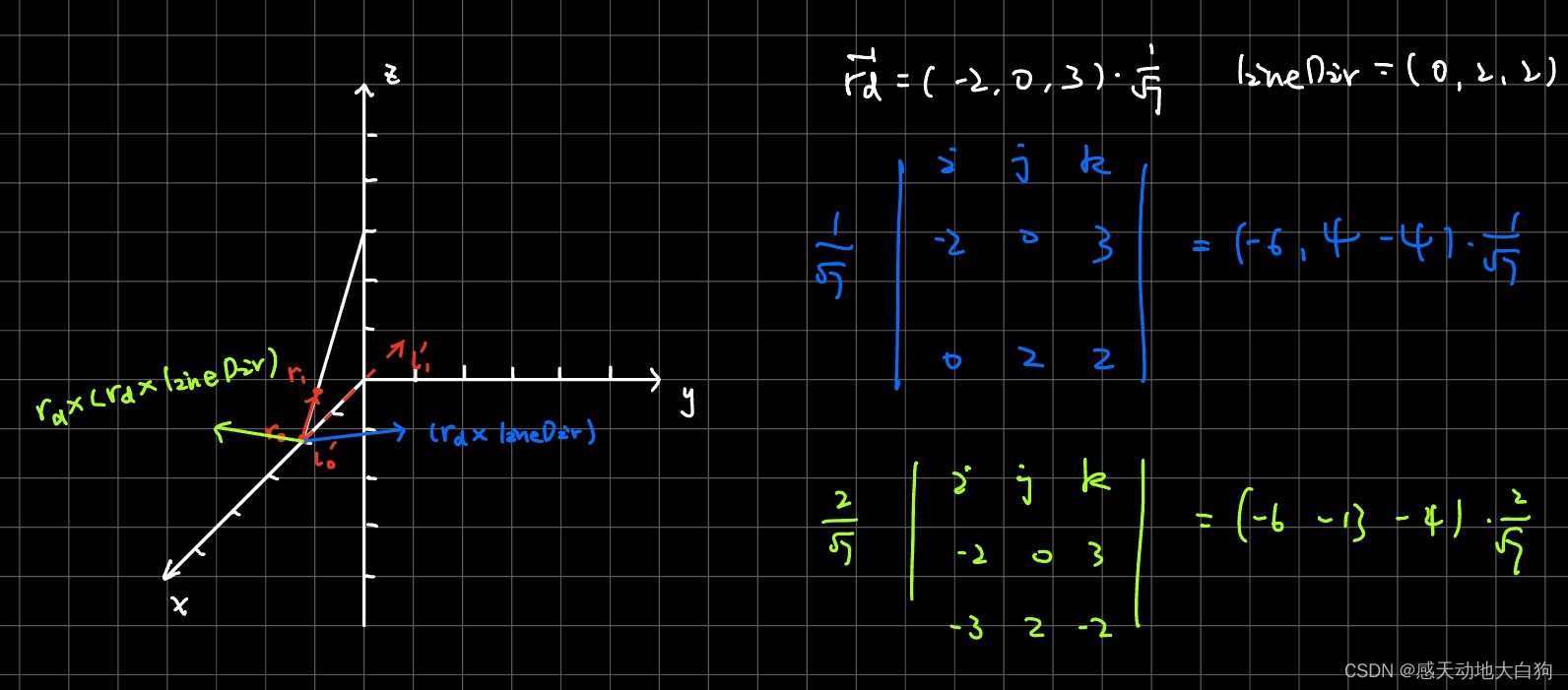
仔细观察，可以发现$v_1$与$r_d$和$lineDir$是共面的，因为$r_d\times lineDir$垂直于$r_d$和$lineDir$所在平面，再与$r_d$叉乘后的结果又回到了$r_d$和$lineDir$所在平面。
③result：返回值通过中间计算量得到，有：
$$result=\frac{v_0\cdot v_1}{lineDir\cdot v_1}$$几何关系如下图所示

3 原理

3.1 坐标系变换

result为何具备文章开头时所说的几何意义呢，仔细观察可以发现，该计算结果可以换个视角，将$v_1$与$r_d$和$lineDir$所在平面视作yoz平面，其中$r_d$指向z轴方向，$v_1$指向y轴负方向，result的计算可以转化为下图中右侧的部分：

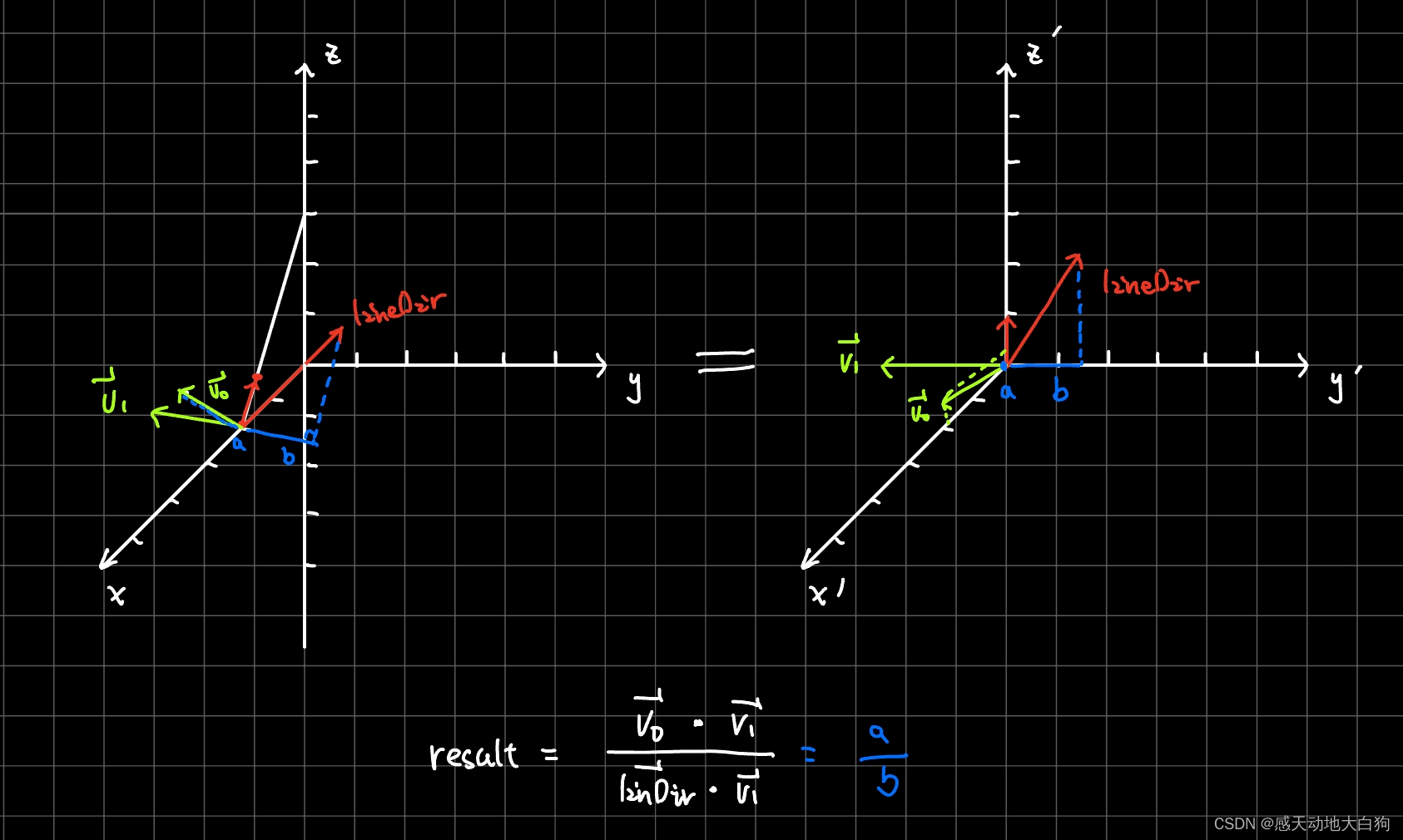
注意！注意！注意！向量$v_0$是不在yoz平面上的！，从这个新的坐标系理解
result：代表了$v_0$和$lineDir$在新y轴上的投影结果a、b的比值，只不过本文例子中a刚好为0；此时result=0，表示射线到线段的最短点刚好为线段的起点。

3.2 为什么是y轴上投影

我们来看$v_0$的变化对结果的影响，先简单地将射线和线段起点重合，此时很容易看出，射线到线段上最短距离对应的点就是原点，距离为0，如下图所示：

将目标线段沿着x’轴移动，发现最短的点仍然为线段的原点，射线上对应的仍然是原点，只不过最短距离发生了变化，也就是说在x’方向上的距离分量是无法通过调整射线上和线段上点的位置缩短的，其增减的是不可更改的距离，如下图所示：

同样的，将目标线段沿着z’轴移动，发现最短的点仍然为线段的原点，最短距离也没有发生变化，只不过射线上对应的点改变了，也就是说在z’方向上的距离分量是可以通过调整射线上点的位置抵消的，如下图所示：

最后，将目标线段沿着y’轴移动，发现最短的点在线段上的位置改变了，分别在线段终点后，线段上和线段起点前，射线上对应的点也改变了，但是最短距离没有改变，这就是为什么需要y轴上的投影了；

3.3 result的几何意义

为什么result能够描述最近点在目标线段什么位置呢？先看下图：

可以看出，只有当线段落在lineLeft和lineRight之间时（不考虑x、z轴的变化），射线和线段之间的最短距离点才会落在线段上，而lineLeft和lineRight之间的长度正是$lineDir\cdot v_1$，即result的 分母；
曲线再往左或者再往右对应了最短距离点再线段的哪一侧，result的几何意义就是这样。

4 总结

①射线的方向向量和线段的方向向量构成了一个新的参考坐标系x’y’z’，该坐标系中射线方向向量是y轴，两个方向向量在yoz平面上；
②result的分母，也就是b只和两个因素有关：两个方向向量的夹角、以及线段长度；这很好理解：
1、当两个向量夹角越小，线段上点到射线上一点的跨度就越小，反之跨度越大。因此夹角越小时最短距离点在线段上的可能越小，反之亦然；
2、线段越长，最短距离点在线段上的可能性越大；
③result的分子，也就是a只与射线和线段的起点构成的距离向量相关，且该距离向量在新坐标系下x、z轴上的分量是不影响结果的；