Python每日一练(20230507) 丑数I\II\III、超级丑数

news2024/11/16 5:22:59

1. 丑数 Ugly Number I

2. 丑数 Ugly Number II

3. 丑数 Ugly Number III

4. 超级丑数 Super Ugly Number

🌟 每日一练刷题专栏 🌟

Golang每日一练专栏

Python每日一练专栏

C/C++每日一练专栏

Java每日一练专栏

1. 丑数 Ugly Number I

丑数就是只包含质因数 2、3 和 5 的正整数。

给你一个整数 n ，请你判断 n 是否为丑数。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：n = 6
输出：true
解释：6 = 2 × 3

示例 2：

输入：n = 1
输出：true
解释：1 没有质因数，因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。

示例 3：

输入：n = 14
输出：false
解释：14 不是丑数，因为它包含了另外一个质因数 7 。

提示：

-2^31 <= n <= 2^31 - 1

代码：

class Solution:
    def isUgly(self, n: int) -> bool:
        if n <= 0:
            return False
        for i in [2, 3, 5]:
            while n % i == 0:
                n //= i
        return n == 1

# %%
s = Solution()
print(s.isUgly(6))
print(s.isUgly(1))
print(s.isUgly(14))

for i in range(1,21):
    s = Solution()
    if s.isUgly(i):
        print(i, end=" ")

递归写法：

class Solution:
    def isUgly(self, n: int) -> bool:
        if n <= 0:
            return False
        elif n == 1:
            return True
        elif n % 2 == 0:
            return self.isUgly(n // 2)
        elif n % 3 == 0:
            return self.isUgly(n // 3)
        elif n % 5 == 0:
            return self.isUgly(n // 5)
        else:
            return False
# %%
s = Solution()
print(s.isUgly(6))
print(s.isUgly(1))
print(s.isUgly(14))

for i in range(1,21):
    s = Solution()
    if s.isUgly(i):
        print(i, end=" ")

输出：

True
True
False
1 2 3 4 5 6 8 9 10 12 15 16 18 20

2. 丑数 Ugly Number II

给你一个整数 n ，请你找出并返回第 n 个丑数。

丑数就是只包含质因数 2、3 和/或 5 的正整数。

示例 1：

输入：n = 10
输出：12
解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。

示例 2：

输入：n = 1
输出：1
解释：1 通常被视为丑数。

提示：

1 <= n <= 1690

代码：

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        nums = [1]
        p_2, p_3, p_5 = 0, 0, 0
        for i in range(1, n):
            nums.append(min(nums[p_2]*2, nums[p_3]*3, nums[p_5]*5))
            if nums[-1] == nums[p_2]*2:
                p_2 += 1
            if nums[-1] == nums[p_3]*3:
                p_3 += 1
            if nums[-1] == nums[p_5]*5:
                p_5 += 1
        return nums[-1]

# %%
s = Solution()
print(s.nthUglyNumber(10))
print(s.nthUglyNumber(1))

for i in range(1,15):
    print(s.nthUglyNumber(i), end=" ")

调用上题函数：

class Solution:
    def isUgly(self, n: int) -> bool:
        if n <= 0:
            return False
        for i in [2, 3, 5]:
            while n % i == 0:
                n //= i
        return n == 1
    def nthUglyNumber(self, n: int) -> int:
        count = 0
        i = 1
        while count < n:
            if self.isUgly(i):
                count += 1
            if count == n:
                return i
            i += 1
        return -1

# %%
s = Solution()
print(s.nthUglyNumber(10))
print(s.nthUglyNumber(1))

for i in range(1,15):
    print(s.nthUglyNumber(i), end=" ")

输出：

12
1
1 2 3 4 5 6 8 9 10 12 15 16 18 20

3. 丑数 Ugly Number III

给你四个整数：n 、a 、b 、c ，请你设计一个算法来找出第 n 个丑数。

丑数是可以被 a 或 b 或 c 整除的 正整数 。

示例 1：

输入：n = 3, a = 2, b = 3, c = 5
输出：4
解释：丑数序列为 2, 3, 4, 5, 6, 8, 9, 10... 其中第 3 个是 4。

示例 2：

输入：n = 4, a = 2, b = 3, c = 4
输出：6
解释：丑数序列为 2, 3, 4, 6, 8, 9, 10, 12... 其中第 4 个是 6。

示例 3：

输入：n = 5, a = 2, b = 11, c = 13
输出：10
解释：丑数序列为 2, 4, 6, 8, 10, 11, 12, 13... 其中第 5 个是 10。

示例 4：

输入：n = 1000000000, a = 2, b = 217983653, c = 336916467
输出：1999999984

提示：

1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内

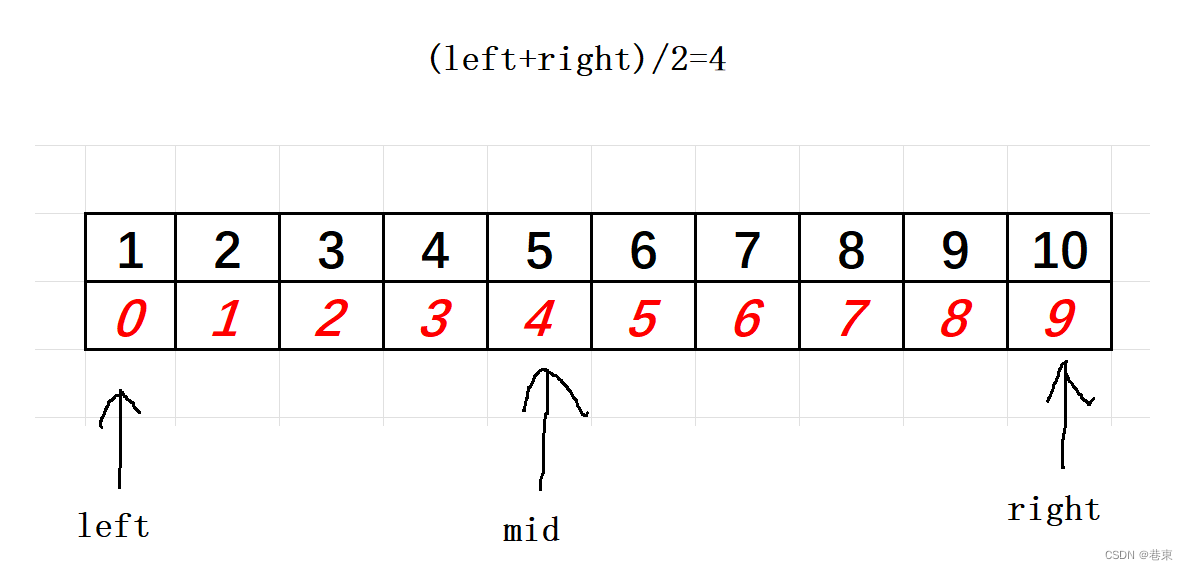
代码： 二分查找

class Solution:
    def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:
        def gcd(x, y):
            return x if y == 0 else gcd(y, x % y)

        def lcm(x, y):
            return x // gcd(x, y) * y

        left, right = 1, 2 * 10**9
        ab_lcm, ac_lcm, bc_lcm, abc_lcm = lcm(a, b), lcm(a, c), lcm(b, c), lcm(lcm(a, b), c)

        while left < right:
            mid = left + (right - left) // 2
            cnt = mid // a + mid // b + mid // c - mid // ab_lcm - mid // ac_lcm - mid // bc_lcm + mid // abc_lcm
            if cnt < n:
                left = mid + 1
            else:
                right = mid
        return left

# %%
s = Solution()
print(s.nthUglyNumber(n = 3, a = 2, b = 3, c = 5))
print(s.nthUglyNumber(n = 4, a = 2, b = 3, c = 4))
print(s.nthUglyNumber(n = 5, a = 2, b = 11, c = 13))

print(s.nthUglyNumber(n = 1000000000, a = 2, b = 217983653, c = 336916467))

输出：

4
6
10
1999999984

4. 超级丑数 Super Ugly Number

超级丑数 是一个正整数，并满足其所有质因数都出现在质数数组 primes 中。

给你一个整数 n 和一个整数数组 primes ，返回第 n 个 超级丑数 。

题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。

示例 1：

输入：n = 12, primes = [2,7,13,19]
输出：32 
解释：给定长度为 4 的质数数组 primes = [2,7,13,19]，前 12 个超级丑数序列为：[1,2,4,7,8,13,14,16,19,26,28,32] 。

示例 2：

输入：n = 1, primes = [2,3,5]
输出：1
解释：1 不含质因数，因此它的所有质因数都在质数数组 primes = [2,3,5] 中。

提示：

1 <= n <= 10^6
1 <= primes.length <= 100
2 <= primes[i] <= 1000
题目数据保证 primes[i] 是一个质数
primes 中的所有值都 互不相同 ，且按 递增顺序 排列

代码：

from typing import List
class Solution:
    def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:
        dp = [1] * n
        k = len(primes)
        pointers = [0] * k
        for i in range(1, n):
            choices = [dp[pointers[j]] * primes[j] for j in range(k)]
            dp[i] = min(choices)
            for j in range(k):
                if dp[pointers[j]] * primes[j] == dp[i]:
                    pointers[j] += 1
        return dp[-1]

# %%
s = Solution()
print(s.nthSuperUglyNumber(n = 12, primes = [2,7,13,19]))
print(s.nthSuperUglyNumber(n = 1, primes = [2,3,5]))

输出：

32
1