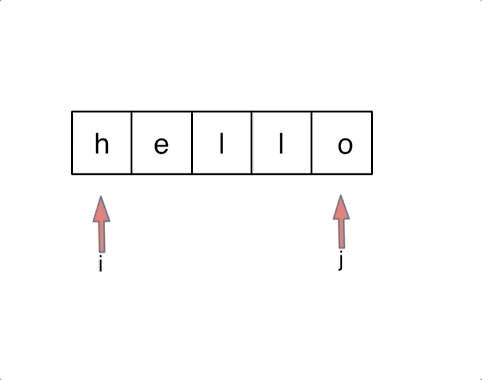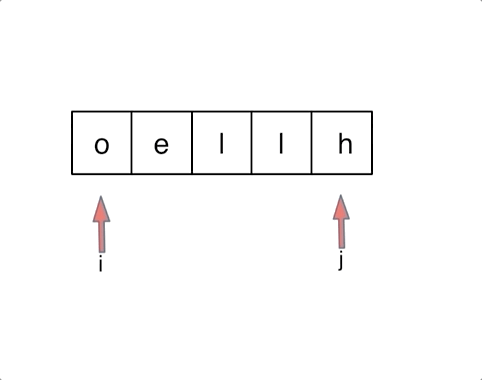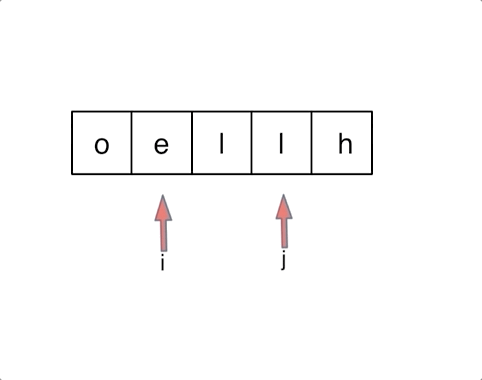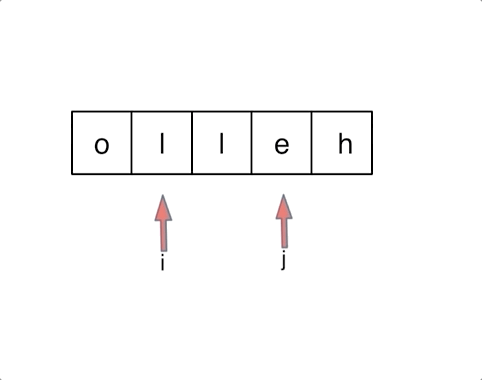
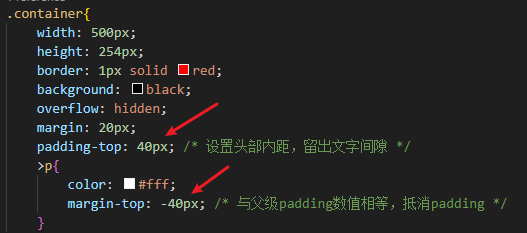
相当的惨烈，乱交

Q1

前后缀分解,用set统计不同元素的个数

class Solution {
   public:
    vector<int> distinctDifferenceArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> L(n + 1, 0), R(n + 1, 0);  // 前缀不同数的个数
        set<int> s;
        for (int i = 0; i < n; i++) {
            s.insert(nums[i]);
            L[i] = s.size();
        }
        s.clear();
        for (int i = n - 1; i >= 0; i--) {
            s.insert(nums[i]);
            R[i] = s.size();
        }
        vector<int> ans(n);
        for (int i = 0; i < n; i++) {
            ans[i] = L[i] - R[i + 1];
        }
        return ans;
    }
};

Q2

用两个哈希表来计数。

遍历会超时,所以得另开一个哈希表统计出现的次数，但是更新时要同时更新次数。

用数组桶计数也可以因为数据小。

class FrequencyTracker {
   public:
    unordered_map<int, int> mp;
    unordered_map<int, int> count;
    FrequencyTracker() {
        mp.clear();
    }

    void add(int number) {
        if(mp[number] > 0)
            count[mp[number]]--;
        mp[number]++;
        count[mp[number]]++;
    }

    void deleteOne(int number) {
        if (mp[number] != 0){
            count[mp[number]]--;
            mp[number]--;
            count[mp[number]]++;
        }
    }

    bool hasFrequency(int frequency) {
        return count[frequency] > 0;
    }
};

Q3

贪心，考虑修改颜色之后，答案的增减情况，相邻有两种情况

1. 原来就已经相等
   • 修改后还是相等，那么答案不变
   • 修改后判断前后是否改变，改变答案-1
2. 原来不相等，修改后相等
   • 如果和前面相等答案+1
   • 如果和后面相等答案+1

class Solution {
   public:
    vector<int> colorTheArray(int n, vector<vector<int>>& queries) {
        vector<int> color(n, 0);
        vector<int> ans(queries.size(), 0);
        ans[0] = 0;
        color[queries[0][0]] = queries[0][1];
        for (int i = 1; i < queries.size(); i++) {
            int index = queries[i][0], c = queries[i][1];
            if (c == color[index]) { // 改不改都一样
                ans[i] = ans[i - 1];
                continue;
            }
            // 修改前相邻的相等
            int cur = color[index];
            if (index > 0 && color[index - 1] == cur && color[index - 1] != 0) {
                ans[i] -= 1;
            }
            if (index + 1 < n && color[index + 1] == cur && color[index + 1] != 0) {
                ans[i] -= 1;
            }
            color[index] = c;
            // 修改后相邻的相等
            if (index > 0 && color[index - 1] == c && color[index - 1] != 0) {
                ans[i] += 1;
            } 
            if (index + 1 < n && color[index + 1] == c && color[index + 1] != 0) {
                ans[i] += 1;
            }
            ans[i] += ans[i - 1];
        }
        return ans;
    }
};

Q4

要使得根节点到叶子节点路径都相等，那么每一个父节点到叶节点的路径也相等，那么就是把左右子节点的值改成一样，修改次数就是两子节点的差值。

class Solution {
   public:
    int sum = 0;  // 求每个父节点左右子节点abs差值的和,父节点的值为左右子节点的最大值+cost[u]
    int dfs(int u, vector<int>& cost) {
        if (u >= cost.size()) return 0;
        int l = dfs(2 * u + 1, cost);
        int r = dfs(2 * u + 2, cost);
        sum += abs(l - r);
        cost[u] += max(l, r);  
        return cost[u];
    }
    int minIncrements(int n, vector<int>& cost) {
        dfs(0, cost);
        return sum;
    }
};