一、为什么选择四元数
描述两个坐标系之间的变换关系主要有几个方法
1、欧拉角法(存在奇异性和万向锁而且三个轴旋转的顺序不好定)
2、方向余弦矩阵法(翻译为Directional cosine matrix，简称DCM，也称为旋转矩阵，看了很多博客写的是C11-C33的那个矩阵，没明白为什么也称之为一个方法，有知道的指导一下，这里就不深入去看了)
3、四元数法(不容易理解，多一个维度)
动态欧拉角指的是旋转的过程当中，坐标轴跟着变化，静态的则是旋转的时候坐标轴不变。我个人理解为，当世界坐标系为参考系的情况下，物体三维旋转，是静态欧拉角，自身为参考系的情况下，是动态欧拉角，这种情况下旋转某个轴，另外的轴会改变方向。
选择四元数方法表示姿态(表示角度旋转变换的状态)，是由于动态欧拉角，在旋转的过程中存在万向锁的情况，不适合随意旋转，并且有奇异性，不能够灵活的表示姿态，并且四元数更适合插值。(不过要注意的是，每次四元数插值结果都要进行规范化！！)
动态与静态欧拉角视角下的万向节死锁（Gimbal Lock）问题
四元数法比欧拉角法和余弦向量法相比有哪些优势？
gimbal lock到底是个什么东西？
四元数和欧拉角优缺点
万向锁(Gimbal lock)问题的理解及解决 RobotSlam
万向节死锁的本质 Gimbal Lock
<此处结论是就用四元数来表征计算旋转关系以及坐标系变换计算>
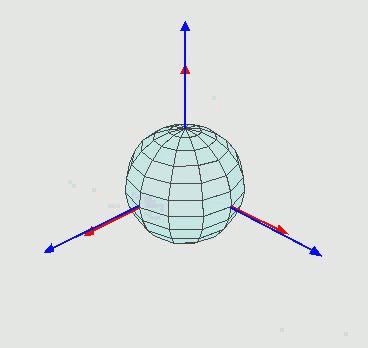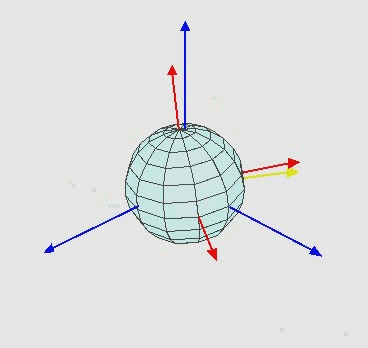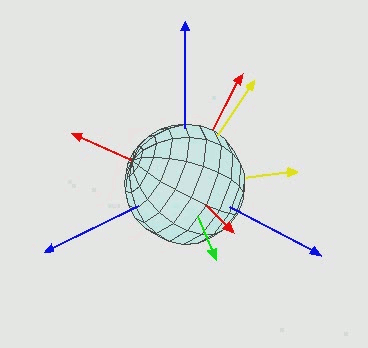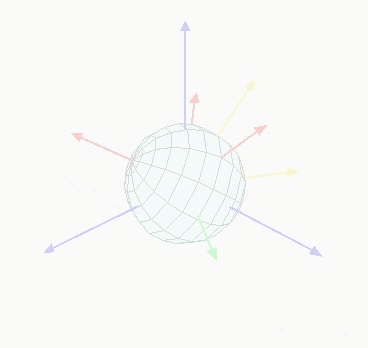
图片地址
二、旋转矩阵推导
以下两篇文章中写的特别详细，欧拉角和旋转矩阵的推导，尤其是其中先看绕一个轴进行旋转得到的旋转关系矩阵，然后根据三个轴的推导出任意的旋转关系矩阵(Z-Y-X旋转顺序)。
姿态解算（五）四元数、欧拉角、方向余弦矩阵
四元数、欧拉角和方向余弦的定义及关系
惯性组合导航原理—[1] 方向余弦矩阵
导航坐标系(参考坐标系，地理坐标系)n，选取东北天右手直角坐标系作为导航坐标系n、载体坐标系(机体坐标系)b，绕Z轴旋转偏航角(YAW)、绕Y轴旋转横滚角(ROLL)、绕X轴旋转俯仰角(PITCH)
选取右手直角坐标系定义：四轴向右为X正方向，向前为Y轴正方向，向上为Z轴正方向。
下面公式为一个坐标系绕着其本身的XYZ轴旋转的矩阵，单轴旋转的矩阵。
X轴：
Y轴：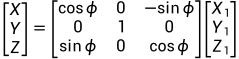
Z轴：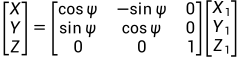
对应矩阵也叫做givens矩阵(是正交矩阵，秩为1)，[矩阵的QR分解系列二] 吉文斯(Givens)变换
绕着Z-X-Y轴旋转得到如果公式(先旋转的先左乘，矩阵更贴近[X Y Z])：
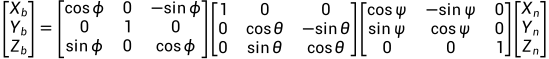
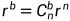
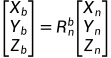
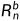为坐标系n到坐标系b的变换矩阵，我们平常定义的欧拉角形式的方向余弦矩阵为 
，
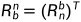这两个图中公式就是欧拉角形式的坐标系变换矩阵，旋转矩阵一定注意是从哪个坐标系到哪个坐标系的旋转。
点击查看欧拉角旋转矩阵图
欧拉角旋转矩阵公式图
四元数
我们想要使用四元数表征旋转，既然四元数可以灵活的表示姿态，那么可以我们可以先用四元数表征两个状态，继而通过两个姿态状态的变化推导出坐标系变换矩阵，达到和欧拉角表示的相通的目的。
惯性组合导航原理—[2] 用四元数表征旋转
四元数旋转矩阵公式图
四元数对应的旋转矩阵有了，欧拉角形式的旋转矩阵也有了，对应旋转方向统一，两者关系就可以求出来了。
四元数表示三个旋转角的公式
反对称阵
当三维坐标点发生旋转时，如果采用矩阵运算就会需要考虑“左乘”和“右乘”。若绕静坐标系（世界坐标系）旋转，则左乘，也是变换矩阵*坐标矩阵；若是绕动坐标系旋转（自身建立一个坐标系），则右乘，也就是坐标矩阵*变换矩阵。但现实中，我们只是对一个图像、点云进行旋转，则均是左乘实现
这里我的理解是和静欧拉角和动欧拉角能够对应的，基本的旋转形态对应，即参考系为静坐标系还是自身的坐标系。 三维变换矩阵左乘和右乘分析 旋转的左乘与右乘
我从此文学习了反对称矩阵的作用，此文通过对两个向量叉乘，推导出外积可以用反对称矩阵计算的例子。惯性组合导航原理—[2] 用四元数表征旋转 -- csdn zytjasper
反对称阵可以用点乘运算代替叉乘运算，V1和V2的外积，等于V1的反对称阵和V2做内积(叉乘变点乘)
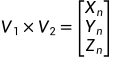
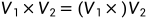
三、姿态解算部分
借用王尼莫前辈博客里面的一句话，四旋翼飞行器的姿态解算小知识点 王尼莫
姿态的数据来源有5个：重力、地磁、陀螺仪、加速度计、电子罗盘。其中前两个来自“地理”坐标系，后三个来自“载体”坐标系。
我们的目的是计算四元数来表征我们的姿态，在二中我们已经得到了通过四元数表征角度的公式，接下来只需要每次得到准确的四元数即可。
然而需要对误差校正以及补偿，要进行补偿计算，首先要将补偿值和被补偿值都换算到同一坐标系下。
[0 0 1] 为n系中的重力加速度，
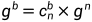
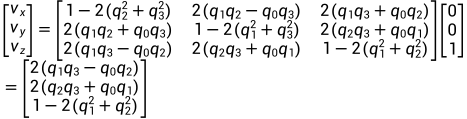
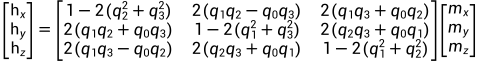
读取到的加速度计测量值是ax,ay,az，陀螺仪的测量值是wx,wy,wz，磁力计的测量值是mx,my,mz。
将三个测量值都转化为单位向量(加速度计值转换为单位向量容易和b系下的[0 0 1]运算)。
参考资料：
为什么选择四元数：
动态与静态欧拉角视角下的万向节死锁（Gimbal Lock）问题
四元数法比欧拉角法和余弦向量法相比有哪些优势？
gimbal lock到底是个什么东西？
四元数和欧拉角优缺点
万向锁(Gimbal lock)问题的理解及解决 RobotSlam
万向节死锁的本质 Gimbal Lock
四元数和其他两种表示方式的相互推导关系：
姿态解算（五）四元数、欧拉角、方向余弦矩阵
四元数、欧拉角和方向余弦的定义及关系 wust_fly_high
欧拉角到方向余弦矩阵 darcsdn
反对称矩阵作用(计算中的数学知识以及为什么使用四元数和什么是四元数)：
惯性组合导航原理—[2] 用四元数表征旋转 -- csdn zytjasper
有问题表述不清请多交流，有错误请务必指出，侵删联系，随意引用，谢谢(立个Flag，把大学和研究生期间的数据捡一捡，发现工作后接触到的数学都是以前学过的，某些知识细节可以再刷刷深入理解下)。
int mx,my,mz;
int ax,ay,az;
//互补滤波是这样的：陀螺积分角度+=角速度*dt；
//融合角度=陀螺权值*陀螺积分角度+(1-陀螺权值)*加速度角度；还有一种叫最大梯度法的，就是你发的这段代码
//大概是这样的： 陀螺积分角度+=角速度*dt；角度偏差=加速度角度-陀螺积分角度；
//融合角度=陀螺角度+衰减系数*角度偏差；用来矫正陀螺本身的静态漂移：角度偏差积分+=角度偏差；角速度=角速度+衰减系数*角度偏差积分；
//这个就可以一定程度上矫正陀螺的零漂。
//下面这幅图才是准确的阐述了互补滤波的过程。正常情况下用陀螺仪的数据就可以进行姿态的更新，
//但是由于陀螺仪的积分误差，这里用acc和mag去校正，求出他们的误差用PI去弥补。
//注意看看pid的公式和作用，pid是作用于误差（实际个期望之间的差值），最终反复调节，让实际值=期望值。
// 加速度计、地磁计、陀螺仪数据融合，更新四元数
/*
[gx,gy,gz]为陀螺仪的测量值
[ax,at,az]为加速度的测量值
[mx,my,mz]为地磁计的测量值
*/
/*
*AHRS
*/
// AHRS.c
// Quaternion implementation of the 'DCM filter' [Mayhony et al]. Incorporates the magnetic distortion
// compensation algorithms from my filter [Madgwick] which eliminatesthe need for a reference
// direction of flux (bx bz) to be predefined and limits the effect ofmagnetic distortions to yaw
// axis only.
// User must define 'halfT' as the (sample period / 2), and the filtergains 'Kp' and 'Ki'.
// Global variables 'q0', 'q1', 'q2', 'q3' are the quaternion elementsrepresenting the estimated
// orientation. See my report foran overview of the use of quaternions in this application.
// User must call 'AHRSupdate()' every sample period and parsecalibrated gyroscope ('gx', 'gy', 'gz'),
// accelerometer ('ax', 'ay', 'ay') and magnetometer ('mx', 'my', 'mz')data. Gyroscope units are
// radians/second, accelerometer and magnetometer units are irrelevantas the vector is normalised.
#include "AHRS.h"
#include <math.h>
#include <stdio.h>
/* Private define------------------------------------------------------------*/
#define Kp 2.0f // proportional gain governs rate of convergence toaccelerometer/magnetometer
#define Ki 0.005f // integral gain governs rate of convergenceof gyroscope biases
#define halfT 0.0025f // half the sample period
#define ACCEL_1G 1000 //theacceleration of gravity is: 1000 mg
/* Private variables---------------------------------------------------------*/
static float q0 = 1, q1 = 0, q2 = 0, q3 = 0; // quaternion elements representing theestimated orientation
static float exInt = 0, eyInt = 0, ezInt = 0; // scaled integral error
/* Public variables----------------------------------------------------------*/
EulerAngle_Type EulerAngle; //unit: radian
u8InitEulerAngle_Finished = 0;
float Magnetoresistor_mGauss_X = 0, Magnetoresistor_mGauss_Y = 0,Magnetoresistor_mGauss_Z = 0;//unit: milli-Gauss
float Accelerate_mg_X, Accelerate_mg_Y, Accelerate_mg_Z;//unit: mg
float AngularRate_dps_X, AngularRate_dps_Y, AngularRate_dps_Z;//unit:dps: degree per second
int16_t Magnetoresistor_X, Magnetoresistor_Y, Magnetoresistor_Z;
uint16_t Accelerate_X = 0, Accelerate_Y = 0, Accelerate_Z = 0;
uint16_t AngularRate_X = 0, AngularRate_Y = 0, AngularRate_Z = 0;
u8 Quaternion_Calibration_ok = 0;
/* Private macro-------------------------------------------------------------*/
/* Private typedef-----------------------------------------------------------*/
/* Private function prototypes -----------------------------------------------*/
//版权声明：本文为CSDN博主「_Summer__」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
//原文链接：https://blog.csdn.net/qq_21842557/article/details/50993809
//导航坐标系(参考坐标系)n，选取东北天右手直角坐标系作为导航坐标系n、载体坐标系(机体坐标系)b，
//选取右手直角坐标系定义：四轴向右为X正方向，向前为Y轴正方向，向上为Z轴正方向。
void AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz)
{
float norm;
float hx, hy, hz, bx, bz;
float vx, vy, vz, wx, wy, wz;
float ex, ey, ez;
// 定义一些辅助变量用于转换矩阵
float q0q0 = q0*q0;
float q0q1 = q0*q1;
float q0q2 = q0*q2;
float q0q3 = q0*q3;
float q1q1 = q1*q1;
float q1q2 = q1*q2;
float q1q3 = q1*q3;
float q2q2 = q2*q2;
float q2q3 = q2*q3;
float q3q3 = q3*q3;
// 归一化加速度计和地磁计的度数
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm;
ay = ay / norm;
az = az / norm;
norm = sqrt(mx*mx + my*my + mz*mz);
mx = mx / norm;
my = my / norm;
mz = mz / norm;
//将b系中的地磁计分量[mx,my,mz]转换到n系,得到[hx,hy,hz]
hx = 2*mx*(0.5 - q2q2 - q3q3) + 2*my*(q1q2 - q0q3) + 2*mz*(q1q3 + q0q2);
hy = 2*mx*(q1q2 + q0q3) + 2*my*(0.5 - q1q1 - q3q3) + 2*mz*(q2q3 - q0q1);
hz = 2*mx*(q1q3 - q0q2) + 2*my*(q2q3 + q0q1) + 2*mz*(0.5 - q1q1 - q2q2);
//得到n系中的地磁向量的真实值[bx,bz,by],其中by=0
bx = sqrt((hx*hx) + (hy*hy));
bz = hz;
//n系中的地磁向量[bx，by,bz]转换到b系中，得到[wx,wy,wz]
wx = 2*bx*(0.5 - q2q2 - q3q3) + 2*bz*(q1q3 - q0q2);
wy = 2*bx*(q1q2 - q0q3) + 2*bz*(q0q1 + q2q3);
wz = 2*bx*(q0q2 + q1q3) + 2*bz*(0.5 - q1q1 - q2q2);
//n系中重力加速度[0,0,1]转换到b系中得到三个分量[vx,vy,vz]
vx = 2*(q1q3 - q0q2);
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
//计算[wx,wy,wz] X [mx,my,mz],[ax,at,az] X [vx,vy,vz]，得到两个误差后求和
ex = (ay*vz - az*vy) + (my*wz - mz*wy);
ey = (az*vx - ax*vz) + (mz*wx - mx*wz);
ez = (ax*vy - ay*vx) + (mx*wy - my*wx);
//PI控制器中的积分部分
exInt = exInt + ex*Ki* (1.0f / sampleFreq);
eyInt = eyInt + ey*Ki* (1.0f / sampleFreq);
ezInt = ezInt + ez*Ki* (1.0f / sampleFreq);
//误差经过PI控制器后输出,然后补偿到角速度的三个分量，Kp、Ki是需要调节的参数
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
//一阶龙格库塔法更新四元数
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
// 归一化四元数
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
}
/axis is a unit vector
local_rotation.w = cosf( fAngle/2)
local_rotation.x = axis.x * sinf( fAngle/2 )
local_rotation.y = axis.y * sinf( fAngle/2 )
local_rotation.z = axis.z * sinf( fAngle/2 )
//代码是抄的，抄的时候忘记了加出处。
//大体意思是将 [0 0 g]的在地理坐标系下的重力向量旋转到载体坐标系上
//和载体坐标系上的加速度计进行叉乘，求出误差
// 相同的，磁力计也是一样旋转到载体坐标系上，求出误差
// 误差很小的情况下，sinx约等于x，相加进行进行误差补偿，加上PI控制
// 磁力计和[0 0 g]每种只能补偿两个轴，(加速度计和磁力计)(这里之后需要详细说下)，
// 比如说加速度计无法感知Z轴变化。四、实际测量使用
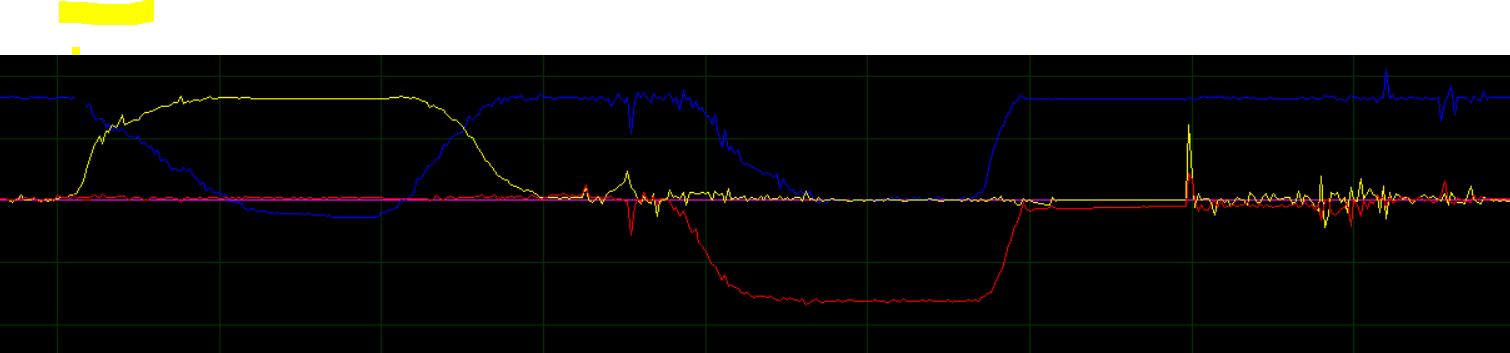
使用的小钢炮板子，juma，现在官网都没了，是个STM32F401，板载的外设很多，此处是用板载的LSM6DS3 ，貌似也是ST的，输出的加速度计的值，发现的确加速度计无法感知绕Z轴的变化，绕X轴和Y轴旋转，蓝色是Z轴分量，平铺的板子左边翘起放平以及前边翘起的波形图(采用的串口，模拟示波器，这个很早我就上传了，当时飞思卡尔时候就用着很好用)，当机体受力平衡的时候加速度计就是[0, 0, g]。
// UPDATE 20230507
// 有错误以及写的不好不对看不懂的地方及时沟通
// 如有原作有意见的及时沟通
