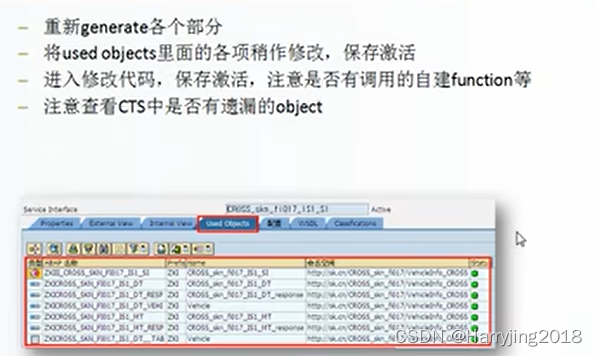
1.单选(2分)
已知一个有向图的邻接矩阵表示,要删除所有从第i个结点发出的边,操作为( )。
A.将邻接矩阵的第i列删除
B.将邻接矩阵的第i行元素全部置为0
C.将邻接矩阵的第i列元素全部置为0
D.将邻接矩阵的第i行删除
2.单选(2分)
假设有向图含n个顶点及e条弧,则表示该图的邻接表中包含的弧结点个数为( )。
A.e
B.2*e
C.n*e
D.n
3.单选(2分)
关键路径是事件结点网络中( )。
A.图中最长的回路
B.图中最短的回路
C.从源点到汇点的最短路径
D.从源点到汇点的最长路径
4.单选(2分)
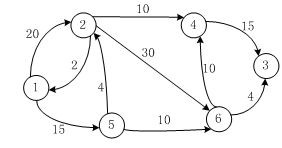
AOE网如下图所示,其关键路径( )。
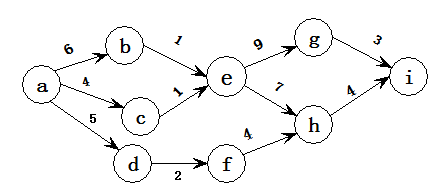
A.abehi
B.acegi
C.abegi
D.adfhi
5.单选(2分)
针对下图利用Dijkstra算法求从顶点1到其他点的最短路径,下面最短路径不正确的有( )。
A.1,5,6
B.1,5,2
C.1,2,4
D.1,5,6,3
6.单选(2分)
具有n个顶点的无向完全图,边的总数是( )。
A.n*(n+1)
B.n*n
C.n*(n-1)/2
D.n/2
7.单选(2分)
有n个顶点的强连通有向图G至少有( )条边。
A.n*(n-1)
B.n
C.n*(n-1)/2
D.n-1
8.单选(2分)
一个具有n个顶点的有向图中,若所有顶点的出度数之和为m,则所有顶点的度数之和是( )。
A.2*n
B.n
C.2*m
D.m
9.单选(2分)
非空无向图的邻接矩阵一定是( )。
A.对称矩阵
B.下三角矩阵
C.对角矩阵
D.零矩阵
10.单选(2分)
在含有n个顶点m条边的不带权无向图的邻接矩阵中,零元素的个数为( )。
A.n*n-2*m
B.2*m
C.n*n-m
D.m
11.单选(2分)
一个图的邻接表表示中有奇数个边节点,则该图一定是( )
A.有向图或无向图
B.无向图
C.有向图
D.完全图
12.单选(2分)
具有n个顶点的连通图中的任意一条简单路径,其长度不可能超过( )。
A.n
B.n/2
C.1
D.n-1
13.单选(2分)
图的深度优先遍历类似于树的( )遍历。
A.中序
B.后序
C.层序
D.先序
14.单选(2分)
对于n个顶点e条边的连通图,利用Prim算法求最小生成树的时间复杂度为( )。
A.O(n)
B.O(e)
C.O(nlogn)
D.O(n*n)
15.单选(2分)
对于n个顶点e条边的连通图,利用Kruskal算法求最小生成树的时间复杂度为( )。
A.O(nlogn)
B.O(eloge)
C.O(n)
D.O(n*n)
16.单选(2分)
图的广度优先遍历类似于树的( )遍历。
A.先序
B.层序
C.后序
D.中序
17.单选(2分)
一个有N个顶点和N条边的无向图一定是( )。
A.连通图
B.非连通图
C.完全图
D.强连通图
18.单选(2分)
一个有28条边的非连通无向图至少有( )个顶点。
A.8
B.9
C.7
D.6
19.单选(2分)
若无向图G =(V,E)中含7个顶点,要保证图G在任何情况下都是连通的,则需要的边数最少是( )。
A.6
B.21
C.16
D.15
20.单选(2分)
在有向图G的拓扑序列中,若顶点Vi在顶点Vj之前,则下列情形不可能出现的是( )。
A.G中有一条从Vj到Vi的路径
B.G中没有弧<Vi,Vj>
C.G中有一条从Vi到Vj的路径
D.G中有弧<Vi,Vj>
21.单选(2分)
下列关于AOE网的叙述中,不正确的是( )。
A.所有的关键活动提前完成,那么整个工程将会提前完成
B.某些关键活动提前完成,那么整个工程将会提前完成
C.任何一个关键活动提前完成,那么整个工程将会提前完成
D.关键活动不按期完成就会影响整个工程的完成时间
22.单选(2分)
下列说法不正确的是( )。
A.图的遍历是从给定的源点出发每一个顶点仅被访问一次
B.遍历的基本算法有两种:深度遍历和广度遍历
C.图的深度遍历是一个递归过程
D.图的深度遍历不适用于有向图
23.单选(2分)
判断有向图中是否存在回路,除了可以用拓扑排序外,还可以采用( )。
A.深度优先遍历算法
B.广度优先遍历算法
C.最短路径Dijkstra算法
D.求关键路径的方法
24.单选(2分)
任何一个无向连通图的最小生成树( )。
A.一定有多棵
B.只有一棵
C.有一棵或多棵
D.不存在
25.单选(2分)
用Prim算法和Kruskal算法构造图的最小生成树,所得到的最小生成树( )。
A.不相同
B.相同
C.可能相同,也可能不同
D.无法比较
26.单选(2分)
若一个有向图的所有顶点不能排在一个拓扑序列中,则可判定该有向图是( )。
A.含有多个入度为0的顶点
B.是一个强连通图
C.是一个有根的有向图
D.含有顶点数大于1的强连能分量
27.单选(2分)
在有N个顶点的有向图中,每个顶点的度最大可达多( )。
A.N
B.2*N
C.2*N-2
D.N-1
28.单选(2分)
具有12个顶点,36条边的有向图,所有顶点度的和为( )。
A.36
B.72
C.24
D.48
29.单选(2分)
在一个具有n个顶点和e条边的有向图的邻接矩阵中,表示边存在的元素个数为( )。
A.n
B.e
C.3*e
D.n*e
30.单选(2分)
在一个具有n个顶点和e条边的无向图的邻接矩阵中,表示边存在的元素(又称为有效元素)的个数为( )。
A.2*e
B.n*e
C.n
D.e