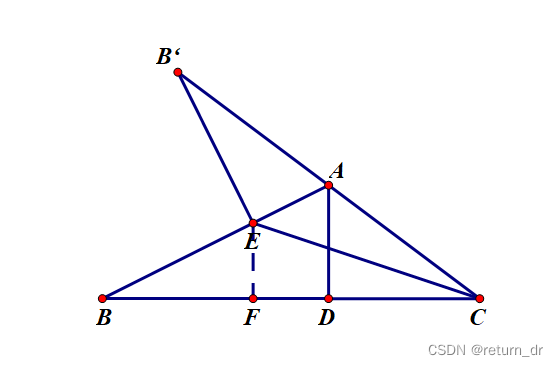
如图,在 △ A B C \triangle ABC △ABC 中, A C > 5 , A B > A C AC>5,AB>AC AC>5,AB>AC,点 E E E 是 A B AB AB 上一点,链接 C E CE CE,将 △ B C E \triangle BCE △BCE 沿 C E CE CE 折叠,点 B B B 的对应点 B ′ B' B′ 落在 C A CA CA 的延长线上,展开铺平,过点 A A A 作 A D ⊥ B C AD\perp BC AD⊥BC 于 D D D,若 A D = 3 , ∠ B E C = 13 5 ∘ AD=3,\angle BEC=135^\circ AD=3,∠BEC=135∘,求 B E BE BE 的长。
解:过点 E E E 作 E F ⊥ B C EF \perp BC EF⊥BC
又 ∵ A D ⊥ B C \because AD \perp BC ∵AD⊥BC
∴ ∠ B F E = ∠ C F E = ∠ A D C = 9 0 ∘ \therefore \angle BFE = \angle CFE = \angle ADC = 90^\circ ∴∠BFE=∠CFE=∠ADC=90∘
∵ \because ∵ 在 △ A C D \triangle ACD △ACD 中, ∠ A D C = 9 0 ∘ \angle ADC = 90^\circ ∠ADC=90∘, A D = 3 , A C = 4 AD = 3,AC = 4 AD=3,AC=4
∴ A C = A D 2 + C D 2 = 5 \therefore AC = \sqrt{AD^2 + CD^2} = 5 ∴AC=AD2+CD2=5
设 ∠ A C B = α \angle ACB = \alpha ∠ACB=α,则由折叠, ∠ B C E = 1 2 α \angle BCE = \dfrac{1}{2} \alpha ∠BCE=21α
∴ sin α = 3 5 , cos α = 4 5 \therefore \sin \alpha = \dfrac{3}{5},\cos \alpha = \dfrac{4}{5} ∴sinα=53,cosα=54
∴ sin 1 2 α = 1 − cos α 2 = 1 − 4 5 2 = 1 10 \therefore \sin \dfrac{1}{2} \alpha = \sqrt{\dfrac{1 - \cos \alpha}{2}} = \sqrt{\dfrac{1-\dfrac{4}{5}}{2}} = \dfrac{1}{\sqrt{10}} ∴sin21α=21−cosα=21−54=101
∴ E F E C = 1 10 \therefore \dfrac{EF}{EC} = \dfrac{1}{\sqrt{10}} ∴ECEF=101
∵ ∠ E F C = ∠ A D C = 9 0 ∘ \because \angle EFC = \angle ADC = 90^\circ ∵∠EFC=∠ADC=90∘
∴ E F ∥ A D \therefore EF \parallel AD ∴EF∥AD
∴ ∠ B A C = ∠ B E C = 13 5 ∘ , ∠ B E F = ∠ B A D \therefore \angle BAC = \angle BEC = 135^\circ, \angle BEF = \angle BAD ∴∠BAC=∠BEC=135∘,∠BEF=∠BAD
∴ ∠ B A D = 13 5 ∘ − ( 9 0 ∘ − α ) = 4 5 ∘ + α \therefore \angle BAD = 135^\circ - (90^\circ - \alpha) = 45^\circ + \alpha ∴∠BAD=135∘−(90∘−α)=45∘+α
∴ ∠ B E F = ∠ B A D = 4 5 ∘ + α \therefore \angle BEF = \angle BAD = 45^\circ + \alpha ∴∠BEF=∠BAD=45∘+α
∴ sin ∠ B E F = sin ( 4 5 ∘ + α ) = s i n 4 5 ∘ cos α + cos 4 5 ∘ sin α = 2 5 5 \therefore \sin \angle BEF = \sin(45^\circ + \alpha) = sin45^\circ \cos \alpha + \cos 45 ^\circ\sin \alpha = \dfrac{2\sqrt{5}}{5} ∴sin∠BEF=sin(45∘+α)=sin45∘cosα+cos45∘sinα=525
∴ B F B E = 2 5 5 ( 即 △ B E F 和 △ A B D 为 1 : 2 : 5 的三角形 ) \therefore \dfrac{BF}{BE} = \dfrac{2\sqrt{5}}{5}(即\triangle BEF和\triangle ABD为1:2:\sqrt{5}的三角形) ∴BEBF=525(即△BEF和△ABD为1:2:5的三角形)
∴ B D = 2 A D = 6 \therefore BD = 2AD = 6 ∴BD=2AD=6
设 E F = x , EF = x, EF=x, 则 B F = 2 x , C F = 3 x BF = 2x,CF = 3x BF=2x,CF=3x
∴ B F + C F = B C \therefore BF + CF = BC ∴BF+CF=BC
即 2 x + 3 x = 10 2x+3x=10 2x+3x=10 解得 x = 2 x=2 x=2
∴ B E = 5 B E = 2 5 \therefore BE = \sqrt{5} BE = 2\sqrt{5} ∴BE=5BE=25


![K8S管理系统项目实战[API开发]-2](https://img-blog.csdnimg.cn/27e2b8811f3645d5b5e29dcbc1715515.png)


![JavaWeb07(MVC应用01[家居商城]连接数据库)](https://img-blog.csdnimg.cn/6ae1e3e29d924f06b6dc6eb4e4570fee.png)