在这里的开头需要讲述一下碎片，碎片分为内碎片和外碎片两种。

内碎片：分区之内未被利用的空间
外碎片：分区之间难以利用的空闲分区（通常是小空闲分区）。

连续分配存储管理方式:

为了能将用户程序装入内存，必须为它分配一定大小的内存空间。

1.单一连续分配

只能在单道程序环境下，整个内存的用户空间由单个程序独占。

剩余分配方式详见操作系统——内存分配与回收_操作系统内存回收_用编程写诗的博客-CSDN博客

2.固定分区分配

分区个数固定，分区大小固定。注意大小固定并不是大小相等！！！

将内存用户空间划分为若干个固定大小的区域，在每个分区中只装入一道作业。

划定分区的方法为：分区固定和分区不固定

一般会产生一个分区分配表如图所示：

固定分区的优点：它是最早出现的分区方法这个方法思路以及实现很简单，很容易实现。

固定分区的缺点：由于它的大小是固定的所以必然出现空间的浪费会产生很多内碎片。

3.动态分区分配

动态分区分配又称为可变分区分配。从名字中就可以看出来，它和固定分区分配所不同的就是它在分配内存分区的时候是动态的。它虽然解决了内碎片的问题但是会带来外碎片的问题。

它会产生一个空闲分区表区别于固定分区分配的分区说明表。如下表所示：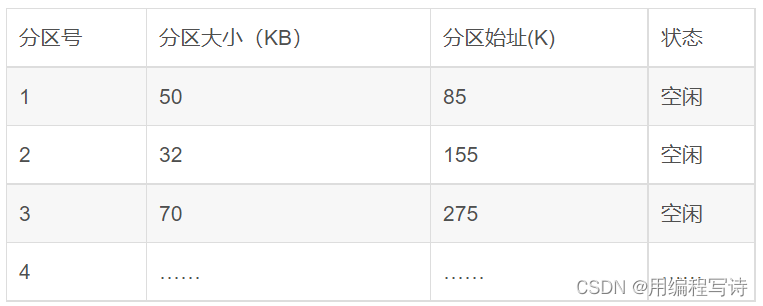

 动态分区的大小的不确定的那么它进行分配的时候就不是单独的进行寻找大小找到大小接近的分区那么简单了。需要考虑到动态分区分配算法了。这里提出三种顺序搜索的算法：

1.首次适应算法：

从首地址开始顺序查找，直到找到一个大小能满足要求的空闲分区为止。

该算法的优势：

1.就是优先利用了内存中低地址的部分的空闲分区，从而保留了高地址部分的大空闲。

但是它的缺点也很明显：

1.低地址部分被不断划分，导致留下了许多的难以利用的，很小的空闲分区也就是碎片。

2.每次查找都是从低地址开始查找由于低地址都先被占用了所以只能往后面找无疑是增大了很多开销。

2.最佳适应算法：

指的是每次在分配的时候总是把能满足要求的，又是最小的空闲分区分配避免大材小用。该算法要求所有的空闲分区按照从小到大的顺序排列来提高寻找的速度。直接查找到最佳的位置。

该算法的优势：

1.就是第一次能找到的空闲分区肯定是最好的最合适的，从孤立来看该算法是最佳的。

但是它的缺点也很明显：

1.首先他需要从小到大进行排序并进行查找位置所以会增加很多开销尤其是对于计算机种成千上万的空闲位置。

2.其次它虽然是找到了最佳的位置但是在划分之后产生的空闲空间必然是最小的。例如需要占用8K内存系统分配了9K孤立来看肯定是最佳的但是产生的1K的空间很大概率无法再使用所以会产生很多碎片导致浪费。

3.最坏适应算法：

最坏适应算法和最佳适应算法是相反的，它是要求系统分配一个最大的空闲分区进行分配。它要求空闲分区按照从大到小的顺序进行排序。查找时候只需要看第一个是否满足分配即可。

该算法的优势：

1.由于最开始分配的空间是最大的，所以分配后剩下的空间不至于太小，所以产生的碎片不会太多不会产生碎片问题。

2.它在分配的时候进行查找空闲分区表的时候只需要看第一个大小是否满足即可所以效率很快。

但是它的缺点也很明显：

1.由于总是把最大的分区进行划分所以到最后系统中没有大的分区导致后面的大的进程无法分配相对应大小的空间。

上面讲述的基于顺序的查找算法，下面介绍基于索引的查找算法。这个主要掌握它的基本思想。

1.快速适应算法：这个是将空闲分区根据大小进行分类，对于每一类具有相同容量的所有空闲分区，单独设立一个空闲分区链表。该算法仅需要根据进程的长度，寻找到能容纳它的最小空闲区链表，并取下第一块进行分配即可。在分配过程中，不会对任何分区产生分割。

2.伙伴系统：这个是无论已分配分区还是空闲分区它的大小都是2的K次幂

当需要为进程分配一个长度为 n 的存储空间时，首先计算一个 i 值，使 2^(i-1) < n ≤ 2^i，然后在空闲分区大小为 2^i 的空闲分区链表中查找。若找到则直接分配。否则，则在分区大小为 2^(i+1) 的空闲分区链表中寻找。若存在 2^(i+1) 的一个空闲分区，则把该空闲分区分为相等的两个分区，这两个分区称为一对伙伴，其中的一个分区用于分配，而把另一个加入分区大小为 2^i 的空闲分区链表中。若仍然找不到，依次类推去寻找更高1次幂的分区。
与一次分配可能要进行多次分割一样，一次回收也可能要进行多次合并，如回收大小为 2^i的空闲分区时，若事先已存在回收块所对应的2^i伙伴块的空闲分区时，则应将其与伙伴分区合并为大小为2^(i+1)的空闲分区，若事先已存在新合并空闲块对应的2^(i+1)伙伴块的空闲分区时，依次类推合并。

3.哈希算法：构造一张以空闲分区大小为关键字的哈希表，该表的每一个表项记录了一个对应的空闲分区链表表头指针。

关于内存的回收问题：

关于内存的回收，总共可以有四种情况：

1.回收区上面的分区是空闲分区

2.回收区下面的分区是空闲分区

3.回收区上面下面的分区都是空闲分区

4.回收区上面下面的分区都不是空闲分区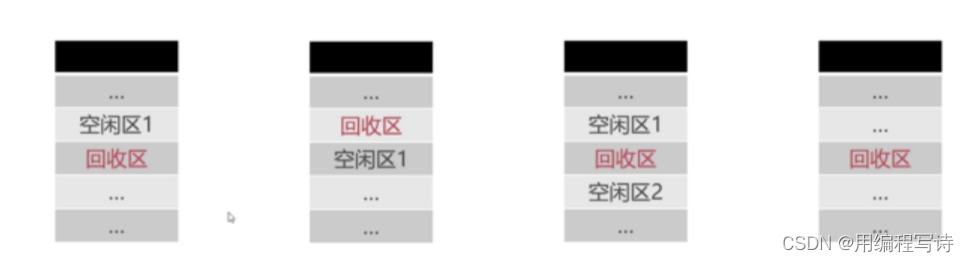

每种情况的回收情况

1.回收区在空闲区下面：

使用空闲链表的数据结构来保存空闲区，不需要新建空闲链表节点、只需要将空闲区的容量增大为原来空闲区和回收区的容量之和即可(也就是将回收区包含进来)

2.回收区在空闲区上面：

将回收区与空闲区合并的容量大小为新的空闲区的容量大小，新的空闲区在空闲链表中的地址使用之前回收区的地址

3.回收区在两个空闲区中间：

将两个回收区与空闲区合并的容量大小为新的空闲区的容量大小，新的空闲区在空闲链表中的地址使用之前空闲区1的地址

4.单独的回收区：

新建一个单独的地址节点放到空闲链表当中，大小为回收区的大小。