系列文章
- 双目视觉(一)双目视觉系统
- 双目视觉(二)双目匹配的困难和评判标准
- 双目视觉(三)立体匹配算法
- 双目视觉(四)匹配代价
- 双目视觉(五)立体匹配算法之动态规划全局匹配
- 双目视觉(六)U-V视差
- 【项目实战】利用U-V视差进行地面检测
- 【项目实践】U-V视差路面检测之动态规划
这里介绍ORB_SLAM算法中的双目匹配算法
双目匹配
在ORB_SLAM采用粗匹配和精匹配结合的方式来实现双目特征点的精确匹配
1.粗匹配
假设双目相机已被标定好,即双目相机的左右图像的极线相互平行,那么理论上左右图像中共轭点的坐标仅在u轴上不同
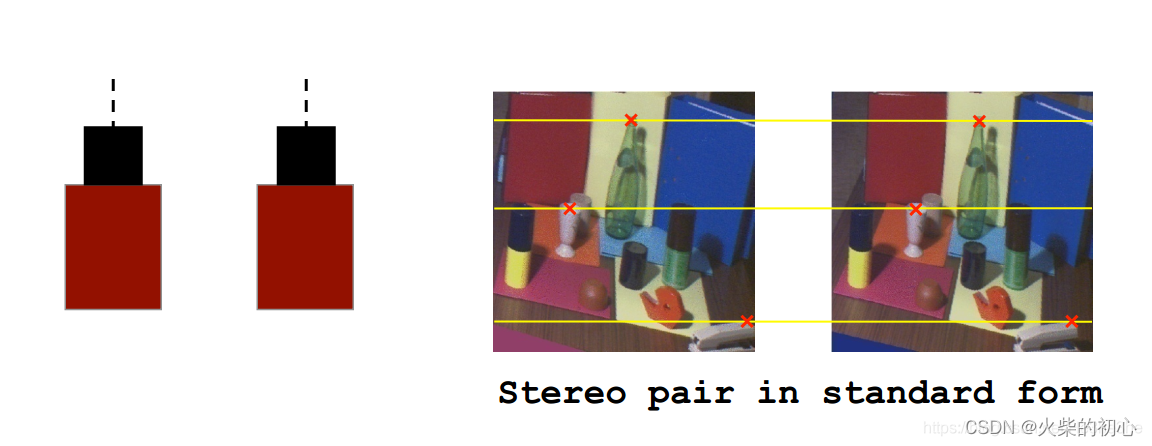
为了寻找左图中的某一特征点在右图中对应的匹配点, 可以通过沿该特征点对应的极线进行搜索,这样避免了在整幅右图像上进行搜索,同时提高了匹配的速度。
然而, 由于误差的影响, 匹配点对的坐标在v方向可能存在几个像素的偏差,这样会造成沿极线搜索时无法匹配到最佳的特征点。因此,为了减少误差的影响,沿极线在v方向扩展一定的范围形成一个带状区域,将右图中待匹配的特征点按y 坐标分配到相应的带状区域
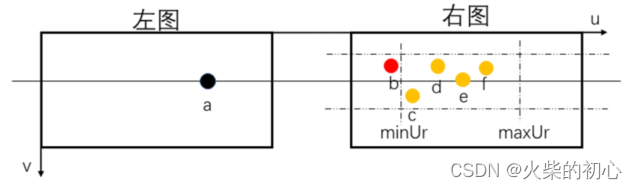
选取左图像中的某一特征点,如a,与对应的带状区域内中的点,如b, c, d, e, f,逐一进行描述子的比较,寻找最佳的匹配点。其中,待匹配集合中的特征点的x坐标理论上应该落在
[
m
i
n
U
r
,
m
a
x
U
r
]
\left[minU_{r}, maxU_{r}\right]
[minUr,maxUr]范围内,而
[
m
i
n
U
r
,
m
a
x
U
r
]
\left[minU_{r}, maxU_{r}\right]
[minUr,maxUr]可以通过公式确 定。 因 此, 可以预先 筛选掉落在
[
m
i
n
U
r
,
m
a
x
U
r
]
\left[minU_{r}, maxU_{r}\right]
[minUr,maxUr]之外的点b。
{
max
d
=
f
⋅
B
min
Z
min
d
=
f
⋅
B
max
Z
⇒
{
max
U
r
=
U
l
−
min
d
min
U
r
=
U
l
−
max
d
\left\{\begin{array} { l } { \operatorname { max } d = \frac { f \cdot B } { \operatorname { m i n } Z } } \\ { \operatorname { min } d = \frac { f \cdot B } { \operatorname { m a x } Z } } \end{array} \Rightarrow \left\{\begin{array}{l} \max U_{r}=U_{l}-\min d \\ \min U_{r}=U_{l}-\max d \end{array}\right.\right.
{maxd=minZf⋅Bmind=maxZf⋅B⇒{maxUr=Ul−mindminUr=Ul−maxd
2.精匹配
在经过了粗匹配后, 左图像中的特征点在右图像中对应的带状区域内寻找到了最佳的匹配点,但是由于特征点的坐标可能不是那么精准,此时的匹配点可能并不是真正的最佳匹配点, 因此需要在粗匹配的基础上进一步进行精匹配。 通过在当前匹配点的位置附近构建滑动窗口,然后使用模板匹配算法寻找更优的位置
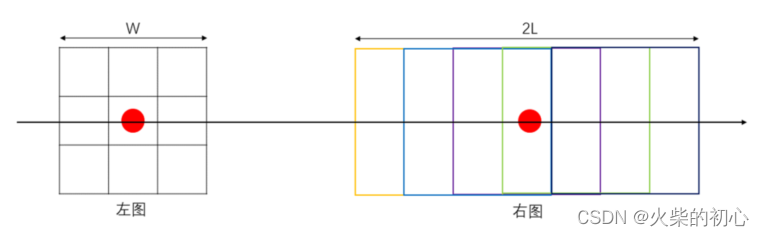
左右红点是双目图像通过粗匹配后得到的匹配点对,以左图的匹配点为中心取一个宽为W的图像块,然后在右图中构建一个相同尺寸的图像块, 在搜索范围
[
−
L
,
L
]
\left[-L, L\right]
[−L,L]内从左向右滑动窗口, 并通过模板匹配算法依次计算两个图像块的相似度, 最终找到最佳的匹配位置, 其中相似度计算:
S
A
D
(
u
,
v
,
l
)
=
∑
i
=
−
w
2
w
2
∑
j
=
−
w
2
w
2
∣
I
l
(
u
+
i
,
v
+
j
)
−
I
r
(
u
+
i
+
l
,
v
+
j
)
∣
,
l
∈
(
−
L
,
L
)
S A D(u, v, l)=\sum_{i=-\frac{w}{2}}^{\frac{w}{2}} \sum_{j=-\frac{w}{2}}^{\frac{w}{2}}\left|I_{l}(u+i, v+j)-I_{r}(u+i+l, v+j)\right|, l \in(-L, L)
SAD(u,v,l)=i=−2w∑2wj=−2w∑2w∣Il(u+i,v+j)−Ir(u+i+l,v+j)∣,l∈(−L,L)