均摊时间复杂度，它对应的分析方法，摊还分析（或者叫平摊分析）

均摊时间复杂度应用的场景比它更加特殊、更加有限

 // array表示一个长度为n的数组
 // 代码中的array.length就等于n
 int[] array = new int[n];
 int count = 0;
 
 void insert(int val) {
    if (count == array.length) {
       int sum = 0;
       for (int i = 0; i < array.length; ++i) {
          sum = sum + array[i];
       }
       array[0] = sum;
       count = 1;
    }

    array[count] = val;
    ++count;
 }

这段代码实现了一个往数组中插入数据的功能。当数组满了之后，也就是代码中的 count == array.length 时，我们用 for 循环遍历数组求和，并清空数组，将求和之后的 sum 值放到数组的第一个位置，然后再将新的数据插入。但如果数组一开始就有空闲空间，则直接将数据插入数组。

先分析上述代码的时间复杂度

最理想的情况下，数组中有空闲空间，我们只需要将数据插入到数组下标为 count 的位置就可以了，所以最好情况时间复杂度为 O(1)。最坏的情况下，数组中没有空闲空间了，我们需要先做一次数组的遍历求和，然后再将数据插入，所以最坏情况时间复杂度为 O(n)。

平均时间复杂度是多少呢？答案是 O(1)

假设数组的长度是 n，根据数据插入的位置的不同，我们可以分为 n 种情况，每种情况的时间复杂度是 O(1)。除此之外，还有一种“额外”的情况，就是在数组没有空闲空间时插入一个数据，这个时候的时间复杂度是 O(n)。而且，这 n+1 种情况发生的概率一样，都是 1/(n+1)。所以，根据加权平均的计算方法，我们求得的平均时间复杂度就是：

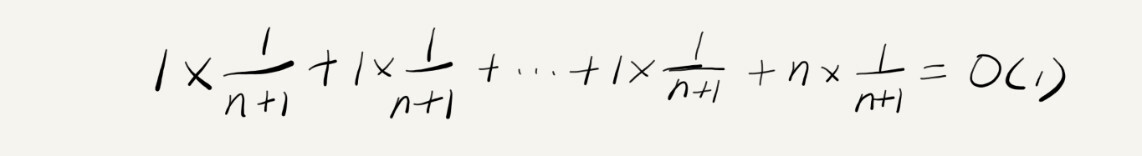
上述的分析过于复杂

可以使用摊还分析法，通过摊还分析得到的时间复杂度我们起了一个名字，叫均摊时间复杂度。

每一次 O(n) 的插入操作，都会跟着 n-1 次 O(1) 的插入操作，所以把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上，均摊下来，这一组连续的操作的均摊时间复杂度就是 O(1)。这就是均摊分析的大致思路。

听起来很复杂，但是均摊时间复杂度就是一种特殊的平均时间复杂度，我们没必要花太多精力去区分它们。你最应该掌握的是它的分析方法，摊还分析。至于分析出来的结果是叫平均还是叫均摊，这只是个说法，并不重要。

此文章为5月Day6学习笔记，内容来源于极客时间《数据结构与算法之美》