线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中的数据元素我们称之为顶点(Vertex)。
线性表中可以没有数据元素,称之为空表。树中可以没有结点,叫做空树。但图没有空图。
线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以为空。
无向边:若顶点vi到vj之间的边没有方向,则称这条边为五向边(Edge),用无序偶对(vi,vj)来表示。如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。
有向边:若从顶点vi到vj的边有方向,则称这条边为有向边 ,也称为弧(Arc),用有序偶<vi,vj>来表示,vi称为弧尾(Tail),vj称为弧头(Head)。顶点之间的边都是有向边,则称该图为有向图。
在图中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。
图有两种存储方式:
邻接矩阵:(二维数组)一维数组存顶点信息,二维数组存边的信息
无向图连接矩阵一定对称、有向图不一定对称
邻接表:(链表)
邻接矩阵实现图的插入和删除
# define SIZE 10 class Graph { public: Graph(); ~Graph(); void InsertVertex(char v); void InsertEdge(char v1, char v2); void PrintGraph(); int GetVertexInder(char v); void deleteEdge(char v1,char v2); void delVertex(char v); private: int m_MaxVertex; int m_NumVertex; int m_NumEdge; char* m_VertexArr; int m_Edge[SIZE][SIZE]; }; Graph::Graph() { m_MaxVertex = SIZE; m_NumVertex = m_NumEdge = 0; for (int i = 0; i < m_MaxVertex; ++i) { for (int j = 0; j < m_MaxVertex; ++j) { m_Edge[i][j] = 0; } } m_VertexArr = new char[m_MaxVertex]; } Graph::~Graph() { if (m_VertexArr != nullptr) { delete[]m_VertexArr; m_VertexArr = nullptr; } m_NumEdge = m_NumVertex = 0; } void Graph::InsertVertex(char v)//插入顶点 { if (m_NumVertex >= m_MaxVertex) { return; } m_VertexArr[m_NumVertex++] = v; } int Graph::GetVertexInder(char v) { for (int i = 0; i < m_NumVertex; i++) { if (v == m_VertexArr[i]) { return i; } } return -1; } void Graph::InsertEdge(char v1, char v2) { int p1 = GetVertexInder(v1); int p2 = GetVertexInder(v2); if (p1 == -1 || p2 == -1) { return; } m_Edge[p1][p2] = m_Edge[p2][p1] = 1; m_NumEdge++; } void Graph::PrintGraph() { int i, j; for (i = 0; i < m_NumVertex; i++) { cout << " "<<m_VertexArr[i] << " "; } cout << endl; for (i = 0; i < m_NumVertex; ++i) { cout << m_VertexArr[i] << " "; for (j = 0; j < m_NumVertex; ++j) { cout << m_Edge[i][j] << " "; } cout << endl; } } void Graph::deleteEdge(char v1, char v2) { int p1 = GetVertexInder(v1); int p2 = GetVertexInder(v2); if (p1 == -1 || p2 == -1) { return; } m_Edge[p1][p2] = m_Edge[p2][p1] = 0; m_NumEdge--; } void Graph::delVertex(char v) { //第一种删除方法,删除C。将C所在行和例后面的行和列依次前移 //int p1 = GetVertexInder(v); //if (p1 == -1) // return; //int delEdge = 0; //int i,j; //for (i = 0; i < m_NumVertex; ++i) //{ // if (m_Edge[p1][i] == 1) // { // delEdge++; // } //} //for (i = p1; i < m_NumVertex-1; ++i) //{ // m_VertexArr[i] = m_VertexArr[i + 1]; //} //for (i = p1; i < m_NumVertex-1; ++i) //{ // for (j = 0; j < m_NumVertex; ++j) // { // m_Edge[j][i] = m_Edge[j][i + 1];//移动列 // } //} //for (i = p1; i < m_NumVertex - 1; ++i) //{ // for (j = 0; j < m_NumVertex - 1; j++) // { // m_Edge[i][j] = m_Edge[i + 1][j];//移动行 // } //} //m_NumEdge = m_NumEdge - delEdge; //m_NumVertex--; //第二种删除方法:替换法,删除哪一行或列用最后一行或列对它进行替换。 int p1 = GetVertexInder(v); if (p1 == -1) return; int delEdge = 0; int i,j; for (i = 0; i < m_NumVertex; ++i) { if (m_Edge[p1][i] == 1) { delEdge++; } } m_VertexArr[p1] = m_VertexArr[m_NumVertex - 1]; for (i = 0; i < m_NumVertex; i++) { m_Edge[i][p1] = m_Edge[i][m_NumVertex - 1]; } for (i = 0; i < m_NumVertex - 1; i++) { m_Edge[p1][i] = m_Edge[m_NumVertex - 1][i]; } m_NumEdge = m_NumEdge - delEdge; m_NumVertex--; } void main() { Graph g; g.InsertVertex('A'); g.InsertVertex('B'); g.InsertVertex('C'); g.InsertVertex('D'); g.InsertEdge('A', 'B'); g.InsertEdge('A', 'D'); g.InsertEdge('B', 'C'); g.InsertEdge('B', 'D'); g.InsertEdge('C', 'D'); g.PrintGraph(); g.deleteEdge('A', 'B'); g.PrintGraph(); g.delVertex('C'); g.PrintGraph(); }运行结果:
邻接表:
/*邻接表*/ #define SIZE 10 class Edge//边 { public: Edge():m_next(nullptr){} Edge(char v):m_destindex(v) ,m_next(nullptr) {} int m_destindex;//邻接顶点的下标 Edge* m_next;//下一个邻接顶点的结点的地址 }; class vertex//顶点 { public: vertex():m_list(nullptr){} vertex(char v) :m_VerValue(v), m_list(nullptr){} int m_VerValue;//顶点的值 Edge* m_list;//之相邻顶点的链表 }; class GraphLink//图 { public: GraphLink(); ~GraphLink(); void InsertVertex(char v); void InsertEdge(char v1, char v2); void PrintGraph(); void DelVertex(char v); void DelEdge(char v1, char v2); int GetVertexIndex(char v); private: int m_MaxVertex; int m_NumVertex; int m_NumEdge; vertex* m_VerArr; }; GraphLink::GraphLink()//构造函数 { m_MaxVertex = SIZE;//最大顶点数 m_NumVertex = m_NumEdge = 0;//实际顶点数 m_VerArr = new vertex [m_MaxVertex];//new一个m_verArr数组 } GraphLink::~GraphLink()//析构函数 { if (m_VerArr != nullptr) { delete[]m_VerArr; m_VerArr = nullptr; } } void GraphLink::InsertVertex(char v) { if (m_NumVertex >= m_MaxVertex) return; m_VerArr[m_NumVertex++].m_VerValue = v;//m_NumVertexshiji顶点数,可以充当数组下标 } void GraphLink::InsertEdge(char v1, char v2) { int p1 = GetVertexIndex(v1); int p2 = GetVertexIndex(v2); if (p1 == -1 || p2 == -1) { return; } //V1->V2 即是在V1的边链表中插入值为p2的边节点 Edge* edge = new Edge(p2); edge->m_next = m_VerArr[p1].m_list; m_VerArr[p1].m_list = edge; edge = new Edge(p1); edge->m_next = m_VerArr[p2].m_list; m_VerArr[p2].m_list = edge; m_NumEdge++; } int GraphLink::GetVertexIndex(char v) { for (int i = 0; i < m_NumVertex; i++) { if (v == m_VerArr[i].m_VerValue) { return i; } } return -1; } void GraphLink::DelEdge(char v1, char v2) { int p1 = GetVertexIndex(v1); int p2 = GetVertexIndex(v2); if (p1 == -1 || p2 == -1) { return; } Edge* pf = nullptr; Edge* p = m_VerArr[p1].m_list; while (p != nullptr && p->m_destindex != p2) { pf = p; p = p->m_next; } if (p == nullptr)//v1到v2没有边 { return; } if (pf == nullptr)//if(p==m_verArr[p1].m_list) { m_VerArr[p1].m_list = p->m_next; } else { pf->m_next = p->m_next; } delete p; pf = nullptr; p = m_VerArr[p2].m_list; while (p->m_destindex != p1) { pf = p; p = p->m_next; } if (pf == nullptr) { m_VerArr[p2].m_list = p->m_next; } else { pf->m_next = p->m_next; } delete p; p = nullptr; m_NumEdge--; } void GraphLink::DelVertex(char v) { int pindex = GetVertexIndex(v); if (pindex == -1) { return; } Edge* p = m_VerArr[pindex].m_list; char destvalue; while (p != nullptr) { destvalue = m_VerArr[p->m_destindex].m_VerValue;//获得邻接顶点 DelEdge(v, destvalue); p = m_VerArr[pindex].m_list; } //覆盖 m_NumVertex--; m_VerArr[pindex].m_VerValue = m_VerArr[m_NumVertex].m_VerValue; m_VerArr[pindex].m_list = m_VerArr[m_NumVertex].m_list; //修改 Edge* q = nullptr; p = m_VerArr[pindex].m_list; while (p != nullptr) { int k = p->m_destindex; q = m_VerArr[k].m_list;//找到相关联的顶点的边链表 while (q) { if (q->m_destindex == m_NumVertex) { q->m_destindex = pindex; break; } q = q->m_next; } p = p->m_next; } } void GraphLink::PrintGraph() { Edge* p = nullptr; for (int i = 0; i < m_NumVertex; i++) { cout << i << " " << (char)m_VerArr[i].m_VerValue << ":"; p = m_VerArr[i].m_list; while (p) { cout << p->m_destindex << "->"; p = p->m_next; } cout << "nul" << endl; } } void main() { GraphLink lg; lg.InsertVertex('A'); lg.InsertVertex('B'); lg.InsertVertex('C'); lg.InsertVertex('D'); lg.InsertEdge('A', 'B'); lg.InsertEdge('A', 'C'); lg.InsertEdge('A', 'D'); lg.InsertEdge('B', 'C'); lg.InsertEdge('C', 'D'); lg.PrintGraph(); cout << "DelEdge" << endl; lg.DelEdge('A', 'D'); lg.PrintGraph(); cout << "DelGraph" << endl; lg.DelVertex('A'); lg.PrintGraph(); }运行结果:
数据结构:图的插入和删除
news2026/2/11 11:21:12
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/496949.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
2023年好用的MacBook文件管理软件推荐
我们已经有多年的 macOS 编程经验,也开发了很多大家都可以使用的工具。 我们可以解决各种 Mac 问题。 CleanMyMac X
这里是一些小建议:下载 CleanMyMac 即可快速解决本文章中提到的一些问题。但是,为了帮助您自行操作,我们还整理…
举一反三,从“温度转换“到“python蟒蛇绘制“,快速掌握Python语法
1.温度转换实例
我们先用Pychar写一个小程序,从这个小程序出发,我们将快速学习到python中的基础语法.本章中涉及到的语法只是初始语法部分,后续章节将会详细讲解python语法. "温度转换"实例编写:将两种温度体系转换.摄氏度转换为华氏度华氏度转换为摄氏度. 设计算法…
前端项目的通用优化策略
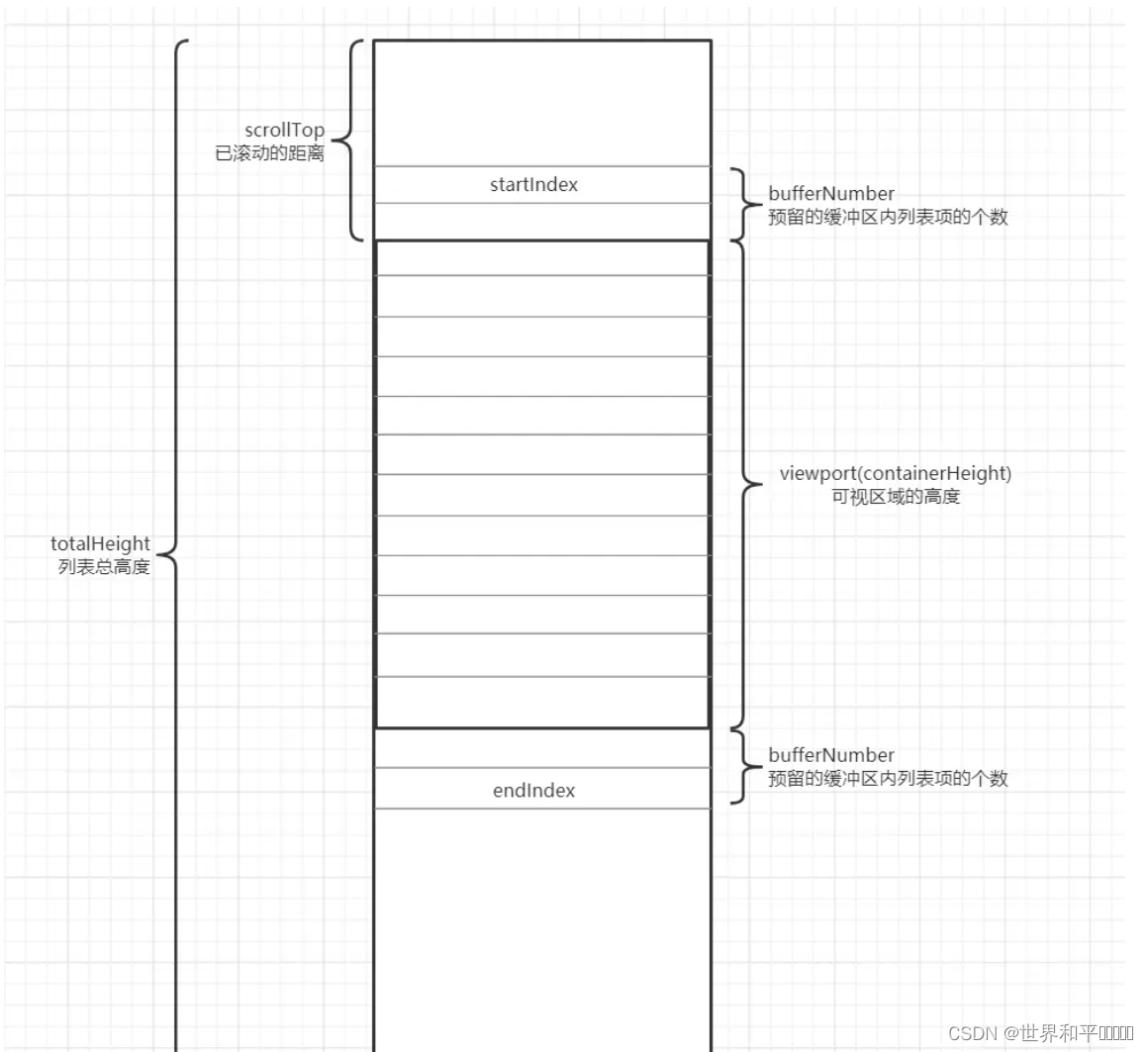
一、虚拟滚动
当我们开发的时候,遇到大数据加载,页面卡顿的问题应该如何处理?大多数情况下,我们都是尽量通过分页的方式处理这类问题,但是总有一些特殊的情况我们必须把数据全部加载到前端进行处理。我曾经遇到过一个…
智能优化算法:基于厨师的优化算法-附代码
智能优化算法:基于厨师的优化算法 文章目录 智能优化算法:基于厨师的优化算法1.基于厨师的优化算法1.1 初始化1.2 阶段1:厨师导师小组更新( X S 1 XS_1 XS1到 X S N c XS_{Nc} XSNc更新)1.3 阶段2:厨师…
Arduino处理json较大数据流以及GZIP数据流方法
Arduino处理json较大数据流以及GZIP数据流方法 ✨在一些需要使用网络并从网络数据平台获取数据的项目中,大多数据平台,提供支持的数据流格式,一般以json数据格式返回为主。 📓Arduino json数据流格式化处理方法 🏳🌈一般处理json数据基于都是通过ArduinoJson库来处理…
文本的清洗和标准化:如何处理混乱的数据?
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…
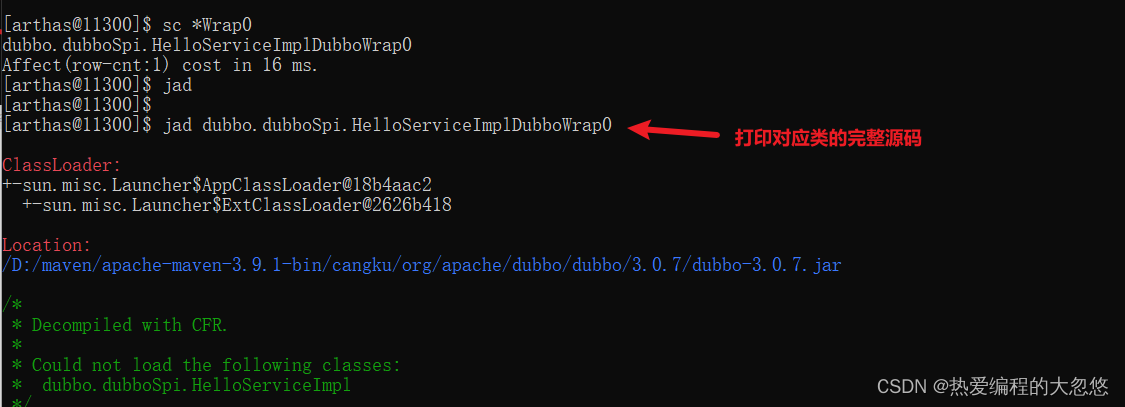
Dubbo源码篇02---从泛化调用探究Wrapper机制的原理
Dubbo源码篇02---从泛化调用探究Wrapper机制的原理 什么是泛化调用从传统三层架构说起反射调用尝试优化 泛化调用泛化调用怎么用通过Spring使用泛化调用 利用泛化调用改造现有服务 泛化调用小结 Wrapper机制自定义代理dubbo底层wrapper原理小结 小结 什么是泛化调用
从传统三层…
java实现大气污染排放传输路径模拟(iClientOpenlayer前端渲染)
开头先看下模拟实现效果图 一、技术应用及背景说明 了解大气污染传输路径模拟可以帮助我们更好地了解空气污染的来源和传播方式,从而采取更有效的控制措施。这种模拟技术可以根据大气环境和气象条件,模拟出污染物在大气中的传播路径和影响范围࿰…
树的储存结构和表示法_20230506
树的储存结构和表示法
前言
树是一类非常重要的数据结构,它是图和其它更高阶数据的基础,人们对树的储存结构和表示法进行了大量研究,这里介绍三种常见的链表结构来表示树的基本方法。
树的双亲表示法
假设以一组连续空间储存数据的结点&a…
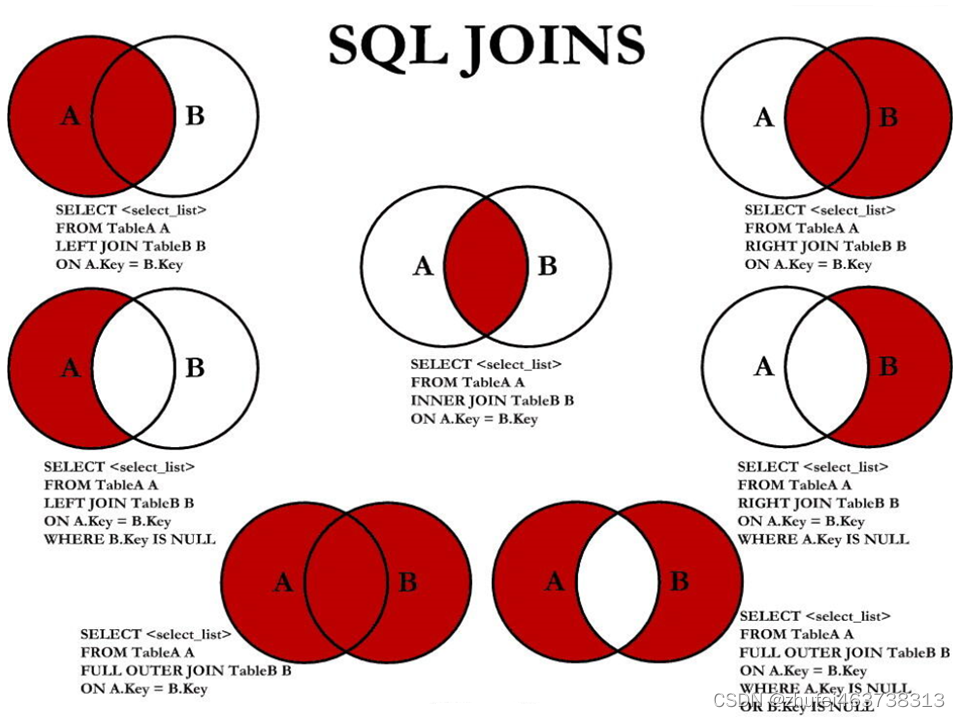
MySQL基础(六)多表查询
多表查询,也称为关联查询,指两个或更多个表一起完成查询操作。
前提条件:这些一起查询的表之间是有关系的(一对一、一对多),它们之间一定是有关联字段,这个关联字段可能建立了外键,…
密码学【java】初探究加密方式之非对称加密
文章目录 非对称加密1 常见算法2 生成公钥和私钥3 私钥加密4 私钥加密 公钥解密5 公钥和私钥的保存和读取5.1 **保存公钥和私钥**5.2 读取公钥和私钥 非对称加密
非对称加密算法又称现代加密算法。非对称加密是计算机通信安全的基石,保证了加密数据不会被破解。与对…
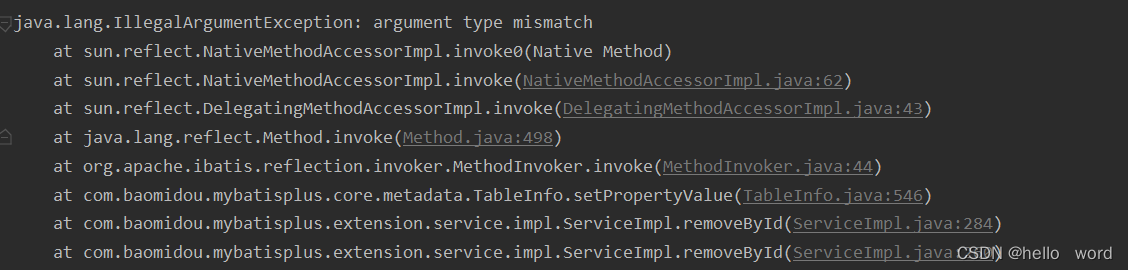
argument type mismatch
后端接收前端传来的数据 id,进行批量删除,报错如下:
错误一
removeByIds(ids) com.baomidou.mybatisplus.core.exceptions.MybatisPlusException: java.lang.IllegalArgumentException: argument type mismatch at com.baomidou.mybati…
华为OD机试 - 各位相加(Java)
一、题目描述
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。
二、思路与算法
各位相加,使用递归,出口是结果的长度等于1。
三、Java算法源码
public static int addDigits(int num) {recursion(num);re…
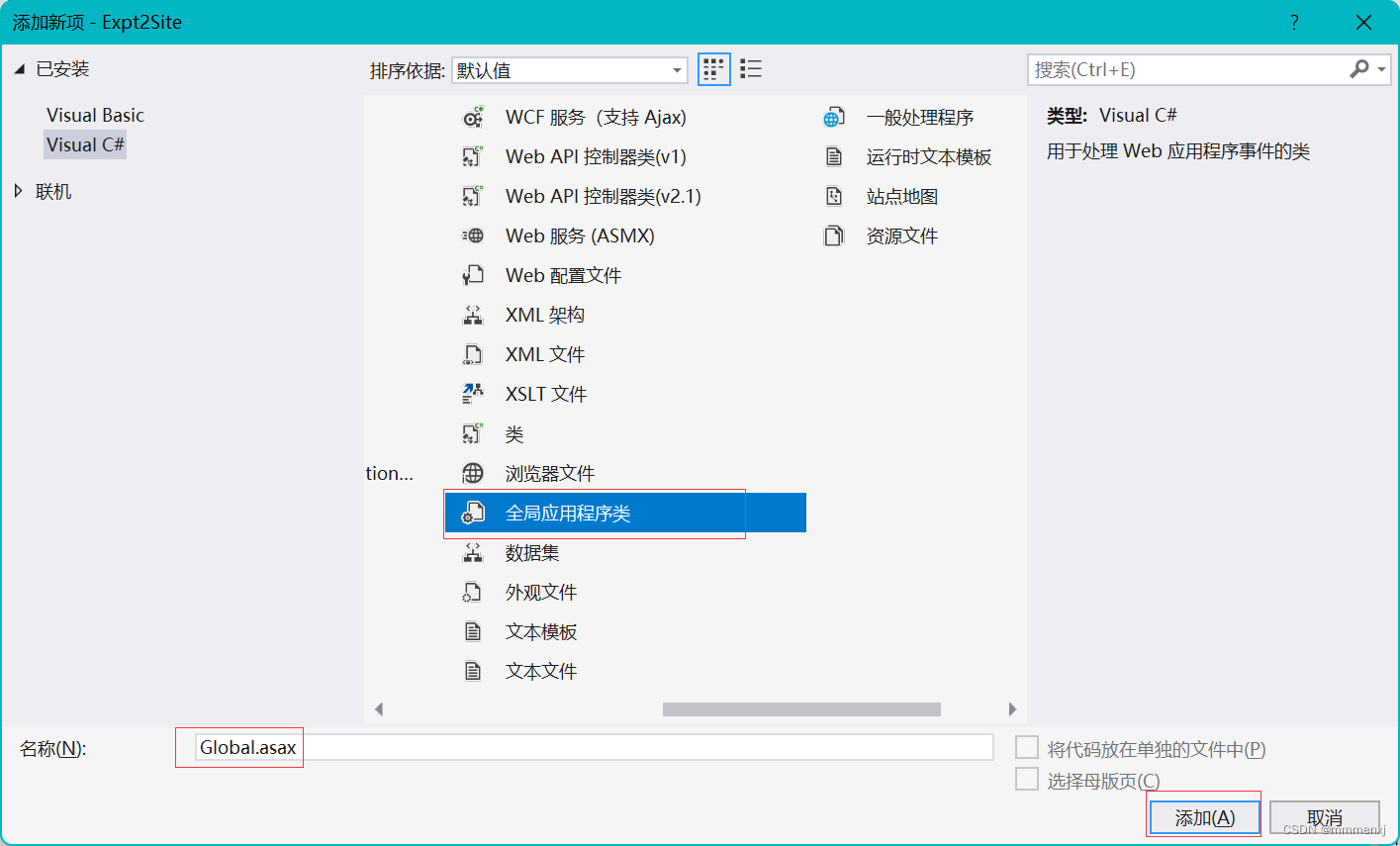
vs2017如何创建一个asax文件
VS2017无法为网站创建Global.asax文件,导致出现错误WebForms UnobtrusiveValidationMode 需要“jquery”ScriptResourceMapping。
解决方案如下: 勾选要应用的网站,这里我要应用的是ExSite
点击安装,然后点击确定即可。 此时&am…
单片机+PHY芯片+Powerlink协议实现高效数据采集探究(工业总线485和CAN的升级)
CAN总线和RS-485总线作为常用的工业通信总线,在许多工业领域中得到广泛使用。但随着工业应用的不断扩展和网络化的需求增加,它们面临着一些局限性。例如CAN总线虽然具有较高的通信速率和可靠性,但存在节点数量受限、数据传输距离短等问题。而…
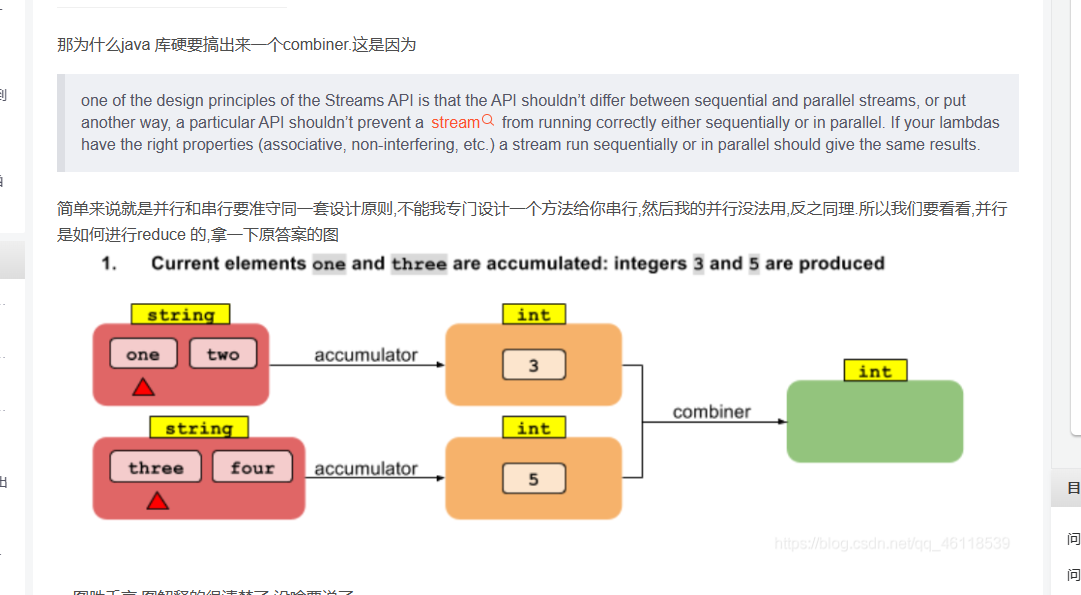
stream的collectors
起因的话,新进公司,看见了一段有意思的代码。
public final class MyCollectors {private MyCollectors() {}static final Set<Collector.Characteristics> CH_ID Collections.unmodifiableSet(EnumSet.of(Collector.Characteristics.IDENTITY_F…