🎁**“我们不必非常聪明才能改变世界。我们只需要比绝大多数人更早地认识到问题，并付诸行动。”- 毛里茨·萨克斯**
🏀作者：不能再留遗憾了

📱关于作者：博主正在学习C和Java，目前有些关于leetcode刷题的专栏leetcode刷题，该专栏主要是关于数据结构方面的题目，大家有兴趣可以去看看，后面也会完善Java学习的专栏。
🚗本篇文章的主要内容：这篇文章我将为大家分享什么是堆，以及怎样自己创建堆。

什么是堆

堆（Heap）是一种数据结构，通常可以被视为一棵完全二叉树。在堆中，每个节点都满足一种特殊的条件，即父节点的键值总是大于或等于（小于或等于）任何一个子节点的键值，这被称为堆性质。堆是一种非常常见的数据结构，通常用于实现优先队列等应用程序。常见的堆分为两种，分别是最大堆和最小堆，最大堆的根节点的关键字要比它的每个子节点的关键字都要大；最小堆的根节点的关键字要比它的每个子节点的关键字都要小。

既然堆可以被视为完全二叉树，我们就需要知道：堆可以用数组来实现，在数组中，下标为i的节点的左节点为2i+1，右节点为2i+2，父节点为(i-1)/2向下取整。这个知识对我们创建堆的时候非常关键。

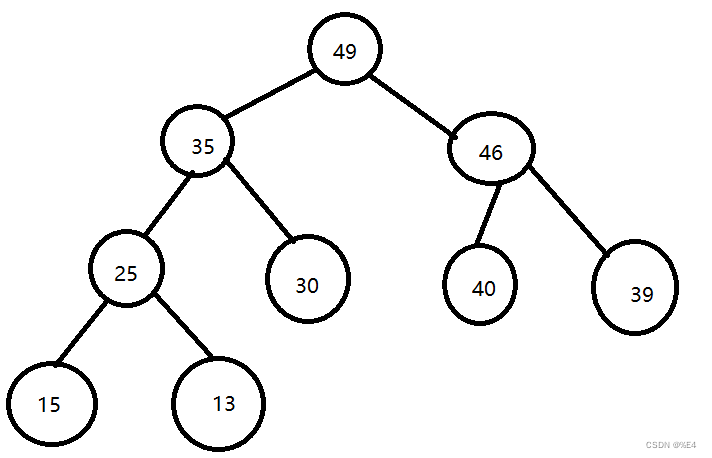
这个就是最大堆，根节点的关键字总是大于子节点的关键字

最小堆，根节点的关键字总是小于子节点的关键字。

如何创建堆

向下调整创建堆

假设给你一个数组{27,15,65,49,37,34,19,18,35}，你需要根据数组里面的数组创建一个最小堆或最小堆。

我们先将数组转换为完全二叉树。

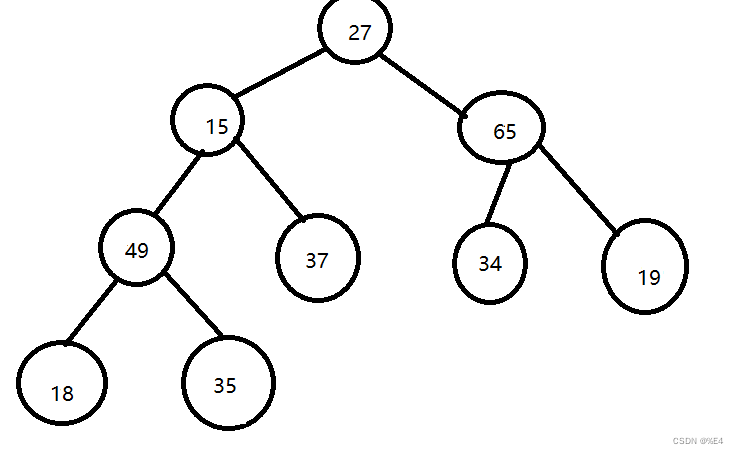
因为提供的数组是随机的，所以我们需要看每一个子树是否符合根节点的关键字大于子节点关键字。我们从二叉树的底部开始创建，将子节点中较大的节点的值与根节点比较，如果子节点的值大于根节点，就将子节点与父节点交换，交换完成后我们需要看子节点所在的子树是否还符合最大堆，所以就需要向下调整。

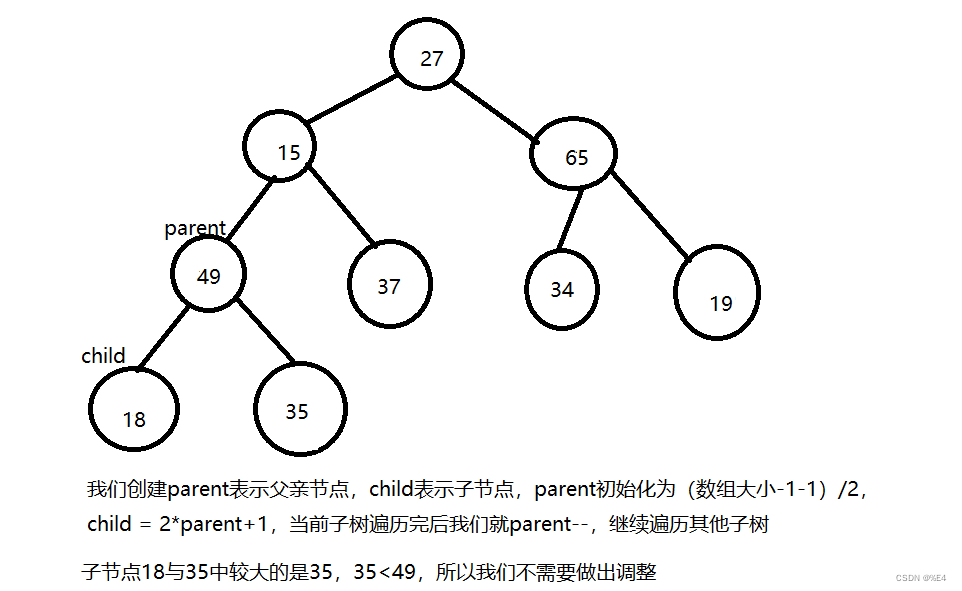
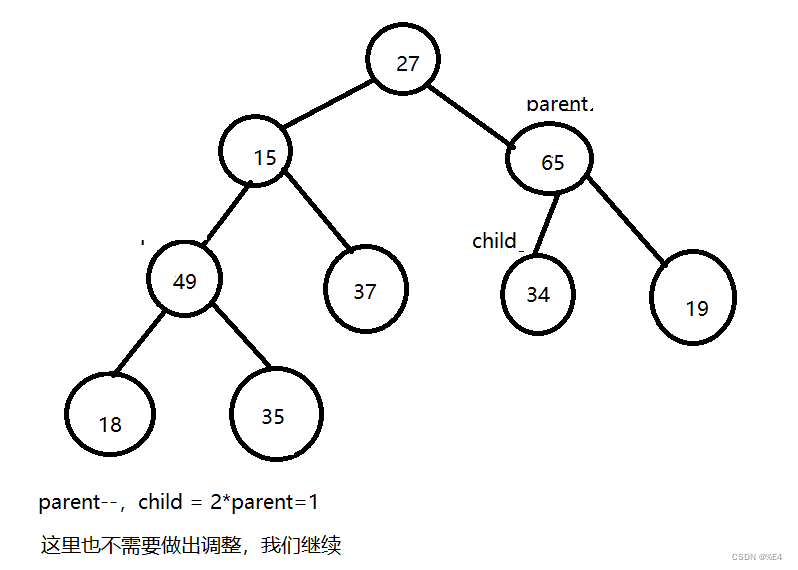
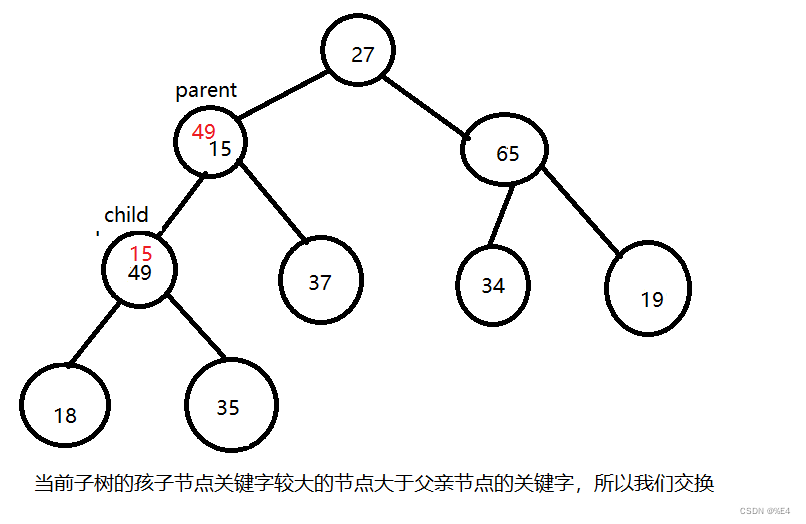
交换之后我们需要判断以15为父亲节点的子树是否符合最大堆




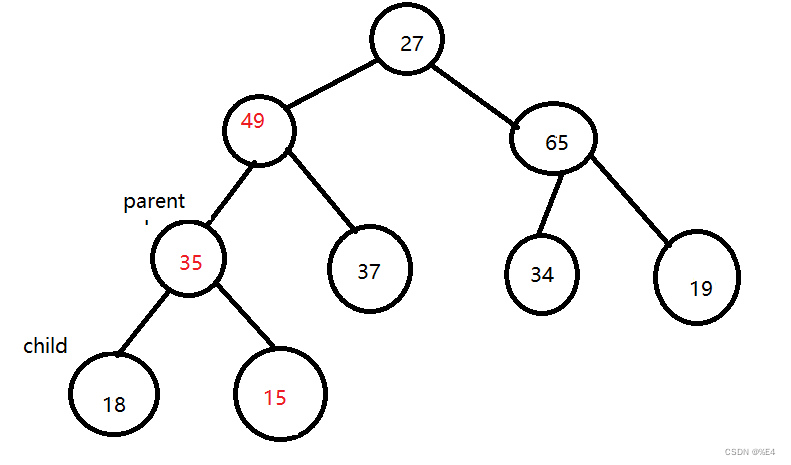
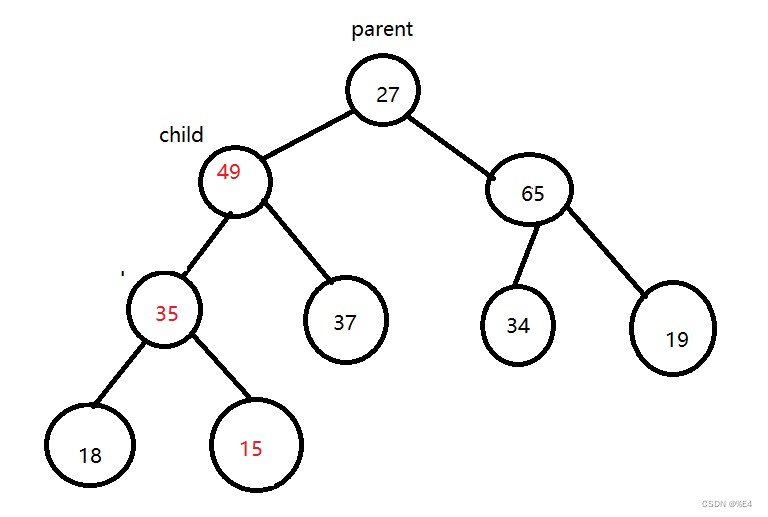
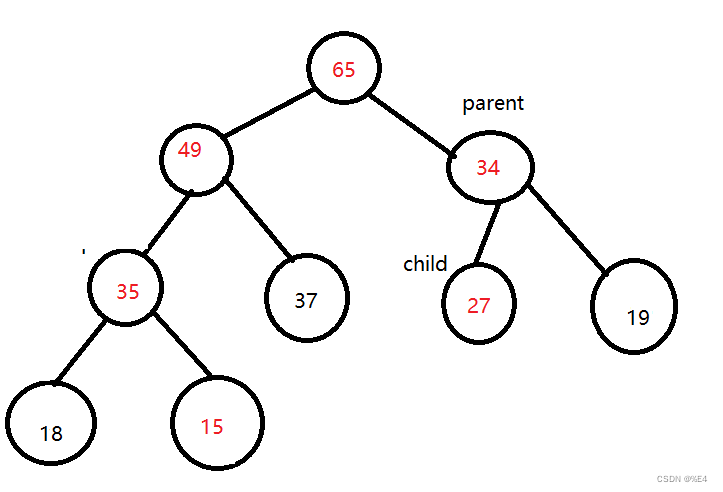
所以我们这个最终的二叉树就是我们需要的最大堆。

看看代码怎么写吧。

public class myHeap {
//因为堆也是数组，所以我们创建一个数组成员变量
    public int[] elem;
    //usedSize用来记录数组的大小
    public int usedSize;
    public myHeap() {
    //假设将数组大小定义为10
        this.elem = new int[10];
    }
    //初始化数组，将传入的数组赋值给elem
    public void initHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[usedSize++] = array[i];
        }
    }

    //创建
    public void creatHeap() {
    //从二叉树的底部开始创建，结束条件是parent = 0
        for (int parent = (usedSize-2)/2; parent >= 0 ; parent--) {
            shiftDown(parent,usedSize);
        }
    }

    private void shiftDown(int parent,int len) {
        int child = 2*parent+1;
        //当child  = len时，说明该子树已遍历完
        while(child < len) {
            if(child+1 < len && elem[child] < elem[child+1]) {
                child++;
            }
            if(elem[parent] < elem[child]) {
                int tmp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = tmp;
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }
}

如果我们像创建最小堆，我们只需要将">“改成”<"就行了。

向上调整创建堆（堆的插入和删除）

如果我们不想你给我一整个数组之后我再创建堆，而是你给我一个数字我就创建堆，那么我们该怎么办呢？这里我们可以使用向上调整的思路来解决，因为我们一个一个添加数字，每次将数字添加在数组的最后，在添加了之后就会调整二叉树，所以就保证了在添加下一个数字之前，你的二叉树就已经满足了最大堆或最小堆，我们添加了一个数字之后就只需要向上做出调整即可。

在删除堆的时候我们默认删除数组的首元素，然后将数组的最后一个元素移动到数组的首地址处。移动之后我们再进行向下调整操作。

同样是这个数组{27,15,65,49,37,34,19,18,35}，我们一个一个添加，看看怎么做吧。

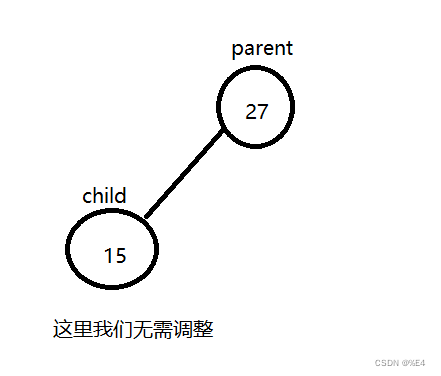
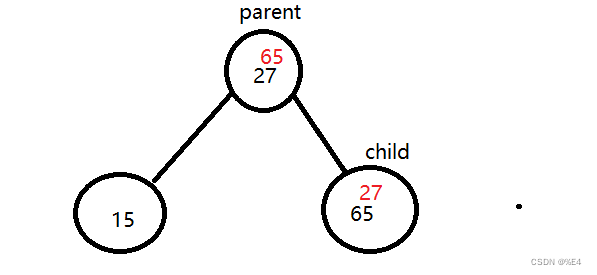
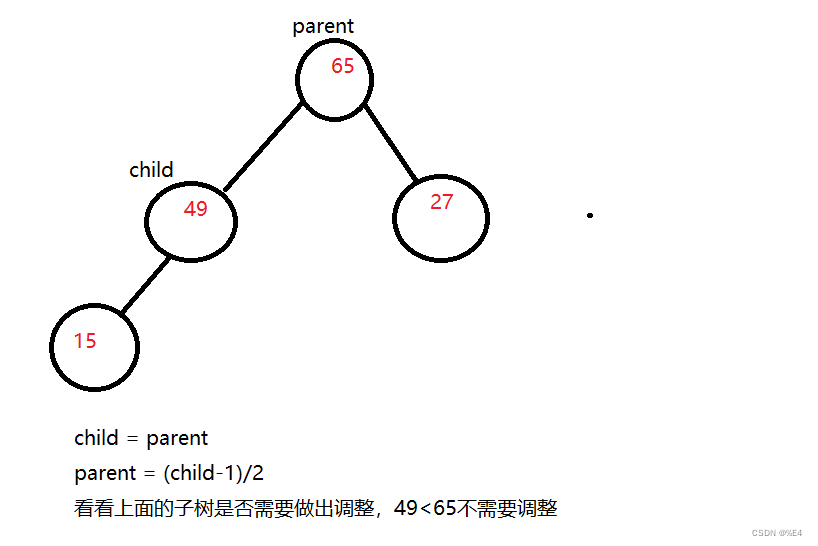
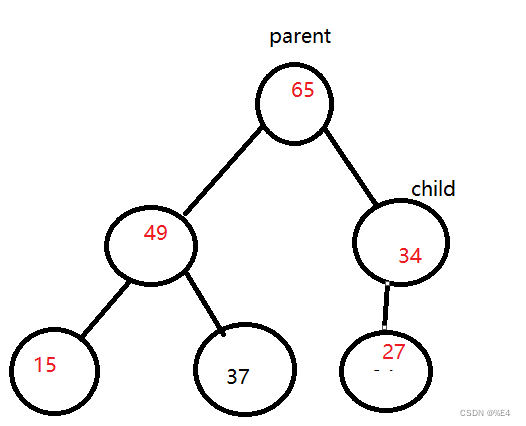
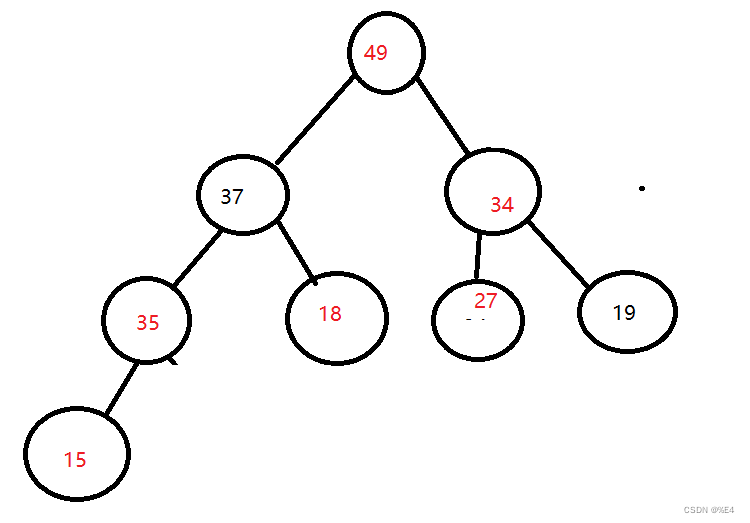
重复此操作



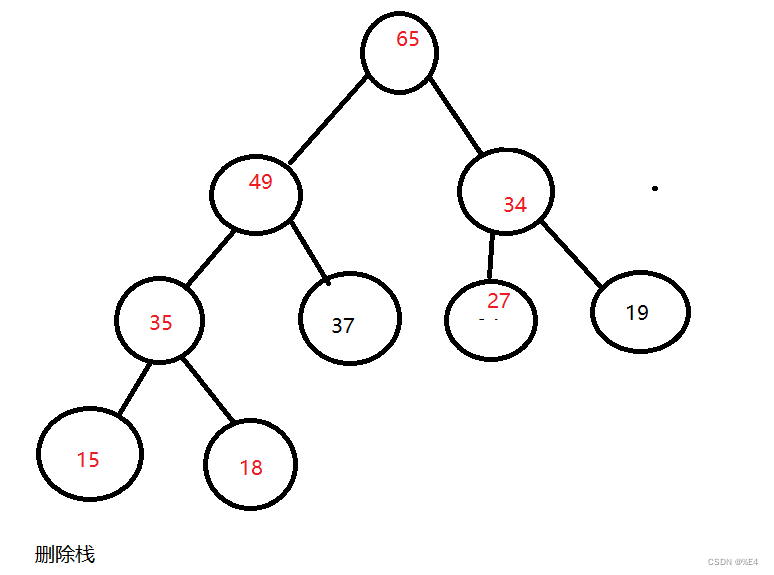
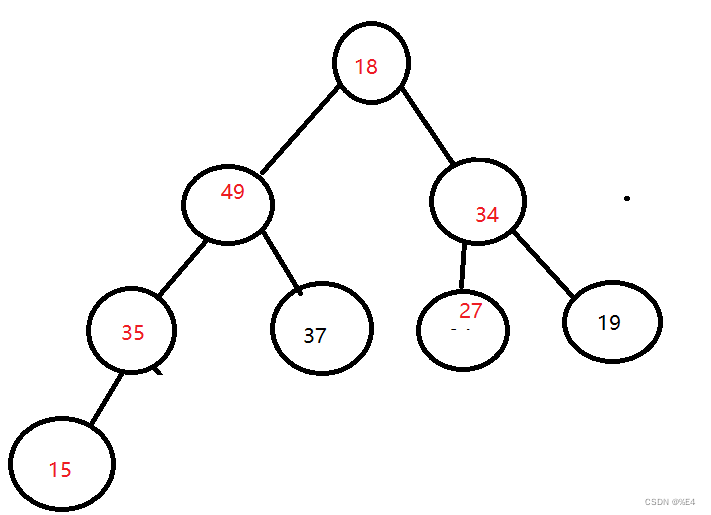
向下调整

public class myHeap {
    public int[] elem;
    public int usedSize;
    public myHeap() {
        this.elem = new int[10];
    }
    
    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while(child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }

    //插入
    public void offer(int data) {
        elem[usedSize++] = data;
        if(isFull()) {
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        shiftUp(usedSize-1);
    }

    public boolean isFull() {
        return usedSize > elem.length;
    }
    //删除操作
    public void pop() {
        if(isEmpty()) {
            return;
        }
        swap(elem,0,usedSize-1);
        usedSize--;
        shiftDown(0,usedSize);
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

    public void swap(int[] array, int i, int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
}