最长公共子序列
- 动态规划算法思想
- 最长公共子序列
- 题目
- 最优解结构性质
- 递归方程
- 递归实现
- 核心函数
- 测试
- 测试结果
- 非递归实现(画表)
- 核心函数
- 测试
- 测试结果
- 求出具体的子序列
动态规划算法思想
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题﹐即将大规模变成小规模,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是﹐适合于用动态规划法求解的问题,经分解得到的子问题往往不是互相独立的。他们之间有关系,所以用一个表来记录所有已解决的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填人表(可以是二维,一维数组,或者是变量)中。这就是动态规划法的基本思想。
最长公共子序列
题目
给定两个序列,返回这两个序列的最长公共子序列的长度。
一个序列的子序列是指这样一个新的序列:它是由原序列在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新序列。
两个序列的公共子序列是这两个序列所共同拥有的子序列。
最长公共子序列问题:给定两个序列X={x1,x2,…xm}和Y={ y1,y2,…yn},找出X和Y的最长公共子序列。
动态规划算法可有效地解此问题。下面按照动态规划算法设计的各个 步骤设计解此问题的有效算法。
最优解结构性质
我们假设Z是X和Y的最长公共子序列,该假设的目的是使该问题的规模不断缩小
最优解结构性质
X={x1,x2,...xm} m
Y={y1,y2,...yn} n
Z={z1,z2,...zk} k
三种情况
- xm== yn==zk
- Zk-1=> Xm-1:Yn-1
- xm!=yn && zk!=xm
- Zk=>Xm-1:Yn
- xm!=yn && zk!=yn
- Zk=>Xm:Yn-1
c[i][j] =>k:
i是X序列的长度,j是Y序列的长度,c代表序列X有i个元素时,序列Y有j个元素时,最长的公共子序列的长度
注意:i不是点值,i是区域值,从1 2到i,j不是点值,j是区域值,从1 2到j
递归方程
分治策略的核心,规模减小到0,如果最后一个值相等,就减小一个规模,如果不相等,有一个max的概念,c[i][j]=c[i-1][j-1]+1可以写成c[i-1][j-1]=c[i][j]-1更好理解,减小规模
- i == 0 || j ==0
- c[i][j]=0
- i>0&&j>0 x[i]==y[j]
- c[i][j]=c[i-1][j-1]+1
- i>0&&j>0 x[i]!=y[j]
- c[i][j]=max(c[i-1][j],c[i][j-1])
所以递归方程为
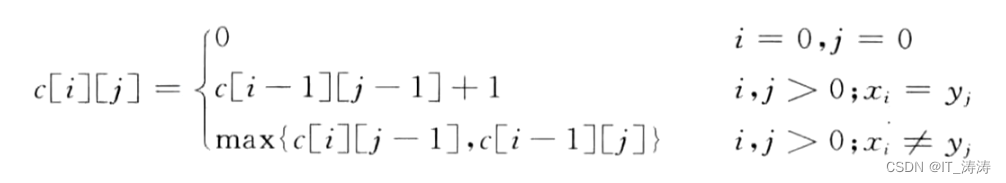
递归实现
核心函数
int sum = 0;
int LCSLength(const char* X, const char* Y, int i, int j) {
sum += 1;
if (i == 0 || j == 0)return 0;
if (X[i] == Y[j]) {
return LCSLength(X, Y, i - 1, j - 1) + 1;
}
else {
int xs = LCSLength(X, Y, i - 1, j);
int ys = LCSLength(X, Y, i, j - 1);
if (xs >= ys)return xs;
else return ys;
}
}
测试
#include<iostream>
#include<vector>
using namespace std;
int main() {
const char* X = { "#ABCBDAB" };
const char* Y = { "#BDCABA" };
int xm = strlen(X) - 1;
int yn = strlen(Y) - 1;
int maxlen = LCSLength(X, Y, xm, yn);
cout << maxlen << endl;
cout << sum << endl;
return 0;
}
测试结果
该函数递归调用次数152,指数增长
非递归实现(画表)
核心函数
所以用填表的方法,先初始化第一行和第一列,然后一行一行的填表,每一行的填写依赖上一行
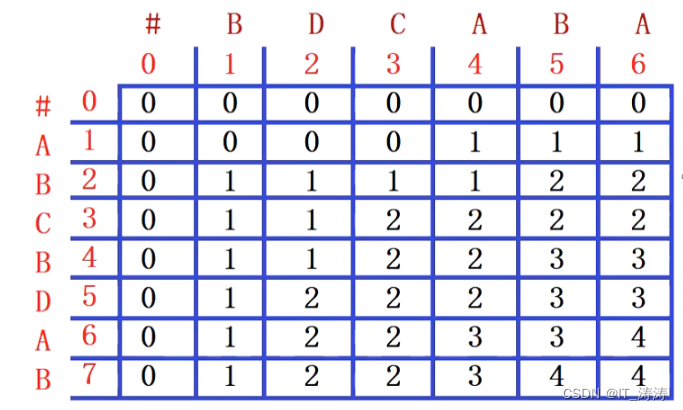
int NiceLCSLength(const char* X, const char* Y, int m, int n, vector<vector<int> >& c) {
for (int i = 0; i <= m; i++)c[i][0] = 0;
for (int i = 0; i <= n; i++)c[0][i] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (X[i] == Y[j]) {
c[i][j] = c[i - 1][j - 1] + 1;
}else if (c[i - 1][j] >= c[i][j - 1]) {
c[i][j] = c[i - 1][j];
}else{
c[i][j] = c[i][j - 1];
}
}
}
return c[m][n];
}
测试
#include<iostream>
#include<vector>
using namespace std;
void PrintVector(vector<vector<int> >& c) {
int m = c.size();
for (int i = 0; i < m;i++) {
for (int j = 0;j<c[i].size();j++) {
printf("%5d", c[i][j]);
}
printf("\n");
}
}
int NiceLCSLength(const char* X, const char* Y, int m, int n, vector<vector<int> >& c) {
for (int i = 0; i <= m; i++)c[i][0] = 0;
for (int i = 0; i <= n; i++)c[0][i] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (X[i] == Y[j]) {
c[i][j] = c[i - 1][j - 1] + 1;
}else if (c[i - 1][j] >= c[i][j - 1]) {
c[i][j] = c[i - 1][j];
}else{
c[i][j] = c[i][j - 1];
}
}
}
return c[m][n];
}
int main() {
const char* X = { "#ABCBDAB" };
const char* Y = { "#BDCABA" };
int xm = strlen(X) - 1;
int yn = strlen(Y) - 1;
vector<vector<int> >c(xm + 1, vector<int>(yn + 1,0));
int maxlen = NiceLCSLength(X, Y, xm, yn,c);
cout << maxlen << endl;
PrintVector(c);
return 0;
}
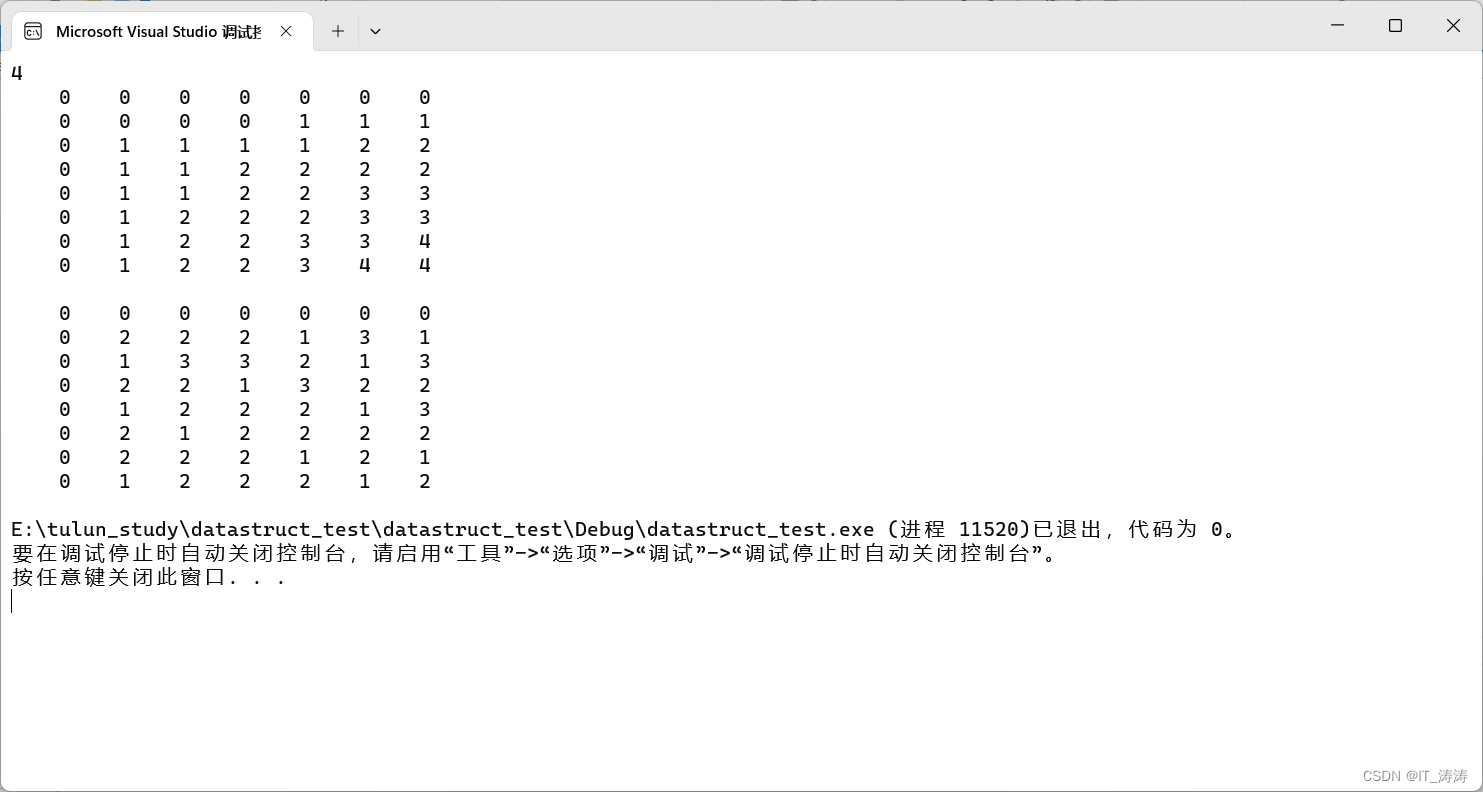
测试结果
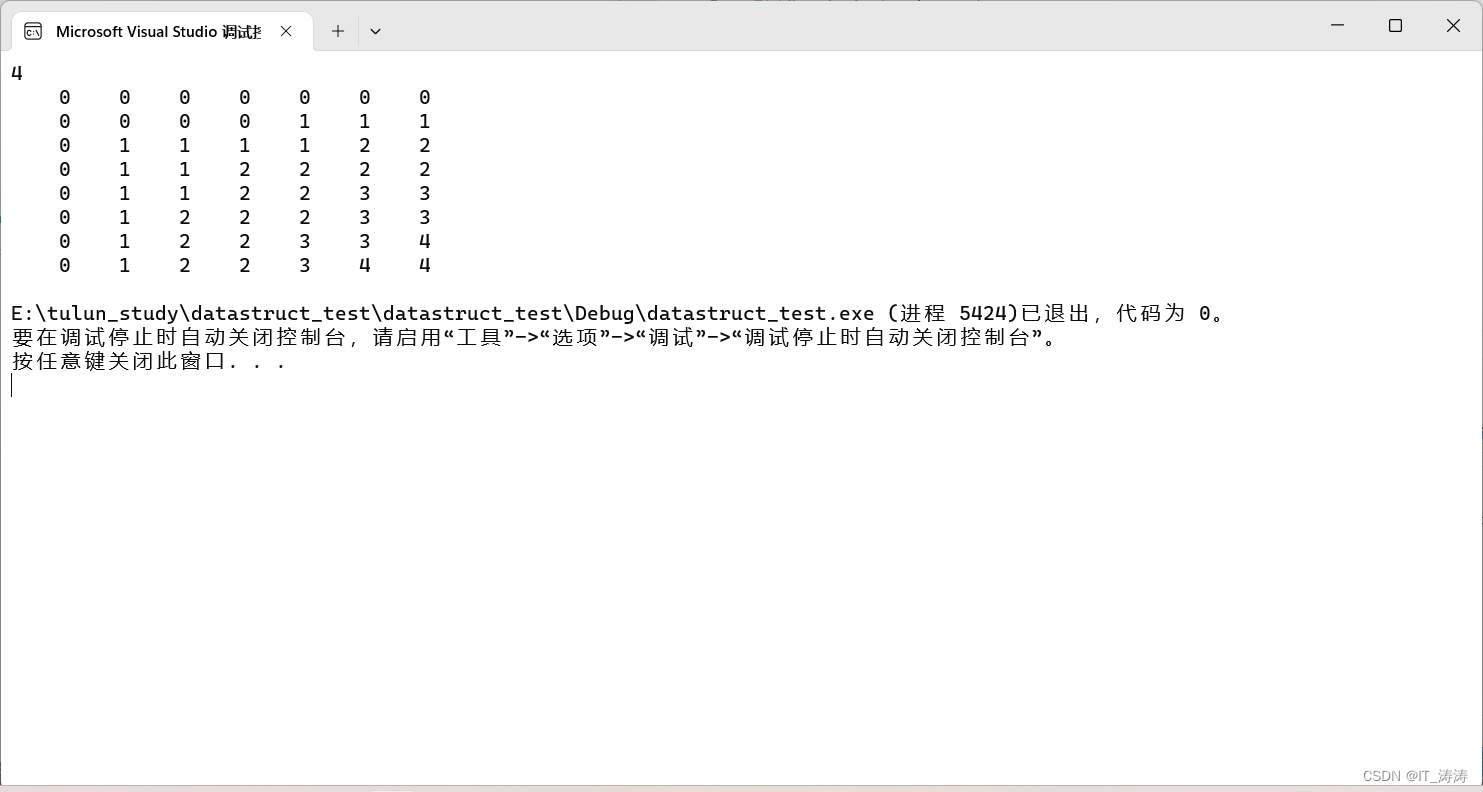
求出具体的子序列
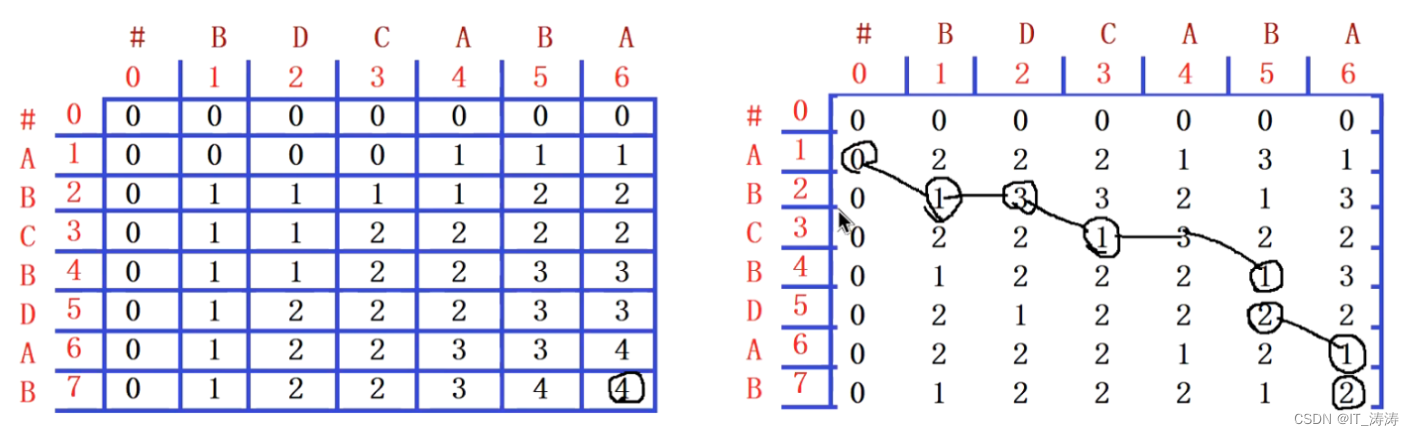
对于如何将具体的最长公共子序列求出来呢
我们再定义一个二维数组,记录2是行减一,3是列减一,1是行列都减一
int NiceLCSLength(const char* X, const char* Y, int m, int n, vector<vector<int> >& c, vector<vector<int> >& s) {
for (int i = 0; i <= m; i++)c[i][0] = 0;
for (int i = 0; i <= n; i++)c[0][i] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (X[i] == Y[j]) {
c[i][j] = c[i - 1][j - 1] + 1;
s[i][j] = 1;
}
else if (c[i - 1][j] >= c[i][j - 1]) {
c[i][j] = c[i - 1][j];
s[i][j] = 2;
}else{
c[i][j] = c[i][j - 1];
s[i][j] = 3;
}
}
}
return c[m][n];
}
void LCS(int i, int j, const char* X, vector<vector<int> >& s) {
if (i == 0 || j == 0)return;
if (s[i][j] == 1) {
LCS(i - 1, j - 1, X, s);
printf("%5c", X[i]);
}
else if (s[i][j] == 2) {
LCS(i - 1, j, X, s);
}
else {
LCS(i, j - 1, X, s);
}
}