300.最长递增子序列

想清楚如何推导dp数组是关键

两层for循环，因为递增序列不是连续的

• 题目链接：代码随想录

• 解题思路：
  1.dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
  2.状态转移方程：位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
  3.dp[i]的初始化：每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1
  4.遍历顺序
  dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来，那么遍历i一定是从前向后遍历。
  j其实就是遍历0到i-1，那么是从前到后，还是从后到前遍历都无所谓，只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯从前向后遍历。

• 推导过程

  

public int lengthOfLIS(int[] nums) {
    //1.定义dp数组
    int[] dp = new int[nums.length];

    //2.初始化dp数组
    Arrays.fill(dp, 1);

    int result = 1;

    //3.遍历
    for (int i = 1; i < nums.length; i++) {

        //第二层for循环用于更新dp的值
        for (int j = 0; j < i; j++) {
            if(nums[j] < nums[i]){
                dp[i] = Math.max(dp[j] + 1, dp[i]);//不断更新dp[i]
            }
        }

        result = Math.max(result, dp[i]);
    }

    return result;
}

674. 最长连续递增序列

不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关

• 题目链接：代码随想录

• 解题思路：

  本题与上一题的区别：
  ①公式：dp[i] = dp[i - 1] + 1;
  ②遍历形式：本题要求连续递增子序列，所以就只要比较nums[i]与nums[i - 1]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。
  既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i] 和 nums[i - 1]。

• 推导过程：

  

public int findLengthOfLCIS(int[] nums) {

    if(nums.length == 0){
        return 0;
    }
    //1.dp数组
    int[] dp = new int[nums.length];

    //2.初始化
    Arrays.fill(dp, 1);

    int result = 1;

    //3.遍历
    //注意这里是一层for循环遍历
    for (int i = 1; i < dp.length; i++) {
        if(nums[i] > nums[i - 1]){
            dp[i] = Math.max(dp[i], dp[i - 1] + 1);//更新dp数组
        }

        if(result < dp[i]){
            result = Math.max(result, dp[i]);
        }
    }

    return result;
}

//贪心：
// public int findLengthOfLCIS(int[] nums) {

//     if (nums.length == 0) return 0;
//     int res = 1; // 连续子序列最少也是1
//     int count = 1;
//     for (int i = 0; i < nums.length - 1; i++) {
//         if (nums[i + 1] > nums[i]) { // 连续记录
//             count++;
//         } else { // 不连续，count从头开始
//             count = 1;
//         }
//         if (count > res) res = count;
//     }
//     return res;
// }

718. 最长重复子数组

1. 暴力解法：只需要先两层for循环确定两个数组起始位置，然后再来一个循环可以是for或者while，来从两个起始位置开始比较，取得重复子数组的长度

2. 本题动态规划就是记录下暴力解法的所有可能性结果下，以某下表结尾的连续子数组的最大长度。记忆状态换时间

• 题目链接：代码随想录

• 解题思路：
  1.dp数组定义：dp(i)[j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp(i)[j]。
  2.递推公式：当A[i - 1] 和B[j - 1]相等的时候，dp(i)[j] = dp(i - 1)[j - 1] + 1;这时由前一个状态推导而来
  3.初始化
  根据dp(i)[j]的定义，dp(i)[0] 和dp(0)[j]其实都是没有意义的！但dp(i)[0] 和dp(0)[j]要初始值，因为
  为了方便递归公式dp(i)[j]= dp(i - 1)[j - 1] + 1;
  举个例子A[0]如果和B[0]相同的话，dp(1)[1] = dp(0)[0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来。

• 推导过程：

  

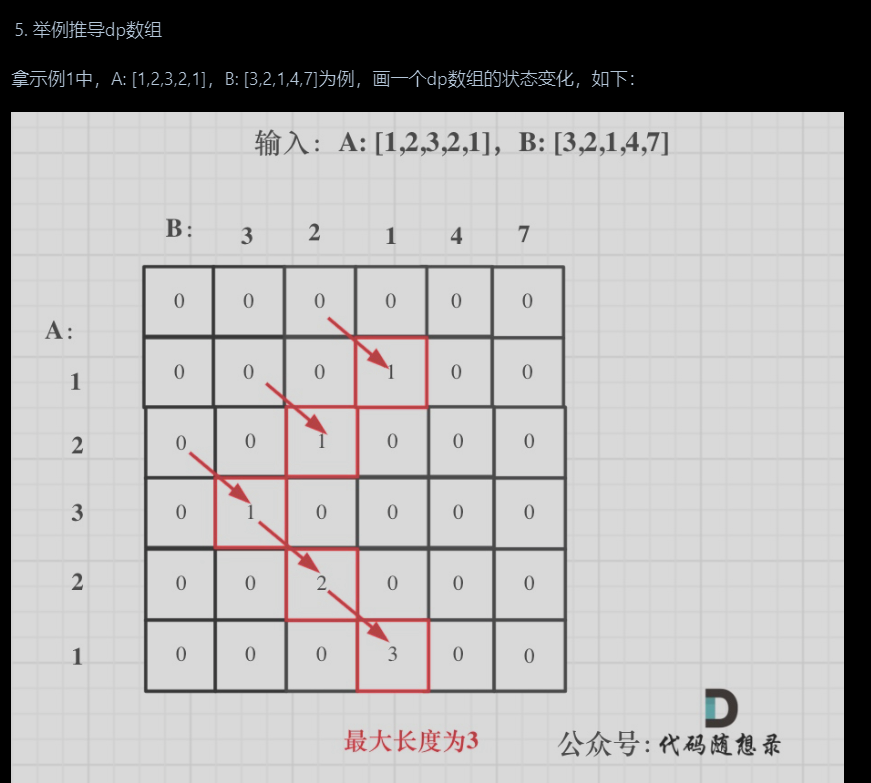
public int findLength(int[] nums1, int[] nums2) {
    //1.定义dp数组
    int[][] dp = new int[nums1.length + 1][nums2.length + 1];//因为dp数组的含义是一i-1下标为结尾的数组的长度
    //2.初始化
    //3.遍历
    int result = 0;

    for (int i = 1; i <= nums1.length; i++) {//i从1开始  nums1数组
        for (int j = 1; j <= nums2.length; j++) {//      nums2数组
            if(nums1[i - 1] == nums2[j - 1]){
                dp[i][j] = dp[i - 1][j - 1] + 1;
                result = Math.max(result, dp[i][j]);
            }
        }
    }

    return result;
}