插入排序介绍

插入排序(Insertion Sort)的基本思想是:
把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

插入排序实现

下面选取直接插入排序的一个中间过程对其进行说明。假设{20,30,40,10,60,50}中的前3个数已经排列过，是有序的了；接下来对10进行排列。示意图如下:

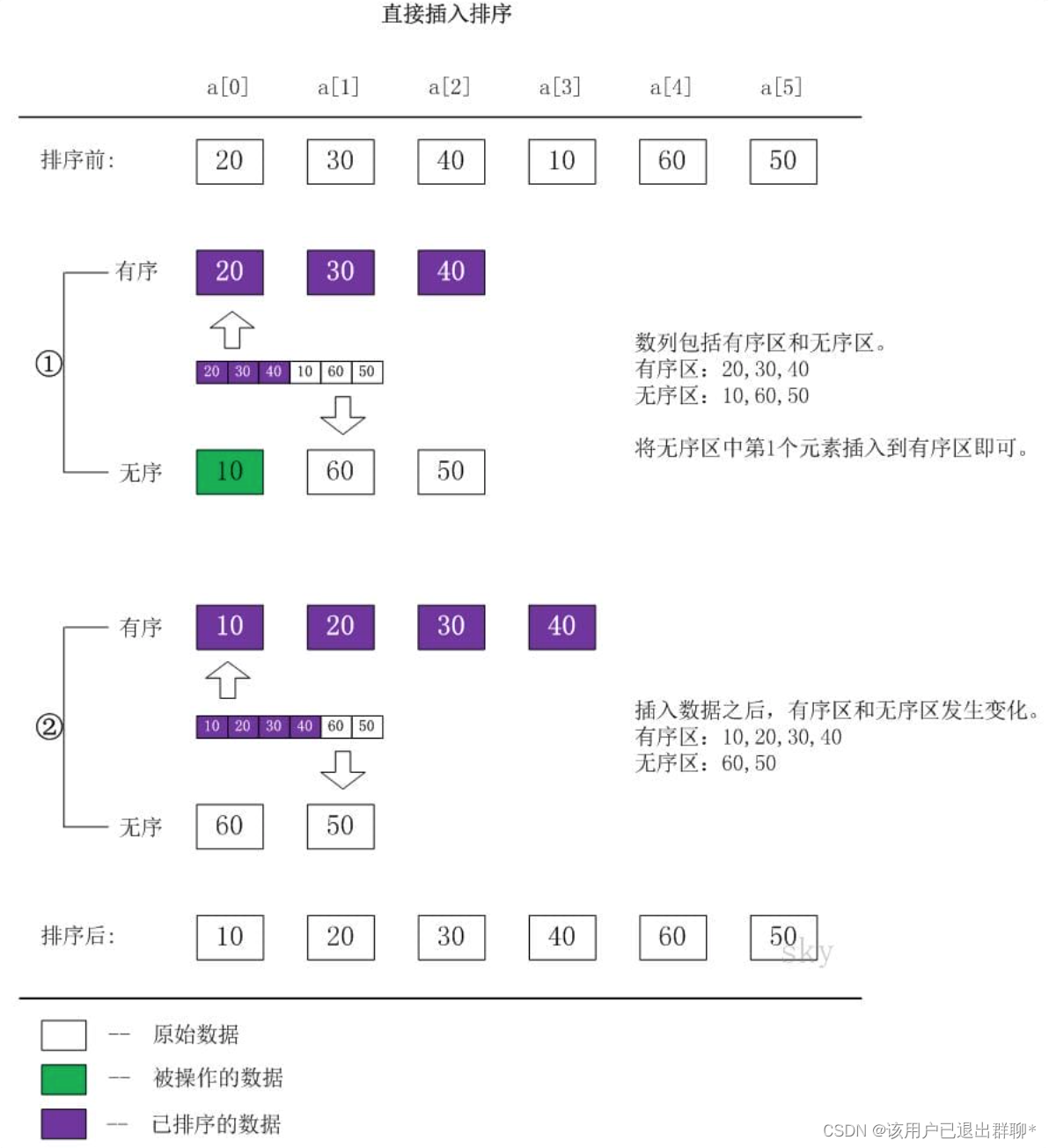
在这里插入图片描述

图中将数列分为有序区和无序区。我们需要做的工作只有两个:

(1)取出无序区中的第1个数，并找出它在有序区对应的位置。
(2)将无序区的数据插入到有序区；若有必要的话，则对有序区中的相关数据进行移位。

插入排序的时间复杂度和稳定性

插入排序时间复杂度

直接插入排序的时间复杂度是O(N2)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? N-1！因此，直接插入排序的时间复杂度是O(N2)。

插入排序稳定性

直接插入排序是稳定的算法，它满足稳定算法的定义。
算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现


package com.zxn;

/**
 * @author zxn
 * @ClassName InsertSort
 * @Description
 * @createTime 2023年04月26日 07:41:00
 */
public class InsertSort {
    public static void insertSort(int[] a, int n) {
        int i, j, k;

        for (i = 1; i < n; i++) {

            //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置
            for (j = i - 1; j >= 0; j--) {
                if (a[j] < a[i]) {
                    break;
                }
            }
            //如找到了一个合适的位置
            if (j != i - 1) {
                //将比a[i]大的数据向后移
                int temp = a[i];
                for (k = i - 1; k > j; k--) {
                    a[k + 1] = a[k];
                }
                //将a[i]放到正确位置上
                a[k + 1] = temp;
            }
        }
    }

    public static void main(String[] args) {
        int i;
        int[] a = {20, 40, 30, 10, 60, 50};

        insertSort(a, a.length);

        System.out.printf("after  sort:{");
        for (i = 0; i < a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
        System.out.println("}");
    }
}