( “图“ 之二分图 ) 785. 判断二分图 —

( “图“ 之二分图 ) 785. 判断二分图 ——【Leetcode每日一题】

news2024/11/18 2:33:59

❓785. 判断二分图

难度：中等

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例 1：

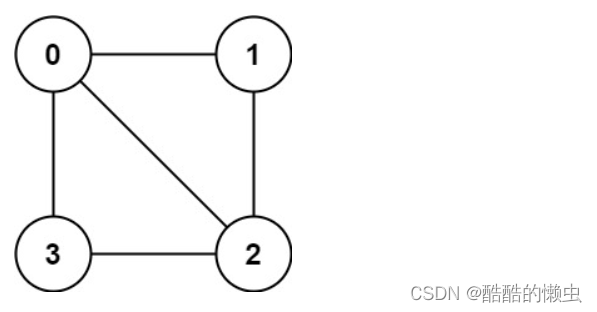
在这里插入图片描述

输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

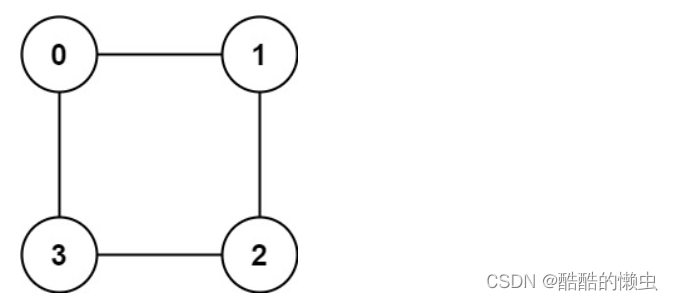
在这里插入图片描述
提示：

graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] 不会包含 u
graph[u] 的所有值互不相同
如果 graph[u] 包含 v，那么 graph[v] 也会包含 u

💡思路：广度优先搜索

由二分图的定义，graph[u]中的所有结点都应该和u在不同的子集，可以将其当作为 边：

可以用两种颜色对图中的节点进行着色，并且保证相邻的节点颜色不同，那么这个图就是二分图，这里为colors数组，分别用 0 和 1 来着色，表示不同的集合；
由于所个图有可能不是连通图，所以要考虑这种情况；
然后对其中一个结点进行广度优先搜索，并对其着色，如果相邻点颜色相同，则不是二分图，返回false。

🍁代码：(Java、C++)

Java

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] colors = new int[graph.length];
        Arrays.fill(colors, -1);
        for (int i = 0; i < graph.length; i++) {  // 处理图不是连通的情况
            if (colors[i] == -1 && !isBipartite(i, 0, colors, graph)) {
                return false;
            }
        }
        return true;
    }
    private boolean isBipartite(int curNode, int curColor, int[] colors, int[][] graph) {
        Stack<Integer> stk = new Stack<>();
        stk.push(curNode);
        colors[curNode] = curColor;
        while(!stk.empty()){
            curNode = stk.pop();
            curColor = colors[curNode];
            for(int nextNode : graph[curNode]){
                if(colors[nextNode] != -1 && colors[nextNode] == curColor){
                    return false;
                }else if(colors[nextNode] == -1){
                    colors[nextNode] = 1 - curColor;
                    stk.push(nextNode);
                }
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        vector<int> colors(graph.size(), -1);
        for(int i = 0; i < graph.size(); i++){//处理图不连通的情况
            if(colors[i] == -1 && !isBipart(i, 0, colors, graph)){
                return false;
            }
        }
        return true;
    }
    bool isBipart(int curNode, int curColor, vector<int>& colors, vector<vector<int>>& graph) {
        stack<int> stk;
        stk.push(curNode);
        colors[curNode] = curColor;
        while(!stk.empty()){
            curNode = stk.top();
            stk.pop();
            curColor = colors[curNode];
            for(int nextNode : graph[curNode]){
                if(colors[nextNode] != -1 && colors[nextNode] == curColor){
                    return false;
                }else if(colors[nextNode] == -1){
                    colors[nextNode] = 1 - curColor;
                    stk.push(nextNode);
                }
            }
        }
        return true;
    }
};